Млекоченко Николай Федорович. Несмотрнте

Оптические свойства периодической среды описываются тензорами диэлектрической проницаемости и восприимчивости, которые вследствие трансляционной симметрии среды являются периодическими функциями координаты х:

е(х) = е(х + а), м(х) = ц(х + а),где а -- любой произвольный вектор решетки. Эти формулы отражают лишь то, что наблюдатель, расположенный в точке х, "видит" среду такой же, как и наблюдатель в точке х + а. В случае трехмерной периодической среды, такой, как кристалл, периодичность решетки определяется элементарными векторами а,, а₂ и а₃. Среда остается инвариантной относительно перемещения на любой вектор а, представляющего собой сумму целого числа этих векторов.

Распространение монохроматического (с частотой а>) лазерного излучения в периодической среде описывается уравнениями Максвелла

-- X Н = шеЕ, (6.1.2)

-- X Е = - ш/хН . (6.1.3)

Эти уравнения должны оставаться неизменными, если в оператор

-- и е, ц вместо х подставить х + а. Трансляционная симметрия среды позволяет выбрать нормальные моды в виде

Е = Е_к(х)е-'^к-,

Н = Н_к(х)е *,

где Е_к(х) и Н_к(х) -- периодические функции, т. е.

Е_к(х) = Е_к(х + а),

Н_к(х) = Н_к(х + а).

Это свойство известно как теорема Флоке (или Блоха) и будет доказано ниже. Нижний индекс К указывает на то, что функции Е_к и Н_к зависят от вектора К, который называется блоховским волновым вектором. Величины со и К связаны дисперсионным уравнением

" = "(К). (6.1.6)

В случае когда периодичность исчезает, функции Е_к(х) и Н_к(х) становятся не зависящими от х, а нормальные моды -- плоскими волнами с волновым вектором, равным блоховскому. Наша основная цель состоит в определении Е_к(х), Н_к(х) и нахождении дисперсионной зависимости со (К).

6.1.1. ОДНОМЕРНЫЕ ПЕРИОДИЧЕСКИЕ СРЕДЫ

В современной оптике часто приходится иметь дело с одномерной периодической средой, тензор диэлектрической проницаемости которой г. удовлетворяет условию

е{г) = е{г + /Л), (6.1.7)

где Л -- период, а / -- некоторое целое число. В данной главе мы ограничимся рассмотрением распространения лазерного излучения в одномерной периодической немагнитной среде. На рис. 6.1 показана типичная периодическая среда, представляющая собой чередующиеся слои двух прозрачных материалов. Предположим, что на

0x01 graphic

РИС. 6.1. Типичная периодическая слоистая среда, состоящая из чередующихся слоев ваА^ и А1 ва, А.5, выращенных на подложке из ваАз методом эпитаксии из молекулярных пучков [7].

эту периодическую слоистую среду падает пучок лазерного излучения. Свет будет претерпевать отражение и преломление на каждой границе раздела. Пусть в -- угол падения. Интерференционные максимумы при отражении возникают при условии

2Ксо&в = т\ , (6.1.8)

которое называется условием Брэгга. Его легко вывести, сравнивая разность фаз между лучами, отраженными от последовательных плоскостей решетки. Конструктивная интерференция возникает, когда оптическая разность фаз между лучами, отраженными от последовательных плоскостей решетки, составляет целое число длин волн. Распространение электромагнитного излучения в таких средах подчиняется волновому уравнению

V X (V X Е) - <о²/хе^ё = 0- (6.1.9)

Поскольку среда является периодической, диэлектрический тензор ё можно разложить в ряд Фурье:

"(*) = ёес"~'^С"^х, (6.1.10)

где в пробегает все векторы обратной решетки, включая С = 0. В нашем одномерном случае

^{С = /8 = /}Т²' ^/= Ђ1,+2, Ђ3,..., (6.1.11)

^е(²) = Т,е,е-"^(2,г/А)2.

В физике твердого тела вектор в называется вектором обратной решетки. В физике кристаллов этот вектор играет фундаментальную роль. В одномерной периодической среде вектор § параллелен оси г. Вектор электрического поля в этой периодической среде в общем случае можно выразить через интеграл Фурье:

Е = 1<1³кА(к)е-'^к-*. (6.1.12)

Подставляя выражения (6.1.12) и (6.1.10) в (6.1.9), получаем х [к х А(к)]+ <о²/хёА(к - = 0.

Это условие выполняется только тогда, когда все множители при _е-/к-х обращаются в нуль. Таким образом,

k X [к X А(к)] + <o²/x?e_GA(k - G) = 0 для любого к, (6.1.13)

где суммирование производится по всем векторам обратной решетки. Это условие представляет собой бесконечную однородную систему уравнений относительно неизвестных коэффициентов А(к). Каждое уравнение в этой системе имеет свое, отличное от другого значение к. В принципе для этой системы можно решить характеристическое уравнение, получаемое приравниванием детерминанта системы уравнений (6.1.13) нулю. Однако при более внимательном рассмотрении системы (6.1.13) можно заметить, что не все коэффициенты А(к) связаны между собой. Оказывается, что связаны только коэффициенты вида A(k - G). Это позволяет разбить полную систему уравнений (6.1.13) на много подсистем, каждая из которых относится к волновому вектору К и содержит уравнения относительно А(К) и А(К -- G) со всевозможными векторами G. Каждая такая подсистема может быть решена по отдельности. Используя это свойство для системы (6.1.13), решение подсистемы, характеризуемой вектором К, можно записать в виде

Е_к = 1>(К - GK'<^k-^g>- = G

= <>-'^к-'ХА(К - G)e'^G-' = (6.1.14)

= е~'^к'^гЕ_к(г).

В одномерном случае G = /g - 12-wi/A.. Поэтому

Е_к(г) = ёА(К - /gy^/A); (6.1.15)

является периодической функцией с периодом Л. Выражение (6.1.14) определяет нормальную моду распространения. Более общее решение (6.1.12) теперь представляет собой линейную суперпозицию этих нормальных мод. Тем самым мы доказали теорему (6.1.5).

При условии что частота w задана, из уравнений (6.1.13) можно получить волновой вектор К. Если среда однородна в х- и ^-направлениях, т. е. ё не зависит от х и у, то из (6.1.14) и (6.1.15) находим следующее выражение для блоховской моды электрического поля:

Е - _е-цк_хх+к_уУ)_е-и<_ггЕ_к(г), (6.1.16)

где Е_к(г) -- периодическая функция от г. В этом случае, задавая частоту оз и набор величин (К_х, К_у), из уравнений (6.1.13) можно определить K_z. Существуют области значений оз, для которых К. становится комплексным числом, и, следовательно, блоховская волна (6.1.16) оказывается затухающей. Падающее излучение от этих областей будет полностью отражаться. В диапазоне рентгеновского излучения это явление называется брэгговским отражением. Поскольку наибольший интерес представляют явления и устройства, использующие периодические среды в области их запрещенных зон, мы будем искать приближенные решения для блоховских волн, когда условие Брэгга приблизительно выполняется. Чтобы проиллюстрировать основные идеи, для простоты в дальнейшем будем предполагать, что волна распространяется в направлении г (т. е. К_х = К_у - 0) и что вектор поля перпендикулярен волновому вектору (К-Е = 0). Кроме того, будем предполагать среду изотропной, т. е. считать, что ё/ является скалярной величиной. При этом система уравнений (6.1.13) принимает вид

к²А(к) - и²ц^₁е,А(к - = 0. (6.1.17)

Для нахождения блоховской волны с волновым числом К (здесь для простоты опущен нижний индекс г) требуется решить систему уравнений (6.1.17) с к = К, К Ђ g, К Ђ 2$, ... . Поскольку мы снова имеем бесконечное число уравнений относительно А (К), А (К Ђ Ђ g), А (К Ђ 2$), ... , для получения явного решения требуется сделать еще одно приближение. Чтобы это приближение было корректным, нужно исследовать все входящие в уравнения члены и пренебречь малыми величинами. Записывая в (6.1.17) несколько первых членов для к - К, получаем уравнение

К²А(К) - и²це₀А{К) - <л²це_{А(К - ₈) - и^^К + я) =-0,

(6.1.18)

которое можно также переписать в виде

^А(^К) = ¹ 2 - 8) + ^е__хА(К+ ")+""•].

К - и це₀

Аналогично, уравнение (6.1.17) для k = K- guk = K + g можно записать соответственно в виде

A(K-g) = ~[и²ц_е1А(К - 2g) + _и²^__хА{К) +•••],

(К- g) - "v₀

(6.1.20)

_А(_К + _g) = J ₊_u2_fie__{iA(K+ 2g})+...].

(K+g) - "Vо

(6.1.21)

Из уравнений (6.1.19) -- (6.1.21) следует, что если \K-g\tsK, (6.1.22)

К² = (6.1.23)

то основными членами являются А (К) и А{К -- g). Физически это означает, что между составляющими плоских волн А (К) и А (К --

-- g) имеется резонансная связь. Пренебрегая всеми другими коэффициентами, систему уравнений (6.1.17) для блоховских волн с волновым числом К можно переписать в виде

(а:² - ы²це₀)А(К) - ы²ЦЕ\А{К - g) = 0, (6.1.24)

-- + [(* - gf - ы²це₀]А(К -g) = 0. (6.1.25)

Заметим, что е₀ здесь представляет нулевую фурье-компоненту диэлектрического тензора, а = е*, если е-- вещественная диэлектрическая функция.

Уравнения (6.1.24) и (6.1.25) представляют собой систему линейных уравнений для амплитуд поля А (К) и А (К -- g). Она имеет нетривиальное решение только в случае, когда детерминант системы равен нулю:

(6.1.26)

= о,

К² - и²це₀ -и>^гце_{

-w²/xe_, (К- g)² - и²це₀

или

(6.1.27)

(К² - ^e₀)[(K-g)² - "V₀] - (<oV|_e,|)² = о.

Последнее уравнение представляет собой явную запись дисперсионного уравнения (6.1.6), определяющего зависимость ы(К). Условие

Брэгга (6.1.22) точно выполняется при К = (1/2)# = 7г/Л. При этом значении К из уравнения (6.1.27) получаем следующие два корня со²:

Эти корни определяют границы спектральной полосы. При частотах со между со₊ и со_ корни уравнения (6.1.27) для К являются комплексными числами, вещественная часть которых равна -к/К. Волны при этом являются затухающими, а их спектральный диапазон называется "запрещенной зоной".

При частотах со, лежащих вне этой запрещенной зоны, корни уравнения (6.1.27) для К являются вещественными и решения отвечают распространяющимся волнам. Уравнение (6.1.27), устанавливающее связь между со и А', называется дисперсионным. На рис. 6.2 представлено графическое изображение дисперсионного уравнения (6.1.27) для типичной периодической среды. Для трехмерной периодической среды дисперсионное уравнение (6.1.6) соответствует поверхностям постоянной частоты в К-пространстве. В случае трехмерных периодических сред могут также существовать запрещенные зоны частот со. Волны с частотами в запрещенных зонах не могут распространяться, поскольку вследствие брэгговского отражения они затухают. Это нетрудно показать, если вычислить волновое число К в центре запрещенной зоны при со² = (#/2[см. (6.1.22) и (6.1.23)] и К = + х, где 1x1 #/2. При этом дисперсионное уравнение (6.1.27) принимает вид

(6.1.29)

где мы пренебрегли числом, пропорциональным X⁴. Из уравнения (6.1.29) можно найти волновое число К в центре запрещенной зоны:

(6.1.30)

Поскольку это волновое число является комплексным, оно отвечает экспоненциально затухающей амплитуде. Следует отметить, что это пространственное затухание существенно зависит от коэффициента ё, в фурье-разложении. Ширина запрещенной зоны определяется величиной Дсо_вар = 1со₊ -- со_ I и в соответствии с (6.1.28) дается выражением

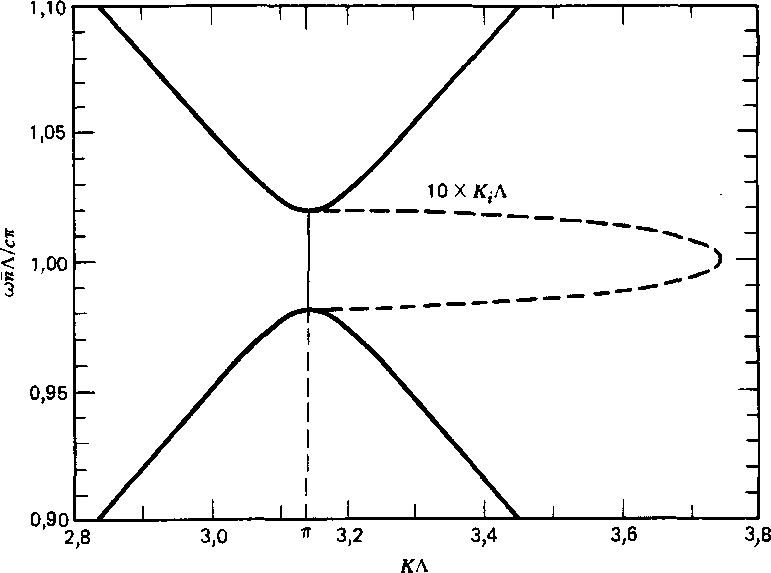
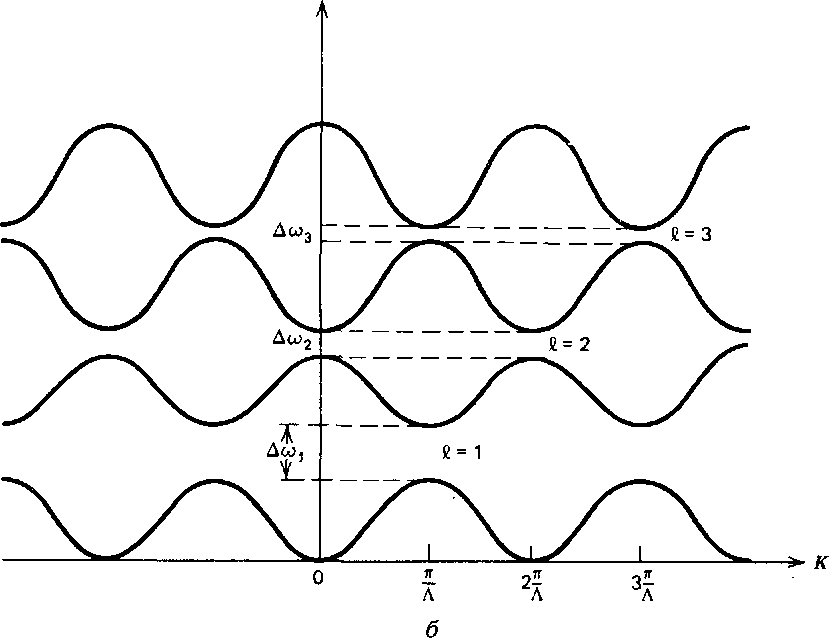
0x01 graphic

12-631

О!

0x01 graphic

РИС. 6.2. а -- дисперсионная кривая в области запрещенной зоны для периодической структуры, изображенной на рис. 6.3 при л₁ = 3,2, п₂ = 3,4, а = Ь = 0,5Л; заметим, что К становится комплексным, когда Яе(А'Л) = 7г; б "-- общий вид дисперсионных кривых ш(К) для основной запрещенной зоны (/ = 1) и запрещенных зон высшего порядка (/ = 2, 3).

Таким образом, ширина запрещенной зоны Ди пропорциональна коэффициенту Фурье для диэлектрической Проницаемости. Из выражений (6.1.30) и (6.1.31) можно заметить, что мнимая часть волнового числа в центре запрещенной зоны пропорциональна относительной ширине этой зоны (Ли /со) и дается выражением

К^и--^, (6.1.32)

где, как мы помним, g = 2тг/Л.

Выше при получении формул мы предполагали, что распространение волн происходит в направлении периодического изменения диэлектрической проницаемости", т. е. вдоль оси г. Для произвольного направления распространения (т. е. когда К_х или К_у ^ 0) дисперсионное уравнение оказывается более сложным и зависит от состояния поляризации. Это будет показано в следующем разделе при исследовании распространения волн в периодических слоистых средах.

При выводе дисперсионного уравнения (6.1.27) мы предполагали IК -- g I = К [соотношение (6.1.22)] и К² ~ а>²це₀ [соотношение (6.1.23)], что следует из условия резонансной связи между коэффициентами А (К) и А (К - g). Запрещенная зона, связанная с брэггов- ским условием (6.1.22), определяется коэффициентом фурье-разло- жения ё; диэлектрической функции Е(г). В общем случае существует запрещенная зона, связанная с каждым коэффициентом Фурье е, диэлектрической функции ё(г). Для иллюстрации этого рассмотрим случай, когда

\K-lg\~K, /=Ђ1,Ђ2,..., (6.1.33)

К² = и²це₀. (6.1.34)

Аналогично тому как были выведены уравнения (6.1.24) и (6.1.25), можно получить

(К² - ш²^ё₀)А(К) - и²₁1е,А(К - = 0, (6.1.35)

-и²^_,Л(К) + [(К - 1е)² ~ ^е₀]А(К - ^ 0. (6.1.36)

Это приводит к запрещенной зоне при

г*

Поскольку здесь предполагается, что = с* ширина зоны дается выражением

(Ч*),-^- ^(6Л-³⁸⁾

Если / 1, то эти зоны называются запрещенными зонами высшего порядка, поскольку в соответствии с (6.1.37) и (6.1.34) они имеют место при более высоких частотах. Во многих случаях коэффициент фурье-разложения е, с ростом I уменьшается (т. е. е, -- 0 при / -- оо). Как видно из (6.1.38), соответствующие запрещенные зоны имеют небольшую ширину. На рис. 6.2, б представлены дисперсионные кривые о) (К) для общего случая.

2 Глава 5

Распространение элск i рома§ шпных во.нi в периолнческич средах 4

Глава 6

(6.4.16)

Распространение электромагнитных волн в периодических средах 5

Глава 6

(6.4.16)

Распространение электромагнитных волн в периодических средах 8

Оставить комментарий © Copyright Млекоченко Николай Федорович (vlanko1@mail.ru) Размещен: 10/03/2011, изменен: 10/03/2011. 20k. Статистика. Интервью: Фантастика Иллюстрации/приложения: 6 шт.		Ваша оценка:

Млекоченко Николай Федорович : другие произведения.

Несмотрнте