Тельнин Вячеслав Павлович. Топология числовой прямой

Топология числовой прямой.

Вячеслав Тельнин

Аннотация

Эта статья имеет дело с числовой прямой. Обычно она считается одномерным объектом.

Но если учесть бесконечно большие и бесконечно малые числа, то эта линия окажется более сложным объектом с бесконечным числом самопересечений в неком многомерном пространстве.

Оглавление

1 Большие и маленькие числа 1

2 Пересечения и самопересечения положительной и отрицательной числовых прямых 3

1 Большие и маленькие числа.

Числовая прямая для средних чисел выглядит так:

Рассмотрим большие числа. Вот уравнение для первого большого числа:

X + 1 = X (1)

Обозначим решение уравнения (1) как N1. N1 очень похоже на число натуральных чисел.

И образуем второе большое число - N2- так:

N2 = 2 ^ N1 (2)

N2 > N1 (3)

А N2 очень похоже на число действительных чисел.

Третье большое число построим таким же образом:

N3 = 2 ^ N2 (4)

N3 > N2 (5)

Четвёртое большое число:

N4 = 2 ^ N3 (6)

N4 > N3 (7)

И так далее ...

Рассмотрим маленькие числа. Вот уравнение для первого маленького числа:

x + 1 = 1 (8)

Обозначим решение уравнения (8) как n1. Из (1) следует:

N1 - N1 = 1 (9)

N1*(1 - 1) = 1 (10)

Из (8) следует: n1 = 1 - 1 (11)

(10) + (11) = (12) n1 = 1/N1 (12)

Второе маленькое число n2 образуем так: n2 = 1/N2 (13)

(3) + (12) + (13) = (14) n2 < n1 (14)

And n3 = 1/N3 (15)

n3 < n2 (16)

n4 = 1/N4 (17)

n4 < n3 (18)

И так далее ... .

Итак, у нас есть теперь две числовые прямые:

-- Пересечения и самопересечения положительной и отрицательной числовых прямых.

Определение (11) даёт нам уравнение (19):

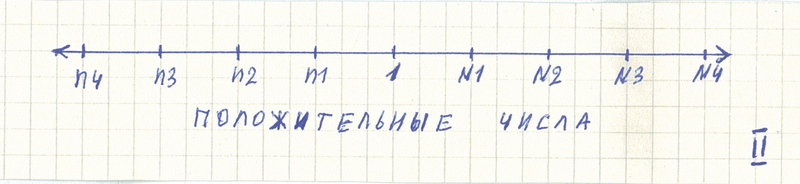
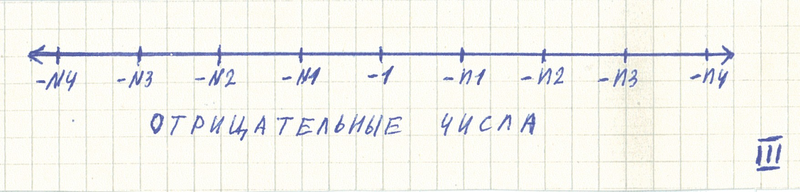
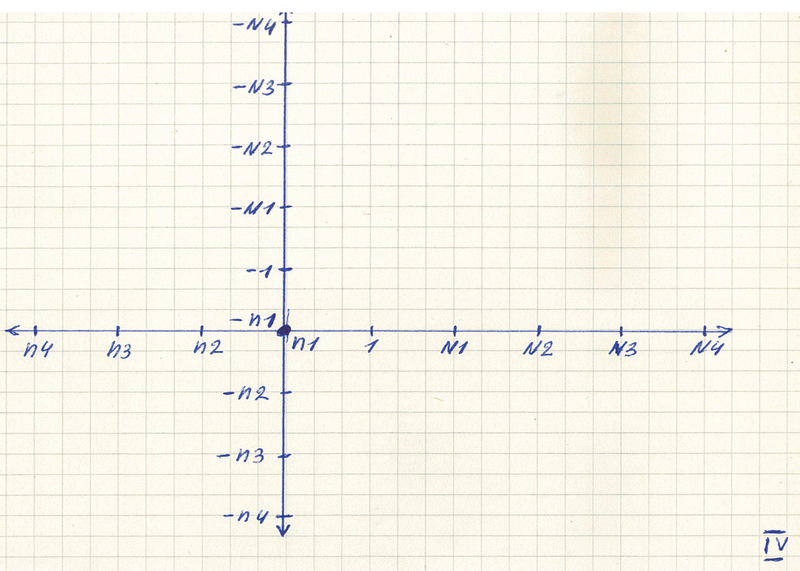
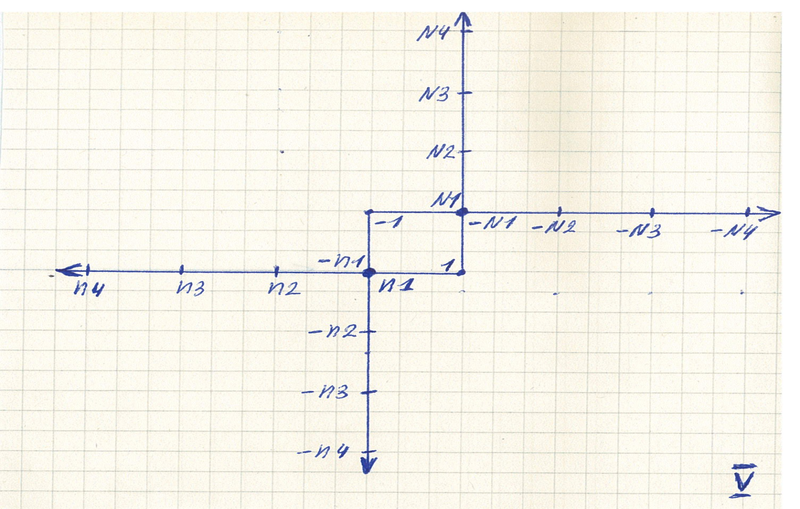
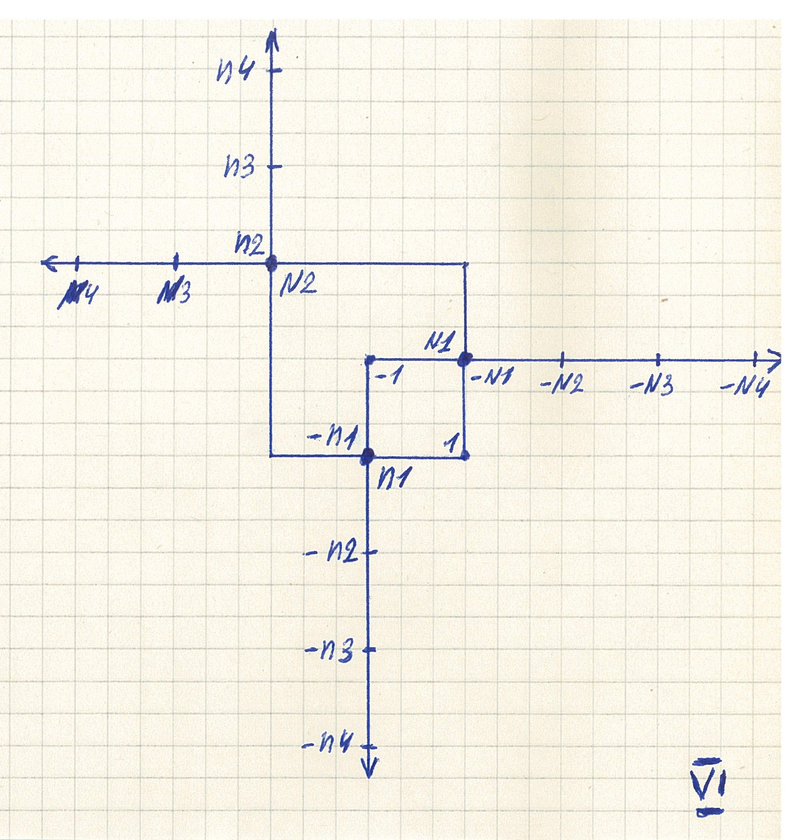
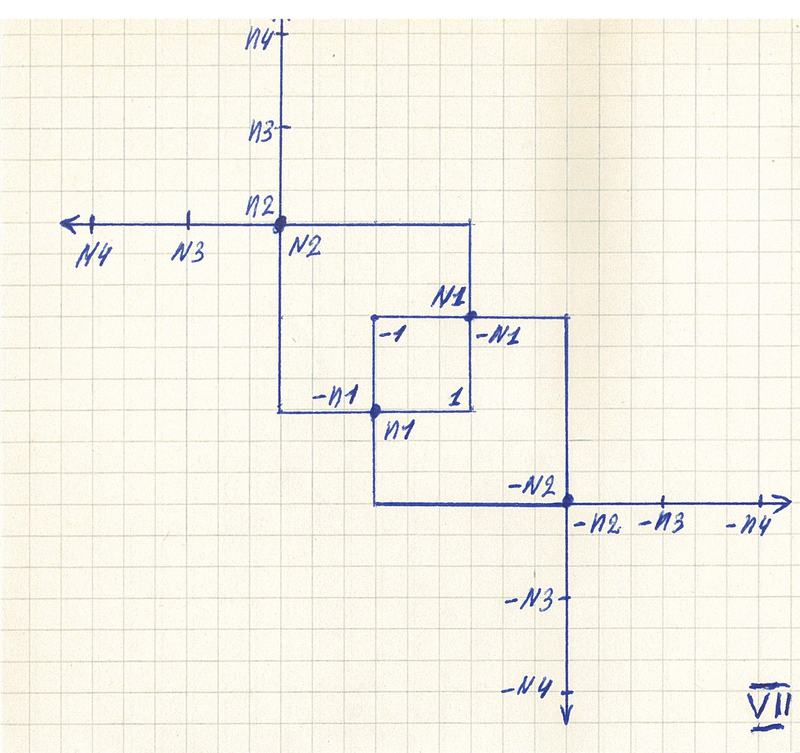
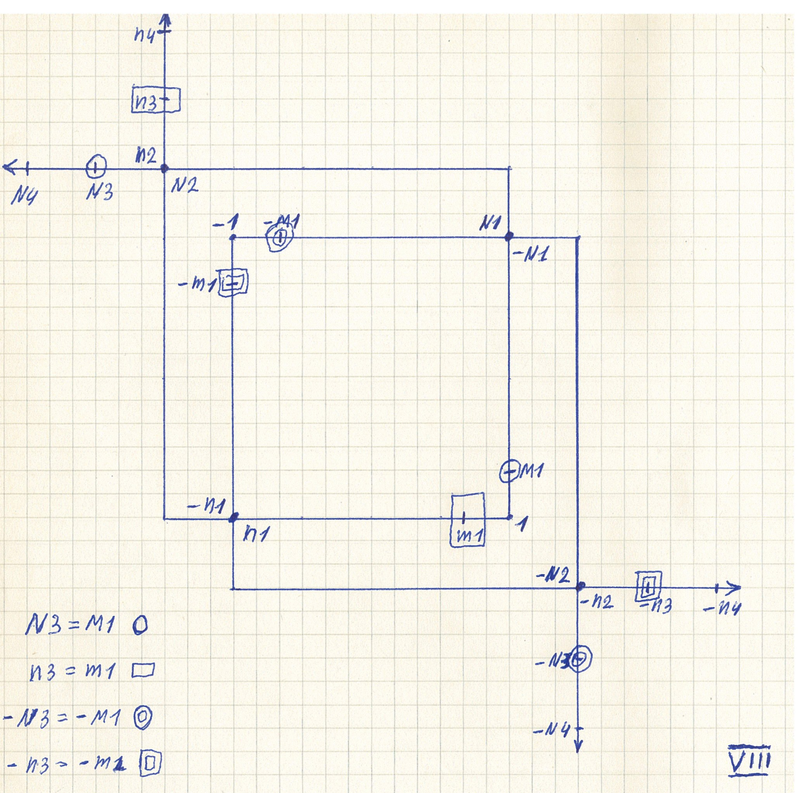
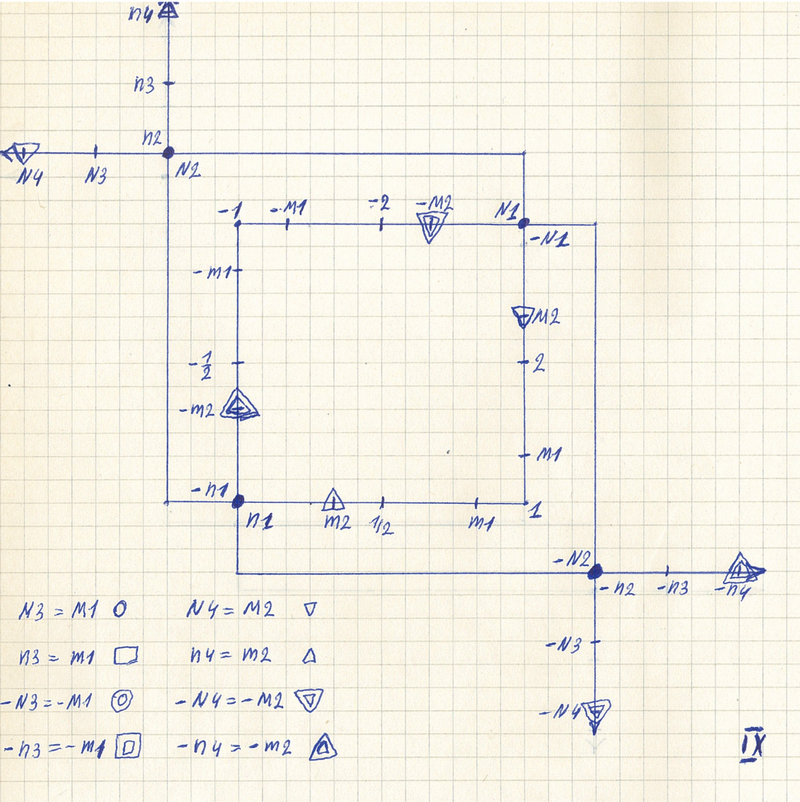
-n1=-(1-1)=-1+1=1-1=n1 ; -n1=n1(19) ; И мы рисуем: 0x01 graphic

Определение (1) даёт нам уравнение (20):

N1 + 1 = N1; -N1 - 1 = -N1; -N1 = -N1+1; -N1 = N1 (20) И мы рисуем:

(2)+(13)+(20): n2 = 1/N2 = 1/(2^N1)=2^(-N1)=2^(N1)=N2 n2 = N2 (21)

Теперь мы можем нарисовать:

Из (21) мы имеем:

n2 = N2

Умножим это уравнение на -1:

-n2 = -N2 (22)

И мы рисуем:

(4)+(21) дают нам: N3 = 2 ^ N2 = e ^ (n2*ln2) = 1 + n2*ln2 + ...

Определим M1 так: M1 = 1 + n2*ln2 + ... (23) Тогда N3 = M1 (24)

(15), (23), (24) дают нам: n3 = 1/N3 = 1-n2*ln2 + ...

Определим m1 так: m1 = 1 - n2*ln2 + ... (25)

Тогда n3 = m1 (26)

И из (24) и (26) мы имеем :

-N3 = -M1 (27)

-n3 = -m1 (28)

Теперь мы можем нарисовать:

Необходимо загнуть стрелку вместе с N4из N3 в 3-е измерение и перенести её через 2 линии а затем спуститься к M1 и пронзить её. И N4 со стрелкой окажутся с другой стороны плоскости рисунка. И N3 совпадёт с M1. Так же будет не только с (N3 и M1), но также и с другими 3-мя парами точек: (n3 и m1), (-N3 и -M1), (-n3 и -m1).

(6), (24), (23) : N4 = 2 ^ N3 = 2 ^ M1 = 2 ^ (1+n2*ln2+...= 2+2*n2*ln2+...

Определим M2 так: M2 = 2^M1 = 2 + 2*n2*ln2 + ... (29)

Тогда N4 = M2 (30)

Из (17), (30), (29) следует :

n4 = 1/N4 = 2^(-M1) = 2^(-1-n2*ln2-...) = 1/2-1/2*n2*ln2+...

Определим m2 так: m2 = 2^(-M1) = 1/2 - 1/2 * n2*ln2 + ... (31)

Тогда n4 = m2 (32)

И из (30), (32) следует: -N4 = -M2 (33) -n4 = -m2 (34)

Теперь мы можем нарисовать: 0x01 graphic

И этот процесс образования новых больших, маленьких, средних чисел и выявления между ними совпадений бесконечен.

Теперь мы видим, что такая простая числовая прямая имеет очень сложную топологическую структуру, которая требует для полного своего проявления применения многомерного векторного пространства.

9/9 - 2013

Оставить комментарий © Copyright Тельнин Вячеслав Павлович (telnin.vyach@gmail.com) Размещен: 11/07/2013, изменен: 09/09/2013. 7k. Статистика. Статья: Естествознание Иллюстрации/приложения: 9 шт.		Ваша оценка:
Аннотация: Введены большие и малые числа на числовой прямой. И одни числа начинают совпадать с другими. Топология числовой прямой становится сложной.

Тельнин Вячеслав Павлович : другие произведения.

Топология числовой прямой