Взаимные переходы состояний Белла
Путенихин П.В.
m55@mail.ru
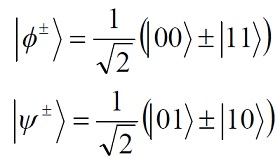
![]()
![]()
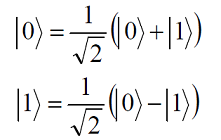
![]()
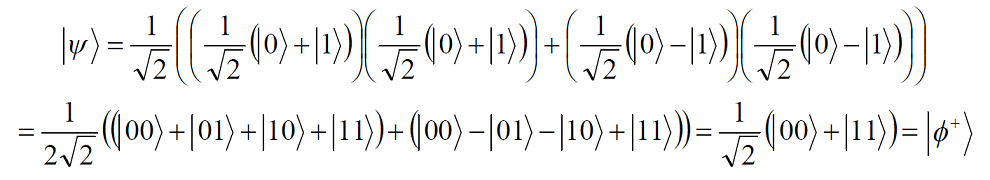
![]()
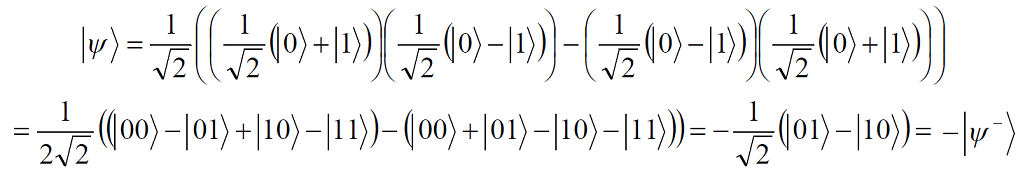
![]()
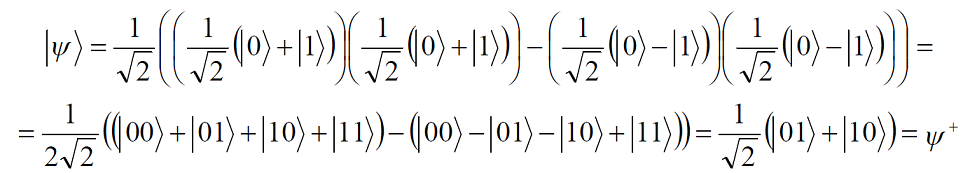
![]()
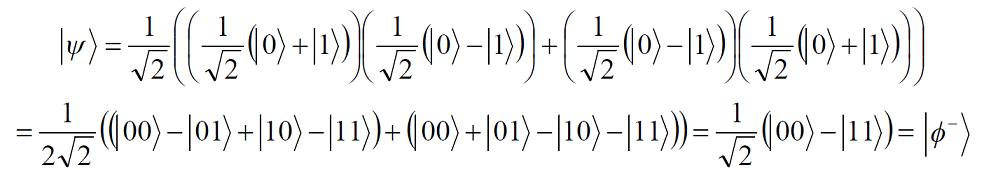
14.10 - 02.11.2013
|
|
||
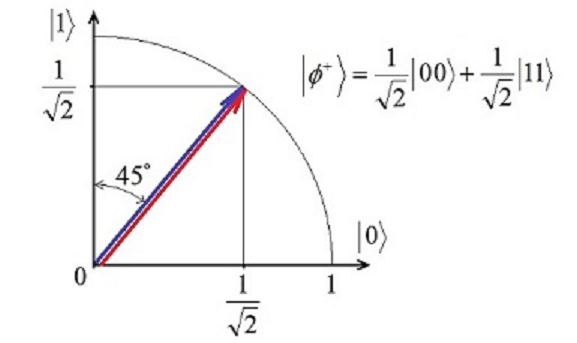
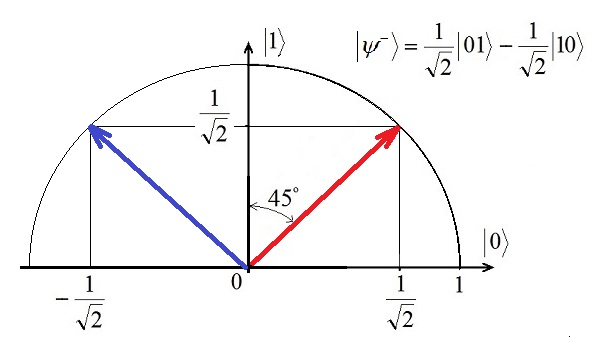
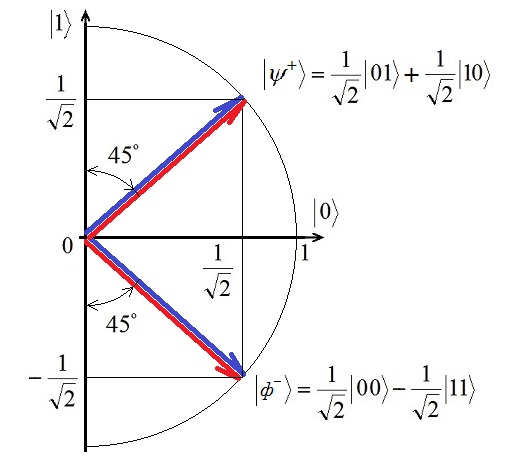
Приведён анализ свойств запутанных частиц (состояний Белла). Показано, что после поворота гейтом Адамара белловских состояний два из них переходят друг в друга | ||
Взаимные переходы состояний Белла
Путенихин П.В.
m55@mail.ru
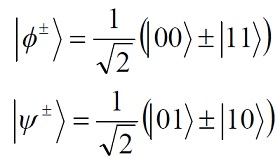
![]()
![]()
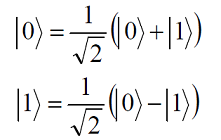
![]()
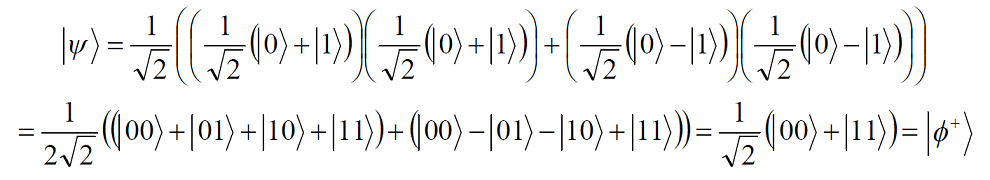

![]()

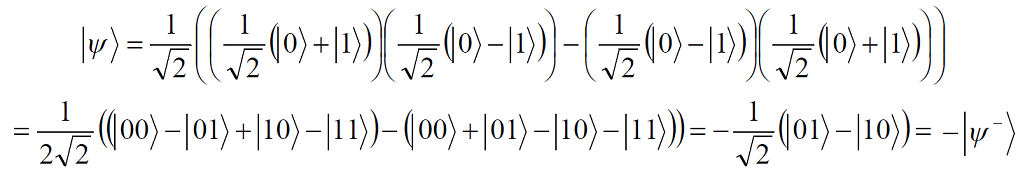
![]()
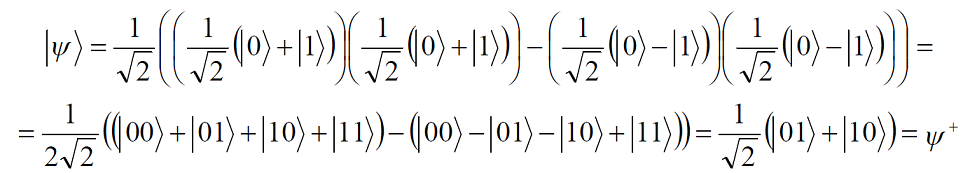

![]()
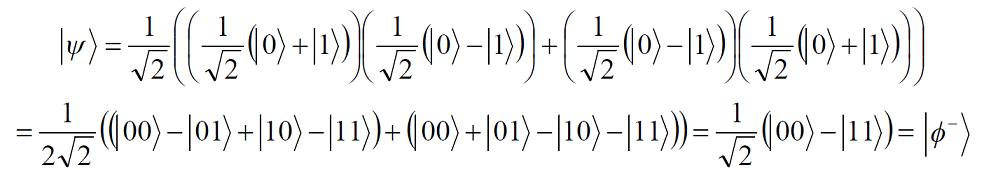
14.10 - 02.11.2013
|