Путенихин Петр Васильевич. Дифференциал площади круга ds

Дифференциал площади круга dS

Оглавление

Аналитическое интегрирование простое

Интегральное уравнение со сложным дифференциалом

Численное интегрирование с точным элементом

Численное интегрирование простое

Аннотация

Представлены исследования различных видов дифференциала dS площади круга, диска и их эквиваленты - элементарные конечные элементы площади. Целью является получение такой формы элементарного участка площади, с которой интегральное уравнение силы притяжения звёзд галактикой для численного компьютерного интегрирования будет иметь наиболее простую форму.

Ключевые слова

интеграл, дифференциал, круг, площадь, галактика, галактическая звезда, сумма элементов, численное интегрирование

Дифференциал площади круга dS

Для вычисления кривой вращения некоторой звёзды на краю галактики нам необходимо вычислить силу притяжения этой звёзды галактикой. Поскольку звезда испытывает гравитационное притяжения от звёзд, разбросанных по всему объёму площади галактики, уравнение явно имеет интегральную форму. Вместе с тем, вычисление интеграла на компьютере сводится к вычислению конечного числа элементов. Интеграл мы заменяем суммой, поскольку никакой даже самым мощный супер компьютер по определению не способен работать с дифференциалами, то есть бесконечно малыми величинам. Вычисление компьютером псевдо-интегральной суммы может быть выполнено только с конечной, то есть, ограниченной точностью. В этой связи нам следует преобразовать точный аналитический интеграл в приблизительную сумму.

Возникает вопрос, как представить дифференциал площади круга dS в виде конечного элемента ΔS, поскольку возможны два подхода: грубый и максимально точный. Первый вариант, грубый даёт заведомо более высокую погрешность, но существенно упрощает уравнение. Целесообразно определить величину погрешности. Очевидно, она будет зависеть от величины элемента ΔS. Чем на большее количество этих малых участков площади мы разобьём диск, круг галактики, тем, очевидно погрешность будет меньше.

Исследование проведём сначала на аналитических дифференциалах dS и интегральных вычислениях.

Аналитическое интегрирование простое

Рассмотрим на диске, круге некоторый элементарный участок площадью dS. Этот элемент dS удалён от центра круга на расстояние x.

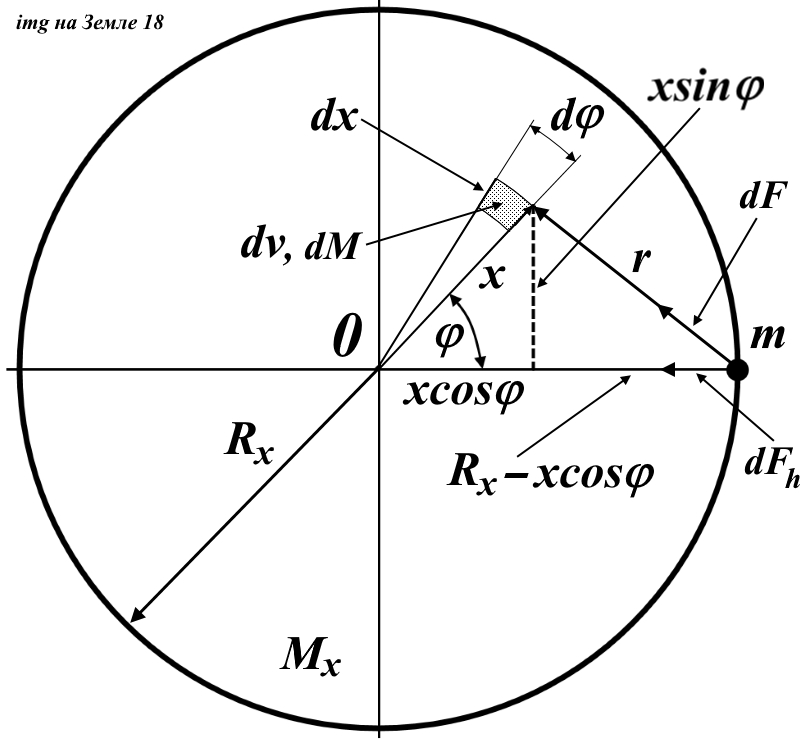
Дифференциал dS

Интегральное вычисление площади круга

Образован он угловым сегментом dφ текущего угла φ и имеет в радиальном направлении дифференциальную толщину dx. Следовательно, площадь элементарного участка равна

Радиус круга, диска галактики равен R. Используя сформированный дифференциал площади dS, найдём интегрирование площадь диска всей галактики

Дифференциал dS

Для наглядности, выделяем квадратными скобками внутренний интеграл. Интегралы простые, последовательно вычисляем их

Дифференциал dS

Видим, что эта простая форма дифференциала даёт правильный результат и, очевидно, никакие его усложнения не нужны. Тем не менее, проверим и более сложный вариант дифференциала.

Интегральное уравнение со сложным дифференциалом

Рассмотрим более точное представление дифференциала площади круга, диска. Будем считать, что это элемент образован двумя кругами, на промежутке между которыми вырезан угловой сегмент. Внешний круг имеет радиус x₁, а внутренний - радиус x₂. Разница площадей, таким образом, образует площадь этого элементарного обруча, для краткости назовём его так. Полная площадь этого обруча равна

(1)

Разбиваем ее на n, которое в дальнейшем устремим к бесконечности, угловых сектора

Дифференциал dS
(2)

Мы здесь сразу же записали эту площадь как дифференциал, хотя в уравнении пока этого не видно. Дело в том, что мы подразумеваем настолько близкие значения радиусов, что они и образуют такую дифференциальную площадь. Каждый сектор, сегмент имеет угловой размер dφ, причём

Дифференциал dS

Мы планируем устремить n к бесконечности, поэтому сразу же записываем элемент угла как дифференциальный. Отсюда

Дифференциал dS

Подставляем в (2)

Дифференциал dS

Запишем полученное уравнение кратко

Дифференциал dS
(3)

Делаем проверку - интегрируем

Дифференциал dS

Получили исходное уравнение (1), следовательно, вычисления верные. Преобразуем уравнение (3)

Дифференциал dS

Толщину обруча, разницу радиусов кругов теперь мы записываем, как и планировали, в виде дифференциала

Дифференциал dS

Можно сказать, что x₂ изменяется от 0 до R - dx, а x₁ - от dx до R. Однако при реальном значении дифференциала dx→0, поэтому каждый из радиусов изменяется от 0 до R. Фактически, в области бесконечно малых величин радиус внешнего круга равен радиусу внутреннего, плюс бесконечно малый дифференциал. Иначе говоря, радиусы равны, а "большая" бесконечно малая величина и "малая" бесконечно малая величина - это одно и то же. Но в уравнении мы учитываем эту бесконечно малую разницу радиусов. Заменяем малый радиус на большой с учётом этой разницы на дифференциал dx

Дифференциал dS

Дифференциал dS
(4)

Для проверки корректности уравнения, интегрируем, ожидая получить в результате площадь всего круга πR². Интегрированием по углу, находим элементарную площадь обруча целиком

Дифференциал dS

Поскольку для переменной, угла φ подынтегральная функция является константой, выносим её за пределы этого интеграла

Дифференциал dS
(5)

Далее интегрируем по х, помня, что, как мы отметили выше, диапазон изменения этой переменной от 0 до R

Дифференциал dS

Замечаем, что интеграл имеет довольно непривычный вид, поскольку в нём присутствуют два тождественных дифференциала dx. Разбиваем интеграл на два

Дифференциал dS

Дифференциал dS
(6)

Правый, необычный интеграл следует вычислять с большой осторожностью. Исследуем его

Дифференциал dS

Интегрируемой величиной является dx без скобок, а подынтегральной функцией - (dx), величина в скобках. Мы интегрируем функцию (dx), о которой мы можем с уверенностью заявить: в процессе интегрирования величина этой функции всегда неизменна, но равна дифференциальному нулю (dx)=0. Изменяется только дифференциал dx. Следовательно, этот интеграл равен нулю по определению. Запишем это явно

Дифференциал dS

С учетом этого интегрируем оставшийся интеграл (6)

Дифференциал dS

Запишем кратко

Это полная площадь круга, что и требовалось найти. Таким образом, при вычислении силы притяжения массивного дискообразного тела мы вполне можем использовать площадь элементарного элемента диска (4)

Дифференциал dS
(7)

Вместе с тем, видим, что это заметно более сложная запись дифференциала, которая, несомненно, приведёт и к более сложной записи интеграла для вычисления сил притяжения. Поэтому разумнее отказаться от этой записи и использовать более простую.

Численное интегрирование с точным элементом

На самом деле, интегрирования как такового нет, есть суммирование элементарных участков диска, имеющих малую площадь. Рассмотрим такой элементарный участок площадью ΔS в варианте для компьютерных вычислений. Пусть эти участки образуют на диске элементарный обруч. Собственно обруч образован промежутком между двумя окружностями радиуса x₁ и x₂. Следовательно, полная точная площадь этого элементарного обруча равна

Разбиваем этот обруч на n угловых участков. Площадь этого малого углового элемента обруча будет равна

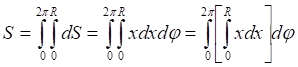
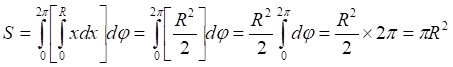
Дифференциал dS

Преобразуем

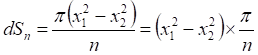
Дифференциал dS

В левых скобках видим толщину обруча, которую обозначим ка элементарный интервал по радиусу Δх, эквивалент дифференциала, запишем это

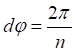
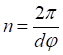
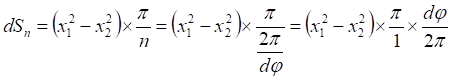
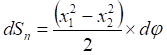
Дифференциал dS

Используем для вычислений в качестве текущей переменной диаметр большего круга, x₁

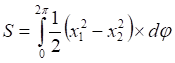
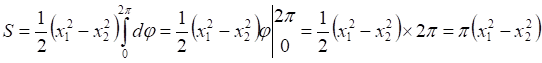
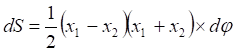
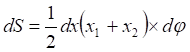
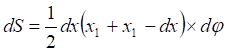
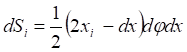
Дифференциал dS

Поскольку обруч разбит на n угловых участков, величина этого элементарного угла равна

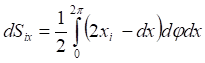
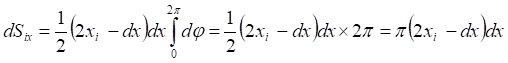
Дифференциал dS

Отсюда

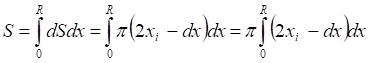
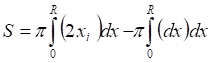
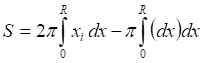
Дифференциал dS

Следовательно

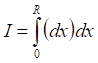
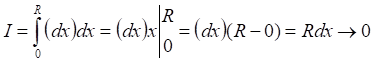
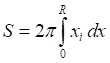
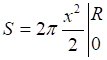
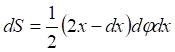
Дифференциал dS

В краткой записи

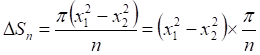
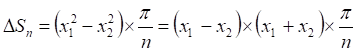
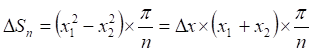
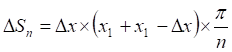
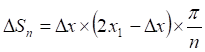
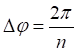
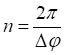
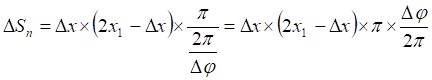
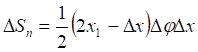
Дифференциал dS
(8)

Подсчитаем сумму всех элементарных участков всех обручей, рассчитывая получить полную площадь диска. На первом этапе получим площадь целого частного обруча. При фиксированном значении его радиуса эта величина будет получена простым умножением на число угловых сегментов обруча

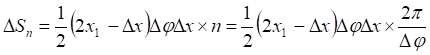
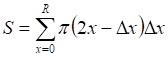
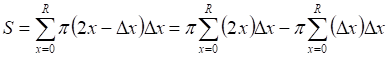
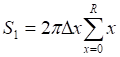
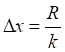
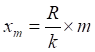
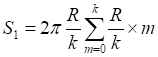
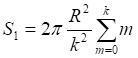
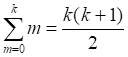
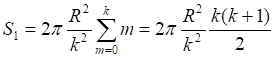
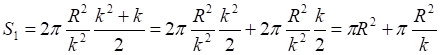
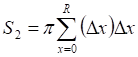
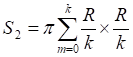
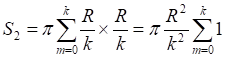
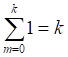
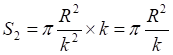
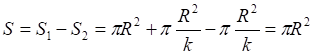
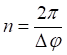
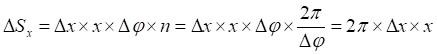
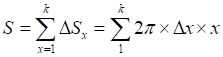
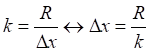
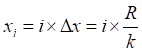
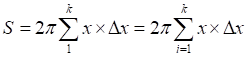
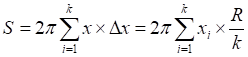
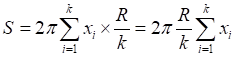
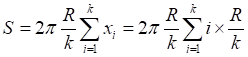
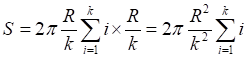
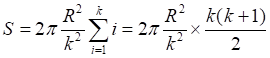
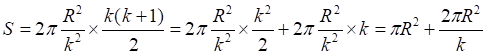
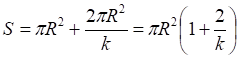
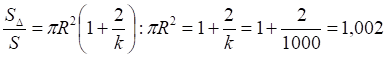
Дифференциал dS

Теперь, чтобы найти полную площадь диска, необходимо просуммировать площади всех элементарных обручей

Дифференциал dS

Разделим сумму на две суммы

Дифференциал dS

Рассмотрим первое слагаемое

Дифференциал dS

Величина Δx имеет конечное значение, определяемое разбиением R на отрезки

Дифференциал dS

Соответственно, каждое значение x также определяется через этот коэффициент разбиения

Дифференциал dS

Внесем эти определения в уравнение для S₁

Дифференциал dS

Знак суммы здесь теперь означает "сумма всех порядковых числительных от 0 до k". Эта сумма определяется известным уравнением

Дифференциал dS

Поэтому получаем значение первой суммы S₁

Дифференциал dS

Раскрываем скобки

Дифференциал dS

Замечаем, что получена площадь всего диска плюс какая-то добавка. Но у нас есть второе слагаемое, отрицательная сумма S₂. Возможно, она уничтожит эту добавку. Рассмотрим это второе слагаемое

Дифференциал dS

Как и выше заменяем переменные на их известные значения

Дифференциал dS

Обращаем внимание, что под знаком суммы находятся константы, не зависящие от переменной суммирования. Выносим их за знак суммы

Дифференциал dS

После выноса констант под знаком суммы осталась очевидная единица. Смысл этой суммы достаточно прост: просуммировать k-раз эту величину, поэтому

Дифференциал dS

Следовательно

Дифференциал dS

Помним, что эта сумма - отрицательная, поэтому

Дифференциал dS

Это полная площадь круга, что и требовалось найти. Следовательно, при компьютерном, дискретном вычислении силы притяжения массивного дискообразного тела мы вполне можем использовать точную дискретную площадь элементарного элемента диска (8). Обращаем внимание, что это уравнение в точности повторяем дифференциальное уравнение (7), что, в общем-то, не удивительно.

Численное интегрирование простое

Итак, мы пришли к выводу, что и сложная и простая форма записи дифференциала dS дают в конечном счёте один и тот же результат, то целесообразно такую же проверку сделать и для конечной величины дифференциала - конечного элемента ΔS, которую предполагаем использовать в компьютерных вычислениях.

Рассмотрим площадь элементарного участка ΔS в качестве варианта дифференциала dS. Полная площадь элементарного обруча диска

Площадь этого элементарного обруча радиусом x и толщиной Δx в данном случае равна сумме n этих элементов, где n - число элементов, на которое разбит этот обруч

Очевидно, что

Дифференциал dS

Следовательно

Дифференциал dS

Получается буквально, что точность вычислений не зависит от числа элементов разбиения обручей! Это довольно странно. Рассмотрим, чему равна сумма площадей всех обручей, будет ли она равна известной площади круга

Дифференциал dS

Здесь уже k - это количество обручей, величина, на которую разбит радиус круга. Очевидно

Дифференциал dS

Соответственно

Дифференциал dS

Переписываем уравнение суммы

Дифференциал dS

Поскольку величины k и R определены заранее, то также оказывается определённым заранее и значение Δx. Подставляем эти известные величины в уравнение суммы

Дифференциал dS

Величина дроби является константой, поскольку состоит из констант, заданных заранее и этот сомножитель содержится в каждом слагаемом суммы. Следовательно, его можно вынести за знак суммы

Дифференциал dS

Известна также и величина радиуса каждого обруча x_i

Дифференциал dS

Вновь видим константу, общий множитель каждого слагаемого суммы. Выносим и его за знак суммы

Дифференциал dS

Под знаком суммы остался порядковый номер слагаемых. То есть, сумма явлется суммой k порядковых чисел. Уравнение для вычисления этой суммы известно

Дифференциал dS

Раскрываем скобки

Дифференциал dS

Получается, что площадь зависит от дискретности разбиения

Дифференциал dS

Площадь, вычисленная с использование конечного размера "дифференциала" текущего радиуса Δx, тем сильнее превышает реальную площадь круга, чем меньше число интервалов k. В частности, используемое в наших вычислениях k=1000, даёт ошибку площади

Дифференциал dS

то есть, менее 0,2%. Следует признать такое отклонение хорошим. И вновь вывод: усложения при формировании конечного значения ΔS по новому способу излишни. При формировании интеграла для компьютерного вычисления силы притяжения звёзд дисковой галактикой целесообразно использовать это короткое уравнение

08.02.2021

Оставить комментарий © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru) Размещен: 08/02/2021, изменен: 08/02/2021. 21k. Статистика. Статья: Естествознание Темная космология Иллюстрации/приложения: 73 шт. Скачать FB2		Ваша оценка:
Аннотация: Представлены исследования различных видов дифференциала dS площади круга, диска и их эквиваленты - элементарные конечные элементы площади. Целью является получение такой формы элементарного участка площади, с которой интегральное уравнение силы притяжения звёзд галактикой для численного компьютерного интегрирования будет иметь наиболее простую форму.

Путенихин Петр Васильевич : другие произведения.

Дифференциал площади круга ds