Опря В. Р.
Теория относительности, как топология времени
1. Парадоксы теории относительности
1.1 О чем эта статья

1.2 Миф о замедлении времени
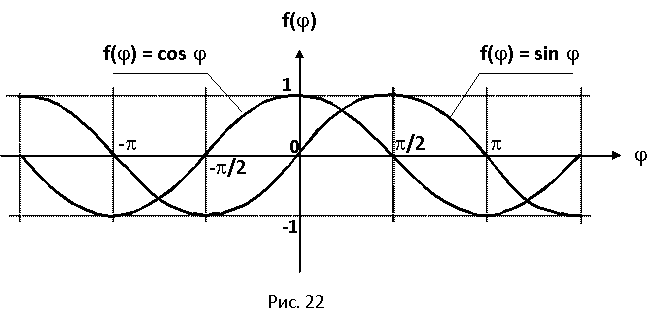
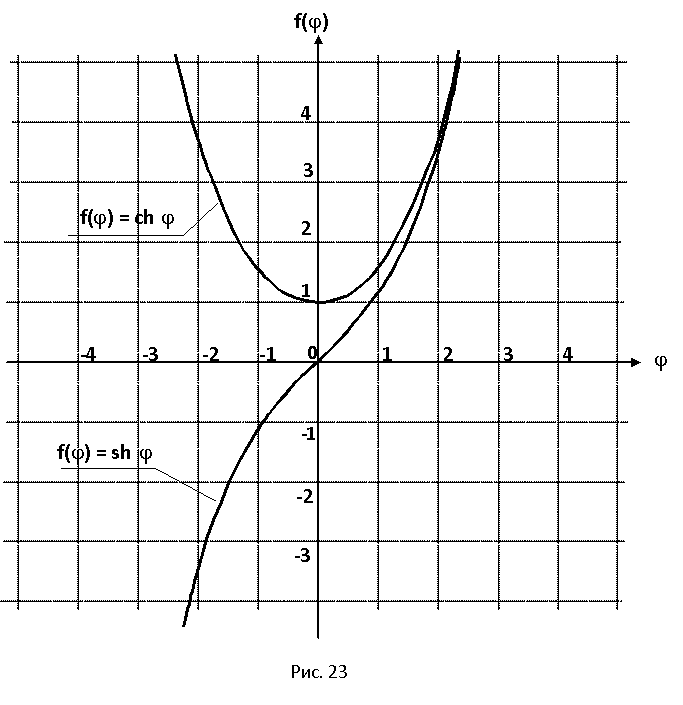
1.3 Эффект лазерной указки и одновременность
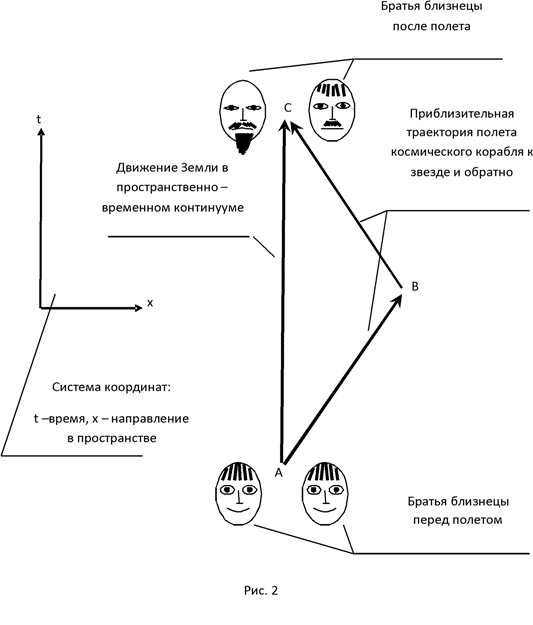
1.4 Большое путешествие
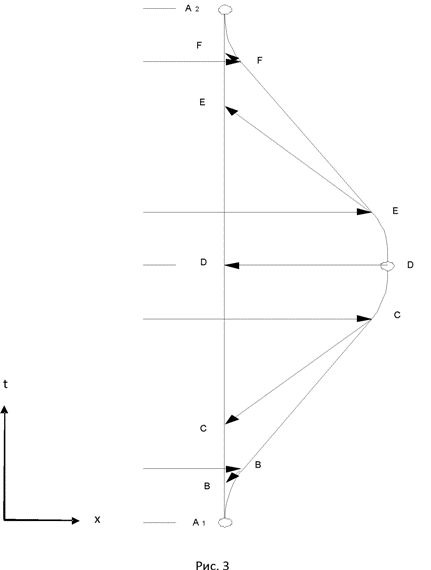
1.5 Путешествие наоборот
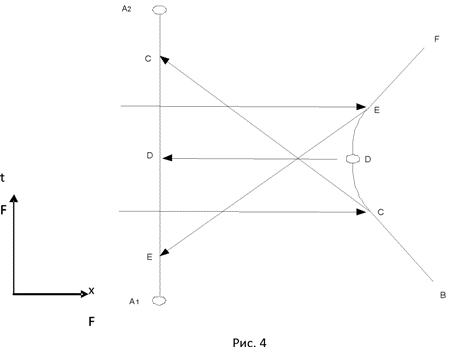
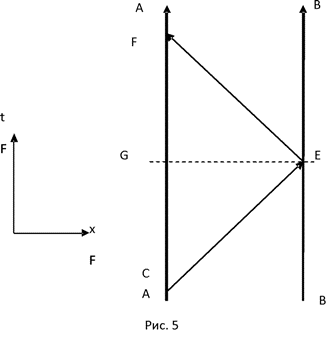
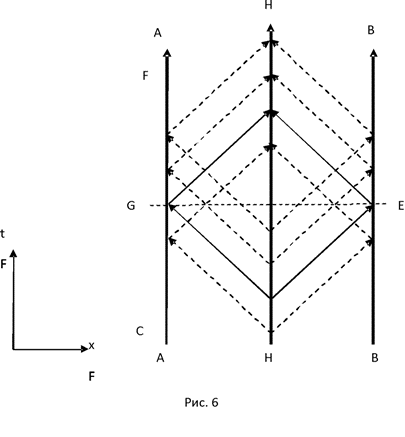
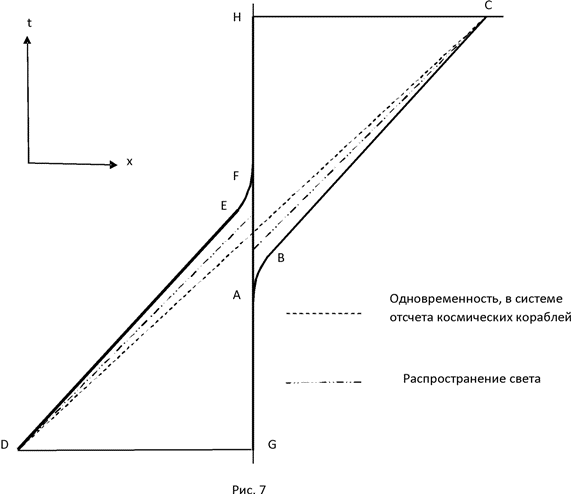
2. Пространство и время
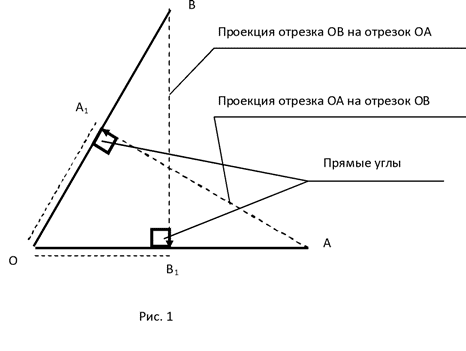
2.1 Геометрия Минковского
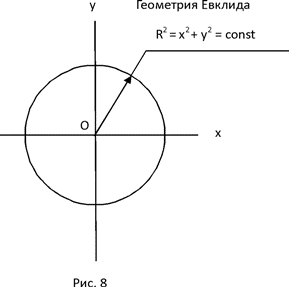
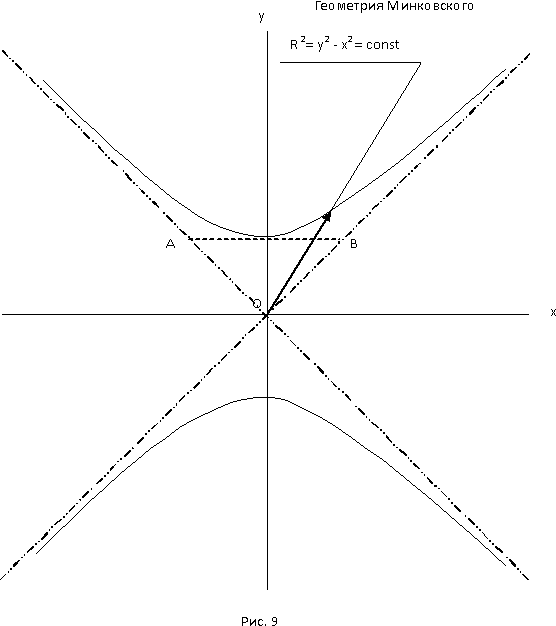
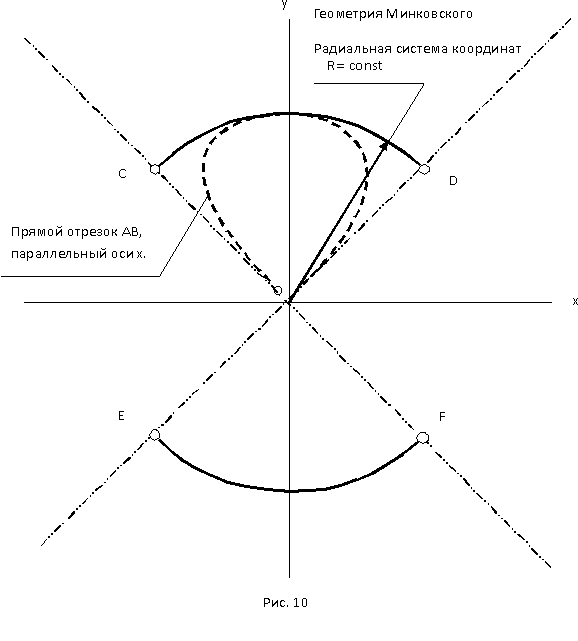
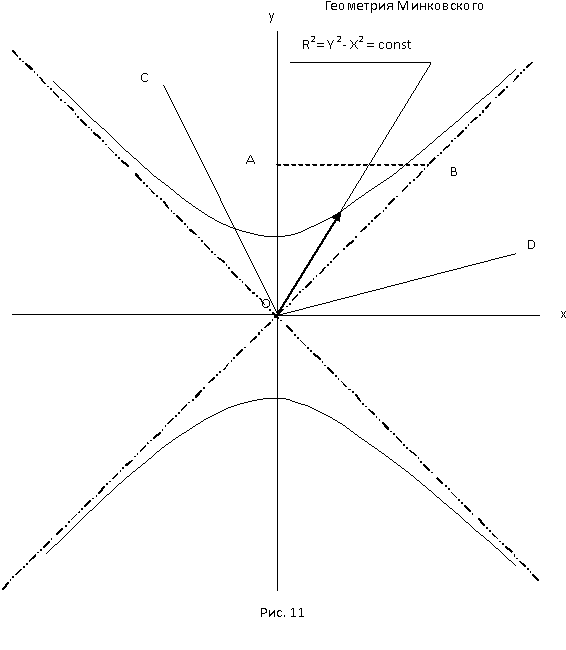
2.2 Системы координат и системы отсчета
2.3 Интервал

2.4 Причина и следствие
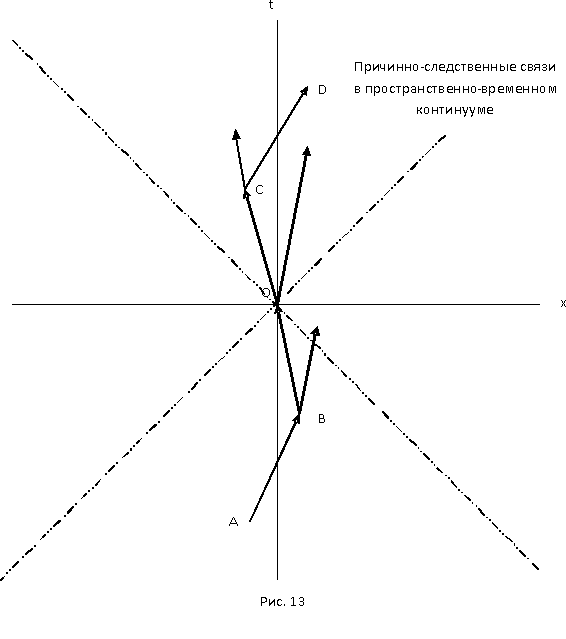
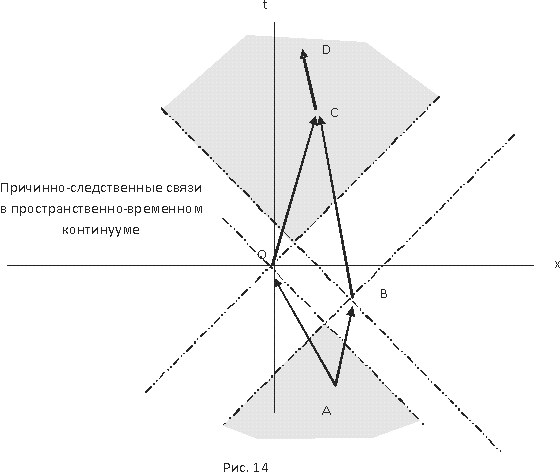
2.5 Мнимое и действительное
2.6 Топология времени
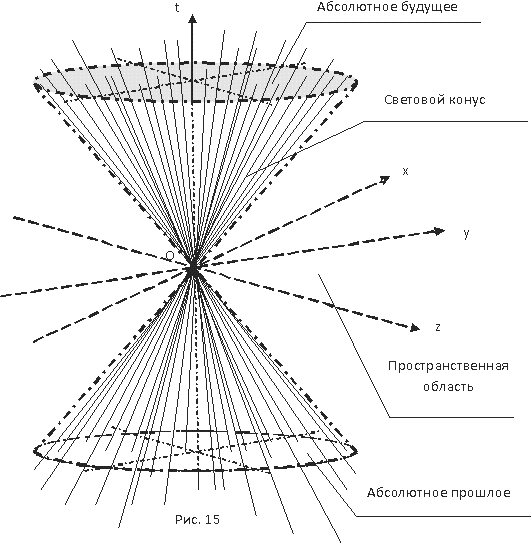
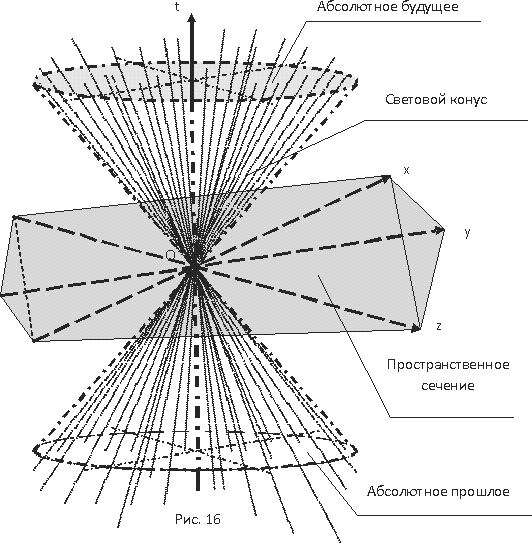
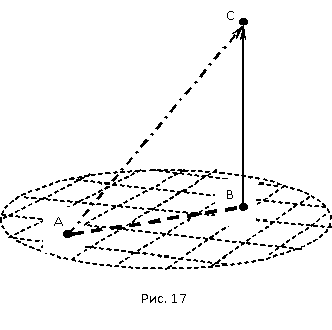
3. Основы топологии времени
3.1 Аналог сферы в топологии времени

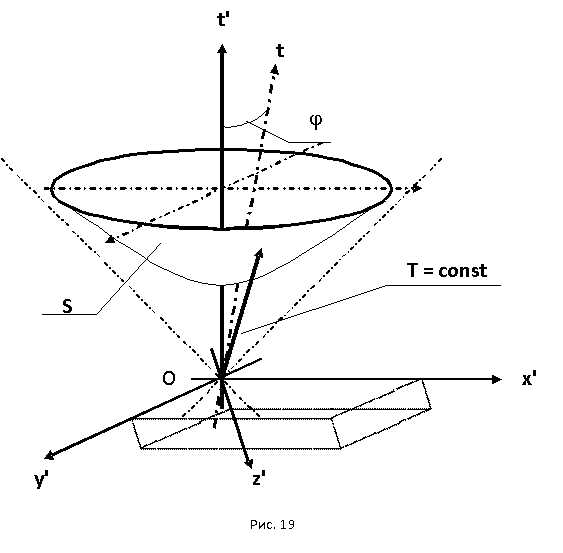
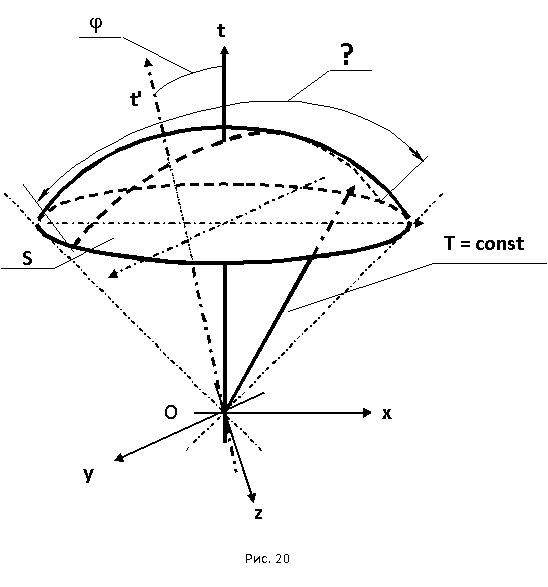
3.2 Гиперболическая тригонометрия