Опря В. Р.
Часть четвертая
Парадокс близнецов. Все за и против
Содержание
Предисловие
1. "Большое путешествие" в теории эфира Лоренца
2. Формулировки парадокса близнецов
3. Приближенный расчет большого космического путешествия
4. Абсолюты теории относительности
5. Полет до середины пути
6. Поворот системы отсчета
7. Ускоренное движение
8. Эксперимент со свободно падающими часами
9. Полет по "змейке"
10. Релятивистский эффект Доплера
11. Предварительные итоги
Цитируемая литература
Предисловие
Казалось бы, парадокс близнецов полностью опровергается всего несколькими фразами Альберта Эйнштейна. Цитирую:
"Теория утверждает равноценность только всех галилеевых (неускоренных) систем координат, т. е. таких систем координат, по отношению к которым в достаточной мере изолированные материальные точки движутся прямолинейно и равномерно. такой системой координат является, конечно, система K, но не ускоряемая время от времени система K'. Поэтому нельзя выдвинуть никаких возражений против основ теории относительности, исходя из того результата, что часы U2 после передвижения туда и обратно отстают от часов U1".
Но, все дело в том, что простой мысленный эксперимент со свободно падающими часами в кабине ускоренно движущегося космического корабля показывает, что время в нем идет точно так же, как и в инерциальной системе отсчета, в данный момент времени неподвижной относительно космического корабля. Одного этого достаточно, чтобы опровергнуть предложенное Эйнштейном объяснение. И можно поставить множество других экспериментов, которые тоже свидетельствуют, что объяснение, предложенное Эйнштейном, неверно.
В 1905 - 1918 годах теория относительности не была закончена. Эйнштейн это знал лучше других, поэтому продолжал попытки построить окончательную теорию до самой смерти. В двадцатых годах разрабатывал теорию релятивистского эфира, затем занимался идеей увеличения числа измерений, но окончательная теория так и не была создана. Теория относительности в том виде, в котором мы ее знаем по учебникам, вовсе не окончательный вариант. И общая теория относительности (ОТО) вовсе не так непротиворечива и безошибочна, как об этом обычно пишут в учебниках.
Многие годы лучшие силы теоретической физики были направлены на доказательство безошибочности и непротиворечивости теории относительности. Все факты и эксперименты, ставящие под сомнение даже частные концепции теории относительности, объявлялись ненаучными. И, в результате, мы имеем то, что имеем. Допущенные при развитии этой теории ошибки на виду, но никто не обращает на них внимания, потому что сложилась устойчивая иллюзия того, что данная часть теории уж точно безошибочна.
Эта работа не направлена против теории относительности. Она направлена против штампов и предрассудков, против неспособности свободно мыслить. В данной работе я постарался детально описать все известные мне действительно стоящие возражения против объяснения, предложенного Альбертом Эйнштейном. Но, если существует физическое явление, то должно существовать и его объяснение, и логика происходящего достаточно проста, чтобы рассмотреть все возможные варианты. Их не так уж много.
В шахматах есть такое понятие "детский мат". Если вы не знаете, что это такое, то это мат в четыре хода черному королю, который возможен только в том случае, когда человек, играющий за черных, умеет только переставлять фигуры, но не видит ни угроз, ни способов их отражения. Подобная партия может выглядеть так:
1) e2-e4 a7-a6 2) Сf1-c4 a6-a5 3) Фd1-f3 h7-h5 4) Cc4-f7 мат.
Все доказательства парадокса близнецов, которые мне попадались, в том числе и доказательство, которое опубликовал в 1918 году Альберт Эйнштейн, напоминают мне именно "детский мат". Ситуацию, когда серьезные доводы "против" всерьез не рассматриваются. Я же, предлагаю сыграть "за обе стороны", и за "черных", и "за белых", объективно рассматривая и доводы за, и доводы против. И рассмотреть вопрос настолько глубоко, насколько позволяют размеры этой статьи.
Принципиальное отличие этой статьи от большинства критических статей о теории относительности состоит в том, что их авторы выступают против принципов относительности предложенных Эйнштейном в 1905 году. Лично я убежден, что в 1905 году теория относительности начала двигаться в правильном направлении и лишь потом в ней был допущен ряд принципиальных ошибок. И я надеюсь убедить в этом вас.1. "Большое путешествие" в теории эфира Лоренца
Часто, в литературе по теории относительности пишут, что никакого парадокса близнецов нет. Это не совсем верно. Парадокс был сформулирован, следовательно, по крайней мере, в этом смысле, он существует. А вот то, правильно ли он сформулирован, и имеет ли он рациональное объяснение, это совсем другое дело. В формулировке парадокса близнецов действительно есть неверная информация, но, чтобы обнаружить это, нужно было вначале сформулировать парадокс и найти ему какое-то объяснение. Или, даже, несколько альтернативных объяснений. А лишь затем, проанализировав формулировку, ее следствия и объяснения, можно делать выводы.
Объяснение парадокса близнецов, которое принято большинством современных физиков, основано на статье Эйнштейна, опубликованной в 1918 году "Диалог по поводу возражений против теории относительности", в которой он объясняет разницу во времени, прошедшему у близнецов, физическими эффектами, связанными с гравитационным потенциалом. Согласно этому объяснению, в действительности, в теории относительности парадокс не возникает, то есть, видимому парадоксу дается рациональное объяснение, а сомневающиеся в этом объяснении, просто не понимают основных принципов теории относительности.
В утверждении о том, что сомневающиеся в теории относительности, просто не понимают ее основные принципы, есть доля правды. Действительно, в целом ряде попыток опровержения теории относительности Эйнштейна, в которых, в качестве основного аргумента использовался парадокс близнецов, авторы явно не вполне корректно использовали основные принципы теории относительности. Но, вместе с тем, тщательно проработав аргументацию противников и защитников предложенного Эйнштейном объяснения парадокса близнецов, я обнаружил, что аргументация защитников теории относительности от парадокса близнецов тоже не всегда корректна. И не всегда сторонники теории относительности действительно достаточно хорошо понимают ее основные принципы и следствия этих принципов.
Обвинение в непонимании основных принципов теории относительности и ее следствий универсально. Оно может использоваться как сторонниками теории относительности, так и ее противниками. Поэтому, для того, чтобы достаточно компетентно рассуждать о теории относительности, ее основных принципах, следствиях и трудностях, совершенно необходимо более глубокое погружение в тему, чем это делает большинство критиков и защитников. И с этой точки зрения, парадокс близнецов великолепный инструмент для исследования теории относительности.
Иногда парадокс близнецов подается как любопытное явление, связанное с замедлением времени. Два брата близнеца расстаются на космодроме, один из них остается на Земле, а другой отправляется в большое космическое путешествие. Брат путешественник быстро набирает скорость, и затем летит на звездолете с постоянной скоростью, сравнимой со скоростью света, к звезде расположенной за десяток световых лет от Земли, а затем, точно так же возвращается обратно. На Земле братья близнецы встречаются, и их ожидает сюрприз. Оказывается, что один из них, который летал в космос, постарел лет на двадцать, а другой, который оставался на Земле, ... ну скажем, лет на тридцать.
Парадокс? Нет не парадокс, а только любопытное физическое явление. В теории эфира Гендрика Лоренца это интересное физическое явление тоже присутствовало, но там оно не создавало парадокса. В теории Лоренца, точно так же, как в теории относительности, после большого космического путешествия брат домосед будет старше брата путешественника. Точно так же, брат домосед, наблюдая за путешественником, будет считать, что время у того идет медленнее, чем у него. А брат путешественник, двигаясь равномерно и прямолинейно, и используя для измерений метод радарной одновременности, будет считать, что медленнее идет время на Земле. Разница только в том, что у Лоренца эта методика называлась методом k-коэффициентов, а современное название она получила позже.
В теории Лоренца, наша Вселенная это большая физическая иллюзия, в которой обнаружить абсолютную физическую систему отсчета невозможно, она скрыта, но, тем не менее, она существует. Эфир теории Лоренца, это, по сути, само трехмерное физическое пространство, такое, каким мы привыкли оперировать в школе, изучая математику, геометрию и классическую физику. Но, дополнительно, это пространство рассматривается как среда, которая передает электромагнитное излучение и гравитационное взаимодействие. И, когда в теории Лоренца заходит речь об обнаружении абсолютного пространства, имеется в виду обнаружение трехмерного пространственного континуума как физического объекта. А противостоящие Лоренцу физики релятивисты конца девятнадцатого века, во главе с Эрнстом Махом, настаивали на том, что пространство, само по себе, это не физический объект, а просто пустота, вмещающая в себя физические объекты, и никакого взаимодействия между физическими объектами и пространством не существует.
В теории Лоренца, время близнеца путешественника в действительности идет медленнее, чем у брата, оставшегося на Земле, просто потому, что он быстрее движется относительно трехмерного физического пространства - эфира Лоренца. Лоренц это явление объясняет взаимодействием, вероятно, имеющим электромагнитную природу, которое возникает между эфиром и движущейся частицей. По предположению Лоренца, между эфиром и движущейся частицей возникает индукция, которая увеличивает инертную массу частицы, вследствие чего, она становится "менее поворотливой", медленнее реагирует на приложенную к ней силу. И физически это проявляется как увеличение ее инертной массы.
В теории эфира Лоренца инертная масса движущегося тела определяется по формуле
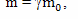
где: m0 - инертная масса, которой обладал этот же объект, если бы он покоился относительно физического трехмерного пространства. И, раз инертная масса у движущегося объекта и всех его составляющих возросла, то для изменения скорости этого объекта на небольшую величину Δv, при одинаковой силе требуется большее время. И, соответственно, если вместе с этим объектом движутся часы, не имеет значения какие, их ход будет замедленным, потому что их части (маятник или электроны) стали массивнее и все физические процессы в них идут медленнее.
Предложенная Лоренцем формула относительного замедления времени движущегося объекта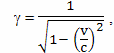
которая обычно в учебниках приводится как формула теории относительности, на самом деле изначально предназначалась для описания воздействия эфира на движущуюся частицу.
Неподвижный относительно трехмерного пространства наблюдатель, все происходящее может интерпретировать как замедление хода времени движущегося объекта в γ раз. Но, в силу принципа физической иллюзии, наблюдатель, движущийся относительно трехмерного пространства, вместе с рассматриваемым объектом и часами, этого замедления не заметит и будет считать, что время замедлялось как раз у неподвижного относительно трехмерного пространства наблюдателя.
Согласно теории эфира Лоренца, нет ничего удивительного в том, что после окончания путешествия близнецы обнаружат разницу в возрасте. В этом случае, необычной является только физическая иллюзия, благодаря которой, движущийся брат близнец не замечает того, что время у него идет медленнее и считает именно себя, а не своего неподвижного относительно физического пространства (эфира) брата домоседа, выделенной системой отсчета. И в теории Лоренца эта иллюзия разрушается, когда брат путешественник уменьшает свою скорость, чтобы сравнять ее с целью путешествия, а затем разгоняется обратно. В это время он обнаруживает, что, по результатам его измерений, время на Земле пошло значительно быстрее, и за месяцы ускоренного движения космического корабля, на Земле проходят годы. Но, в теории Лоренца, это явление объясняется не действием ускорения на ход времени, а тем, что пока действовала иллюзия, на Земле действительно прошли годы. И, чем дольше действовала иллюзия, чем сильнее удалился брат путешественник от Земли, тем большая разница во времени накапливается, и тем интенсивнее проявляется эффект разрушения иллюзии.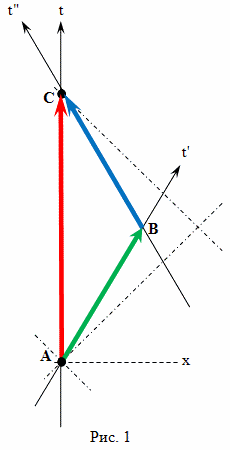
Рассмотрим полет близнеца путешественника с точки зрения теории эфира Лоренца (рис. 1). Предположим, что изначально оба брата близнеца находятся на Земле и их скорость относительно эфира настолько мала, что ей в расчетах можно пренебречь. Один из братьев остается на Земле, и его мировая линия на рисунке обозначена прямой линией AC. Другой брат на ракете быстро разгоняется и движется в сторону выбранной цели с постоянной скоростью. Быстро, это означает, что временем разгона в данном расчете тоже можно пренебречь, поскольку оно существенно меньше общего времени путешествия. Достигнув выбранной цели, в событии B, брат путешественник быстро выравнивает скорость своей ракеты по отношению к эфиру, а затем, быстро разгоняется в направлении Земли и тоже движется с постоянной скоростью. Достигнув Земли, путешественник также, быстро выравнивает свою скорость с Землей (и с эфиром), и сравнивает показания своих часов с часами брата, оставшегося на Земле.
Для наглядности, продемонстрируем происходящее расчетом. Предположим, что цель путешествия располагается на расстоянии L = 1017 метров от Земли. Предположим, что путешественник двигался в направлении своей цели и обратно с одинаковой скоростью 2/3·c, где: c = 299792458 м/с - скорость света в вакууме.
Тогда, путешествие в одну сторону, с точки зрения наблюдателя на Земле, будет продолжаться в течение: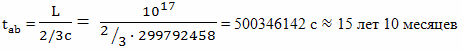
А у движущегося относительно эфира брата путешественника все процессы будут идти объективно замедленно в γ раз, следовательно, по его часам пройдет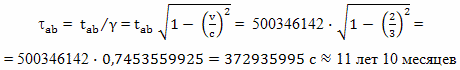
Обратный путь, как мы условились, будет происходить с той же скоростью и займет такое же время. Следовательно, за время путешествия на Земле пройдет почти 32 года, а на космическом корабле всего 26 лет. Если бы путешествие совершалось со скоростью большей чем 2/3 скорости света, или к более далекому объекту, то отличие в ходе часов было бы больше.
А в случае, если Земля вместе с наблюдателем движется, относительно эфира, в теории Лоренца начинает действовать физическая иллюзия. Немного изменим предыдущую задачу. Пусть теперь Земля и цель путешествия не покоятся относительно эфира, а движутся относительно него со скоростью 1/3 скорости света. Пусть расстояние между Землей и целью путешествия по-прежнему будет равно L0 = 1017 метров, с точки зрения наблюдателя с Земли. И пусть, скорость движения путешественника с точки зрения наблюдателя с Земли будет равна 2/3 скорости света.
Для расчета такого путешествия, в соответствии с теорией эфира Лоренца, необходимо учесть сразу несколько физических явлений. Одно из этих явлений состоит в том, что все размеры тел в направлении их движения сокращаются. Земля и звезда, которая является целью путешествия, движутся с одинаковой скоростью и в одном направлении относительно эфира, а, следовательно, расстояние между ними все время остается постоянным, но с точки зрения наблюдателя неподвижного относительно эфира, это расстояние составит: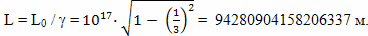
Примерно на 6% меньше, чем с точки зрения наблюдателя с Земли.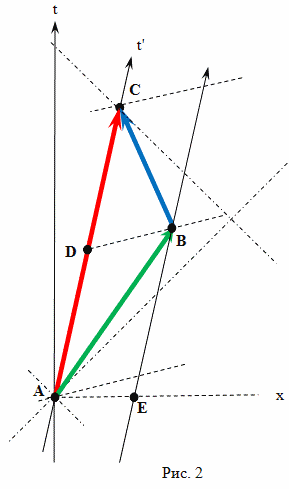
Мировая линия Земли AC в данных координатах описывается уравнением: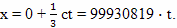
Мировую линию EB звезды, которая является целью путешествия в координатах системы отсчета связанной с эфиром, описывается уравнением: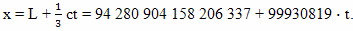
Путешественник движется к цели со скоростью v = 2/3 c относительно наблюдателя с Земли, а Земля, относительно эфира со скоростью w = 1/3 c. Скорость путешественника относительно эфира определяем по формуле Лоренца для сложения скоростей: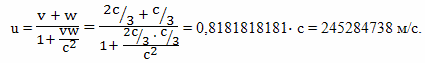
Двигаться путешественник начинает из начала координат по мировой линии AB, поэтому его положение можно рассчитать по формуле: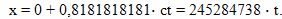
Теперь, зная формулы мировых линий, можно рассчитать координаты события B.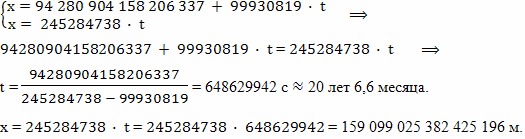
С точки зрения наблюдателя, который находится в системе отсчета мирового эфира, полет космического корабля к звезде занял двадцать с половиной лет. Но время на космическом корабле при быстром движении, согласно теории Лоренца, идет замедленно, поскольку он, и все, что есть на борту, взаимодействует с эфиром.
Рассчитаем время, которое пройдет по корабельным часам: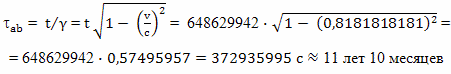
Результат точно такой же, как и в предыдущем примере.
Из события B с координатами t = 648629942 c и x = 159 099 025 382 425 196 м космический корабль движется в событие C. Его скорость, относительно эфира можно рассчитать так: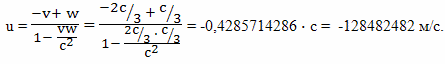
Мировая линия BC описывается формулой: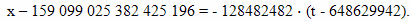
Координаты события C, расположенного на пересечении мировых линий AC и BC, можно рассчитать по уравнению:
Итак, с точки зрения наблюдателя, который, как мы предположили, находится в системе отсчета физического эфира, от момента старта ракеты до завершения путешествия, прошло больше 33 лет. Но, если мы предполагаем, что Земля двигалась относительно эфира, то ход часов на Земле должен был быть замедленным. И собственное время на Земле можно рассчитать по формуле: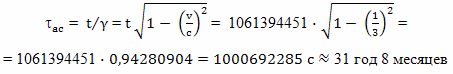
Что в точности совпадает с расчетом, выполненным для случая, когда предполагалось, что Земля неподвижна относительно эфира.
Ну, и, наконец, рассчитаем время, которое прошло по часам путешественника, когда он возвращался на Землю. Относительное замедление хода времени в данном случае составит: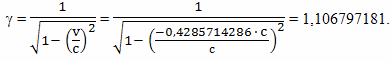
Разницу по времени между событиями B и С с точки зрения наблюдателя, неподвижного относительно эфира, можно определить просто как разность временных координат этих событий: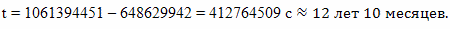
А на часах путешественника между этими событиями прошло время: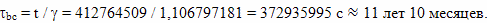
То есть, абсолютно такое же время, как в случае, когда предполагалось, что Земля покоится относительно эфира.
Итак, еще раз посмотрим результаты расчетов.
1. Земля неподвижна относительно эфира.
- Время, прошедшее на Земле: taс = 1 000 692 284 с ≈ 31 год 8 месяцев
- Полет к звезде: τab = 372935995 с ≈ 11 лет 10 месяцев
- Полет обратно: τbc = 372935995 с ≈ 11 лет 10 месяцев
- Время путешествия: τab + τbc = 745871990 ≈ 23 года 8 месяцев.
2. Земля движется относительно эфира.
- Время, прошедшее на Земле: taс = 1 000 692 284 с ≈ 31 год 8 месяцев
- Полет к звезде: τab = 372935995 с ≈ 11 лет 10 месяцев
- Полет обратно: τbc = 372935995 с ≈ 11 лет 10 месяцев
- Время путешествия: τab + τbc = 745871990 ≈ 23 года 8 месяцев.
Таким образом, ни брат домосед, оставшийся на Земле, ни брат путешественник, который совершил путешествие к звезде, анализируя показания своих часов, не смогут определить, движется Земля относительно эфира или нет. Что поделаешь, физическая иллюзия. И эта физическая иллюзия касается всех физических явлений, а не только показаний часов. Согласно предположению Лоренца, никаким из известных физикам экспериментом невозможно установить движение наблюдателя относительно эфира.
И, как позднее это сделал Альберт Эйнштейн, для теории эфира Лоренца можно выделить определенные принципы.
- Принцип наблюдаемого равноправия всех инерциальных систем отсчета. Результаты физических экспериментов не зависят от того, в какой из инерциальных систем отсчета они выполнены.
- Принцип наблюдаемого постоянства скорости света. Измерение скорости света в любой из инерциальных систем отсчета и в любом направлении дает одинаковый результат.
- Дополнительно. Наблюдаемое равноправие всех инерциальных систем отсчета и наблюдаемое постоянство скорости света является результатом "физической иллюзии", возникающей в результате взаимодействия эфира с движущимися объектами.
Как видно из этих принципов, в теории Лоренца различаются наблюдаемые результаты физических экспериментов, которые испытывают влияние "физической иллюзии", и действительные результаты физических экспериментов, которые в силу влияния "физической иллюзии" наблюдателям недоступны. Согласно теории эфира Лоренца, существует абсолютная система отсчета, связанная с физическим эфиром, но эта система отсчета не выделена среди прочих и обнаружить ее невозможно.
Именно эта двойственность теории эфира Лоренца подвергалась критике группы физиков, которые называли себя физиками-релятивистами. Это направление возникло в физике во второй половине девятнадцатого века, а его создателем и главным теоретиком был физик и философ Эрнст Мах. Главным аргументом физиков релятивистов в споре с Лоренцем было утверждение о том, что нет никаких законов природы кроме тех, которые можно обнаружить при помощи физических экспериментов. И, если физический эфир принципиально невозможно обнаружить при помощи физических экспериментов, то следует считать, что его не существует. Но до 1905 года физикам-релятивистам не удавалось создать физическую теорию, которая бы смогла объяснить обнаруженные в конце девятнадцатого века явления без предположения о существования физического эфира.
Cледует отметить, что теория эфира Лоренца не содержала явных внутренних противоречий и наблюдаемое замедление хода времени движущихся объектов в этой теории не создавало парадоксов. Основные претензии к этой теории следовали из общефилософских представлений о природе нашей физической Вселенной.
2. Формулировки парадокса близнецов
Итак, в теории эфира Лоренца парадокс близнецов не возникает. Все правильно и логично, хотя явление замедления времени быстродвижущихся объектов действительно необычно. Парадокс был сформулирован лишь после того, как в 1905 году Альберт Эйнштейн опубликовал статью "К электродинамике движущихся тел", в которой сформулировал принципы относительности.
1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения относятся.
2. Каждый луч света движется в "покоящейся" системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом.
Суть предположения Эйнштейна состояла в том, что не только физические наблюдения во всех все инерциальных системах отсчета дают эквивалентные результаты, но еще и все инерциальные системы отсчета эквивалентны физически. Другими словами, Эйнштейн предположил, что все инерциальные системы отсчета физически равноправны, что никакой абсолютной системы отсчета не существует, независимо от того, выделена она или нет.
Следует учитывать и то, что в данной статье Эйнштейн еще не предлагает объяснения механизма относительного замедления хода времени. Такое объяснение он предложил в том же году в статье "Зависит ли инерция тела от содержащейся в нем энергии". Суммируя предположения, сделанные Эйнштейном в этих статьях, можно предложенные им принципы относительности записать так.
1. Принцип физического равноправия всех инерциальных систем отсчета. Все инерциальные системы физически равноправны.
2. Принцип физического постоянства скорости света. Скорость света в любой инерциальной системе отсчета и в любом направлении одинакова.
Дополнительно. Наблюдаемое относительное замедление времени является результатом зависимости инерциальной массы объектов от их энергии (E = mc2).
Эйнштейн усилил принципы, на которых строилась теория эфира Лоренца. Если Лоренц предполагал, что имеет место только наблюдаемая эквивалентность инерциальных систем отсчета, то Эйнштейн предположил не только наблюдаемую, но и физическую эквивалентность инерциальных систем. Если Лоренц предполагал, что имеет место, только наблюдаемое постоянство скорости света, то Эйнштейн предположил не только наблюдаемое постоянство скорости света, но и действительное физическое постоянство скорости света для любой инерциальной системы отсчета. В. Л. Гинзбург в статье "Кто и как создал теорию относительности" пишет:
"Лоренц и Пуанкаре понимали этот принцип лишь как утверждение о невозможности заметить равномерное движение тела относительно эфира. Перейти отсюда к рассмотрению всех инерциальных систем отсчета как совершенно равноправных (такова современная формулировка принципа относительности) можно без особого труда, только если понимать преобразования Лоренца как имеющие смысл перехода к движущейся системе отсчета". [16 стр. 367]
Но именно такая редакция принципов относительности, послужила основой для создания множества парадоксов теории относительности. В частности, парадокса близнецов.
Повторно рассмотрим ситуацию, которая уже была описана в первой главе. Два брата близнеца расстаются на космодроме, один из них остается на Земле, а другой отправляется в большое космическое путешествие. Брат путешественник быстро набирает скорость, и затем летит на звездолете с постоянной скоростью, сравнимой со скоростью света, к звезде расположенной за десяток световых лет от Земли, а затем, точно так же возвращается обратно. На Земле братья близнецы встречаются, и их ожидает сюрприз. Оказывается, что один из них, который летал в космос, постарел лет на двадцать, а другой, который оставался на Земле, ... ну скажем, лет на тридцать.
Не только наблюдаемая, но и физическая эквивалентность всех инерциальных систем отсчета, предполагает, в первую очередь, эквивалентность хода времени. И тогда, возникает вопрос.
Согласно первому принципу относительности, все системы отсчета эквивалентны и, следовательно, время в них течет одинаково, тогда почему при встрече показания часов брата домоседа и брата путешественника различны?
Это и есть основная формулировка парадокса близнецов.
В такой формулировке остается один неучтенный фактор - время ускорения брата путешественника, для того, чтобы исключить его влияние, можно специально подчеркнуть, что ускоряется брат путешественник очень быстро. Именно в этой трактовке это замечание имеет смысл, в формулировке, предложенной Эйнштейном, особого значения оно не имеет. Но именно этот фактор и был использован физиками-релятивистами для объяснения парадокса близнецов. То есть, основная концепция решения парадокса близнецов сводится к тому, что в ускоренной системе отсчета физические процессы протекают не так, как в инерциальной, а поэтому, на них нельзя распространить первый принцип относительности. И, поскольку перемещение брата путешественника включает в себя участки ускоренного движения, то к ней в целом неприменим первый принцип относительности.
Но, если бы все было НАСТОЛЬКО просто, то не было бы смысла писать эту статью. После принятия изложенной выше концепции, объясняющей парадокс близнецов, возникает масса нюансов. Начать можно хотя бы с того, что понятие "инерциальная система отсчета" это такая же это абстракция, как абсолютно белое тело или абсолютно ровная поверхность, и, строго говоря, совершенных "инерциальных систем отсчета" не существует. Существуют только похожие на них ускоренные системы отсчета.
Ускоренное движение характерно для окружающего нас мира. Движение некоторых тел, на которых воздействие окружающей среды, влияние магнитных полей, давления газа или света, и т.п. мало, можно считать практически инерциальным, хотя фактически оно таковым не является. В реальном мире можно считать инерциальными слабо ускоренные объекты. Но здесь важен критерий, по которому, в зависимости от величин, действующих на тело ускорений, промежутка времени, на котором определена задача, и, возможно, ряда других параметров, выносится суждение о том, можно ли считать движение тела инерциальным или все же, оно должно быть признано ускоренным.
Согласно общей теории относительности, инерциально движущееся тело перемещается в пространственно-временном континууме по, так называемой, геодезической линии. Например, примерно по таким линиям движутся спутники вокруг Земли, или Земля вокруг Солнца. В данном случае, геодезическая линия, это траектория свободно падающего в гравитационном поле объекта. Космонавт, который находится в невесомости, движется по геодезической линии и однозначно является инерциальной системой отсчета. Ну, если не считать действия на него магнитных полей, которое слабо, но все же существует. Но вот, к примеру, брат близнец, оставшийся на Земле, таким объектом точно не является. Двигаться по геодезической линии в пространственно-временном континууме ему мешает поверхность Земли, которая постоянно давит на него снизу. Таким образом, находясь на поверхности Земли, брат домосед постоянно испытывает ускорение 1g относительно траектории свободно падающего тела. Планету в целом можно считать инерциально движущимся телом, но, находящийся на ее поверхности человек, таковым не является. Насколько корректно, и почему корректно, считать его инерциально движущимся объектом?
Двигаясь с ускорением 1g в космическом пространстве в течение 4-5 лет, объект может достичь скоростей близких к скорости света. Это очень просто рассчитать. Четыре года по часам космонавта это примерно 126230400 с. Двигаясь в одном направлении в пространстве с постоянным собственным ускорением 1g = 9,8 м/с2 объект достигнет скорости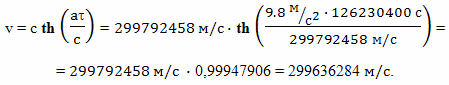
Даже в примере, рассмотренном в прошлой главе, мы ограничились скоростью 2/3 световой, относительно наблюдателя на Земле, а за четыре года по собственным часам ускорения величиной 1g космонавт достигнет скорости более 0,999 от скорости света.
Для того чтобы достигнуть скорости 2/3 от скорости света, с ускорением 1 g, потребуется собственное время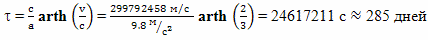
И таких участков ускорения во время путешествия будет ровно 4. То есть, чуть больше 3-х лет брат путешественник при таком режиме полета будет находиться под действием ускорения 1g. А его брат, который остался на поверхности Земли, будет двигаться относительно траектории свободно падающего тела с ускорением 1g все тридцать с лишним лет.
Но опыты показывают, что время у наблюдателя на Земле идет практически так же, как у космонавта, вращающегося вокруг Земли по круговой орбите. Небольшое различие в ходе ускоренных часов на поверхности Земли и часов инерциально движущегося вокруг Земли космонавта в нашем случае несущественно и полностью объясняется влиянием гравитационного поля Земли. То есть, у наблюдателя на Земле с достаточно большой точностью время идет как в инерциальной системе отсчета.
Так почему брат путешественник, который испытал меньшее ускорение, чем его брат, который остался на Земле, испытал большее замедление времени? Ответ может быть только один. Дело не только в ускорении, но еще и в ряде других факторов. Каких именно факторов, мы предметно и детально рассмотрим в следующих главах.
А теперь, вернемся к формулировке парадокса близнецов. Этот парадокс с самого начала был сформулирован так, чтобы исключить влияние ускоренных участков полета брата путешественника. Для этого, предполагалось, что ускорение происходит очень быстро, практически одним импульсом. Но и этого оказалось недостаточно, физики-релятивисты объяснили "потерянное время" как раз этими короткими импульсами. И для того, чтобы полностью исключить влияние ускорения на ход времени, был разработан вариант парадокса близнецов, который больше известен как "метод трех инерциальных систем".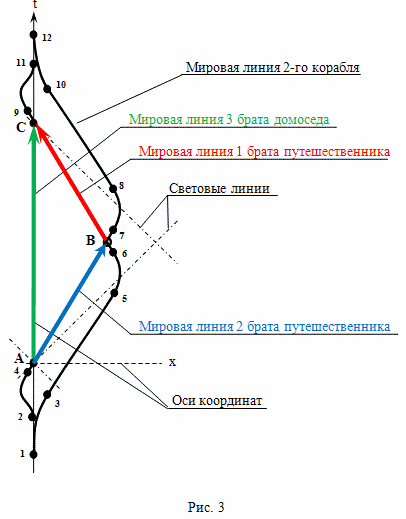
В этом варианте парадокса, нам потребуются трое близнецов, но главными действующими лицами будут их часы. Двое братьев летят в космос, ну а третий домосед. Основан этот вариант парадокса близнецов на том утверждении, что часы могут быть точно синхронизированы между собой, если они находятся практически в одной точке пространства, даже если движутся они с разными скоростями. Схема полета в этом случае может выглядеть так (рис.3).
Вначале в точке 1 с Земли стартует первый брат путешественник и сразу разгоняется к цели путешествия. Второй брат путешественник стартует немного позже в точке 2 и разгоняется в обратном направлении, затем разворачивается, и разгоняется к цели путешествия так, что мимо Земли космический корабль пролетает с отключенными двигателями, являясь инерциальной системой отсчета. В событии A пролетающий мимо Земли космический корабль получает сигнал точного времени от третьего брата близнеца, оставшегося на Земле, устанавливает свои часы по Земле и продолжает лететь равномерно и прямолинейно в направлении цели путешествия.
Некоторое время первый и второй братья близнецы летят в одну сторону и с одинаковой скоростью. Первый брат летит с некоторым опережением. В точке 5 он начинает торможение, а затем ускоряется в направлении Земли и в точке B встречается со вторым братом, который летит ему навстречу. В момент наибольшего сближения второй брат путешественник посылает первому брату путешественнику сигнал точного времени со своих часов. Далее первый брат путешественник летит равномерно и прямолинейно до самой Земли и в точке C посылает сигнал точного времени третьему брату близнецу, который оставался на Земле.
Получается эстафета, в которой точное время кочует от третьего брата ко второму, затем к первому и возвращается снова к третьему. И третий брат обнаруживает разницу между показаниями своих часов и переданных ему данных точного времени. Все часы предполагаются идентичными, и ход времени во всех физических системах предполагается одинаковым, поэтому, естественно, возникает парадокс.
Согласно первому принципу относительности, все системы отсчета эквивалентны и время в них течет одинаково, тогда почему сумма длительностей последовательных инерциальных процессов AB и BC, следующих непрерывно один за другим, меньше длительности инерциального процесса AC?
Принятое в современной физике решение этого парадокса вкратце состоит в том, чтобы ввести понятия "времени сдвига" между разными системами координат и "времени перескока" для перехода от одной системы отсчета к другой. Рассчитывая время при помощи этих величин, можно получить правильные результаты. И в логике выкладок, обосновывающих необходимость введения таких величин, не нужно искать подвоха. Гораздо интереснее другое. А именно, детальный анализ той модели мира, той трактовке принципов относительности, при которых использование таких концепций как "время сдвига" и "время перескока", не только допустимо, но и необходимо.
Еще одна формулировка парадокса близнецов, которая принадлежит Альберту Эйнштейну. Вкратце, эту формулировку можно дать в следующей редакции:
Пока брат путешественник равномерно и прямолинейно движется к цели, а потом, точно так же, возвращается обратно, в его системе отсчета замедленно идет время на Земле. Тогда почему, при возвращении на Землю, больше времени пройдет у брата домоседа?
В статье Эйнштейна "Диалог по поводу возражений против теории относительности" эта формулировка звучит так:
"Здесь-то и возникает трудность. Согласно принципу относительности, весь процесс должен протекать совершенно одинаково, если его представить в системе K', которая движется вместе с часами U2. По отношению к системе K' движутся назад и вперед часы U1, тогда как часы U2 все время остаются в покое. Но отсюда следует, что по окончании движения часы U1 должны отставать от часов U2, в противоположность сделанному выше выводу". [1 стр. 618]
На что стоит обратить внимание. Парадокс близнецов это парадокс, основанный на принципах относительности в редакции Эйнштейна, основанный на утверждении о физической эквивалентности, равноценности всех инерциальных систем отсчета. Но в формулировке предложенной Альбертом Эйнштейном этого нет. Утверждение о физической эквивалентности заменено на заведомо более слабое утверждение об эквивалентности физических наблюдений. А утверждение о том, что из физической эквивалентности инерциальных систем отсчета следует, что перемещавшиеся часы должны идти точно так же, как и часы неподвижные, заменено на совершенно другое утверждение. Эйнштейн утверждает, что с точки зрения системы отсчета U1 должны замедленно идти часы в системе отсчета U2, а с точки зрения системы U2 должны замедленно идти часы в системе отсчета U1. А это, согласитесь, совсем не то же самое, что утверждение о том, что часы должны идти одинаково.
Очевидно, Эйнштейн намеренно ушел от основной формулировки парадокса близнецов. Зачем? Эйнштейн использовал формулировку, которая вплотную подводит к решению парадокса близнецов в терминах координатной одновременности. То есть, вместо того, чтобы решать парадокс близнецов в его оригинальной формулировке, Эйнштейн адаптировал формулировку парадокса к использованному им математическому аппарату теории относительности. Но, при такой адаптированной формулировке, возникает масса дополнительных вопросов.
Например, Эйнштейн пишет: "По отношению к системе K' движутся назад и вперед часы U1". И многие могут подумать, будто часы U1, то есть, часы брата близнеца оставшегося на Земле, действительно движутся вперед и назад, буквально, как это написано в статье Эйнштейна. Следует иметь в виду, что речь идет только об относительном времени, которое зависит от выбора системы отсчета.
Дадим слово Максу Борну.
"Каждая из систем с равным правом может претендовать на то, что время показываемое именно ее часами, правильное, ибо каждая может утверждать, что именно она покоится, поскольку все физические законы проявляются в обеих системах в одной и той же форме. Но, когда двое утверждают нечто такое, что по своему смыслу может принадлежать лишь одному, мы должны заключить, что бессмысленно само утверждение.
Не существует такой вещи, как абсолютная одновременность".
И, в случае ускоренно движущегося брата близнеца, это утверждение весьма актуально. Нет никаких оснований считать, что именно система отсчета ускоренно движущегося брата близнеца правильно описывает действительный ход времени на Земле. И, следовательно, нет никаких оснований утверждать, что время на часах брата, оставшегося на Земле, действительно "двигалось вперед и назад" по отношению к часам брата путешественника.
Брат путешественник, находясь на значительном расстоянии от Земли, непосредственно наблюдать относительное движение вперед и назад времени на Земле не может, и недостающие данные он получает при помощи расчетов, которые базируются на определенных физических предпосылках, и, с которыми можно поспорить, используя концепции теории относительности.
Например, если принять расчеты ускоренно движущегося брата путешественника как физический факт, то, в тот момент, когда он ускоряется в направлении Земли, Земля начинает удаляться от него со скоростью, которая может в десятки и сотни раз превышать скорость света. И это неотъемлемая часть того же самого наблюдения и тех же расчетов, которые приводят к выводу о том, что время на Земле движется ускорено, относительно космического корабля. Об этом не упоминают физики-релятивисты, описывая парадокс близнецов, но это существенная деталь. Естественно, возникает вопрос о том, насколько корректна такая методика, и насколько можно верить результатам, полученным с ее помощью.
В этой же статье, Эйнштейн высказывает предположение о влиянии на ход ускоренно движущихся часов брата путешественника гравитационного потенциала. Это предположение принято в современной физике как догма, но оно далеко не бесспорно. Можно предложить целый ряд мысленных экспериментов и реальных физических экспериментов, которые опровергают это предположение.
И есть еще одна формулировка парадокса близнецов, которую совершенно необходимо обсудить. В статье Эйнштейна, брат путешественник соотносит время, прошедшее на космическом корабле со временем на Земле. Но Земля далеко и полученные таким образом результаты сомнительны. А ведь можно соотносить ход времени на космическом корабле с ходом времени в пространственной сетке, построенной для системы отсчета наблюдателя с Земли.
Технически это может выглядеть так. По маршруту космического корабля от Земли к звезде располагаем множество станций, оборудованных часами точного времени, неподвижными относительно Земли и синхронизированными с Землей в системе отсчета наблюдателя с Земли. Такой вариант парадокса близнецов известен под названием "метод частой сетки".
Подобную сетку станций теоретически можно сделать сколь угодно частой. И, хотя этот проект фантастичен, сложности с ним связанные, исключительно технические. И в этом варианте парадокса близнецов, он может быть сформулирован так:
В течение всего полета в одном направлении (в инерциальной, и в ускоренной его части), а затем, в течение всего полета в обратном направлении (в инерциальной, и в ускоренной его части), брат путешественник наблюдает расположенные по пути следования станции. И, он видит, что точно синхронизированные с ходом времени на Земле часы всех этих станций, когда он пролетает мимо них, идут медленнее, чем часы на космическом корабле. Тогда почему, когда он возвращается на Землю и встречается со своим братом, оказывается, что у него прошло меньше времени, чем у его брата, который оставался на Земле?
Рассмотрение парадокса близнецов с такой точки зрения, очень полезно для понимания явления в целом, хотя бы потому, что оказывается, что на возникающую разницу во времени, между часами брата путешественника и брата домоседа, ускоренные участки полета влияют в меньшей степени, чем участки полета с постоянной максимальной скоростью. А значит, реальное относительное замедление времени близнеца путешественника происходит вовсе не на участках ускорения.
Парадокс близнецов это, прежде всего, логическое противоречие, основанное на неправильных изначальных предпосылках. И все представленные выше формулировки этого парадокса в той или иной мере содержат ложные данные, которые приводят к парадоксальному результату. И решение парадокса должно состоять в том, чтобы показать, какие именно среди данных не соответствуют истине, то ли утверждение о равноправности всех инерциальных систем отсчета, то ли описание дальнейшего сценария путешествия.
3. Приближенный расчет большого космического путешествия
Методику приближенного расчета полета брата путешественника в космос на значительное расстояние от Земли, предлагает М. В. Сажин в книге "Теория относительности для астрономов" в разделе 4.1.1. Эта методика, в свою очередь, основана на алгоритме, приведенным Альбертом Эйнштейном в статье "Диалог по поводу возражений против теории относительности". Отличие лишь в том, что М. В. Сажин рассматривает случай, когда скорость движения брата путешественника относительно Земли достаточно велика, для того чтобы проявлялись эффекты релятивистской физики, но, все же, значительно меньше скорости света. Такой подход позволяет ему использовать для расчетов более простые приближенные формулы.
В частности, по формулам приближенного вычисления, в математике в некоторых случаях допустима следующая замена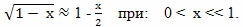
Используя эту замену, М. В. Сажин вместо формулы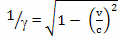
использует ее упрощенный аналог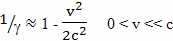
На этом основании, вместо формулы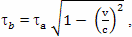
где: τa - время путешествия к звезде и обратно по часам наблюдателя с Земли, τb - время путешествия к звезде и обратно по часам путешественника, Сажин записывает приближенную формулу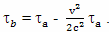
Время участков ускоренного движения М. В. Сажин принимает пренебрежимо малой величиной и не учитывает их в расчетах. И делает вывод: с точки зрения наблюдателя с Земли часы путешественника должны отстать на величину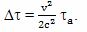
Затем, Сажин рассматривает происходящее с точки зрения путешественника. Двигаясь равномерно и прямолинейно, путешественник считает, что замедленно идет время на Земле, то есть, используя ту же самую упрощенную формулу, можно записать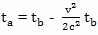
и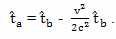
где: ta - время, прошедшее на Земле, по расчетам путешественника, за время его полета к Звезде; ˆta - время, прошедшее на Земле, по расчетам путешественника, за время его полета обратно; tb - собственное время путешественника, прошедшее за время его полета к Звезде; ˆtb - собственное время путешественника, прошедшее за время его полета обратно. Таким образом, Сажин использует следующую систему обозначений. Измерения, сделанные в системе отсчета брата домоседа (Земля) он обозначает величинами с индексом a. Измерения, сделанные в системе отсчета брата путешественника (космический корабль) он обозначает величинами с индексом b. Время путешествия "туда" и "обратно" Сажин обозначает греческой буквой τ. Время путешествия "туда", обозначает буквой t. А время путешествия "обратно" буквой t c "шапочкой".
Однако, кроме этих участков, на которых путешественник двигался равномерно и прямолинейно, рассматривая происходящее с точки зрения брата путешественника, следует учитывать участки ускоренного движения. Само время ускорения мало и членом, зависящим от разницы скоростей (пропорциональный член) на всех участках ускоренного движения можно пренебречь. Сажин специально отмечает, что при ускоренном движении вблизи Земли потенциальный член тоже мал, и им можно пренебречь. Другое дело при ускорении вблизи цели путешествия. Здесь влияние члена обусловленного влиянием гравитационного потенциала становится существенным.
Для изменения направления движения, то есть изменения скорости с величины +v (движение к звезде) на величину -v (движение с такой же по величине скоростью обратно), в течение времени разгона 2tр, требуется ускорение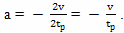
Величина относительного замедления времени τп, согласно современной трактовке теории относительности, обусловлена гравитационным полем, возникающим при ускоренном движении путешественника (потенциальный член)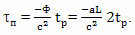
где: Ф - гравитационный потенциал; a - величина ускорения; L - расстояние между Землей и ускоренно движущимся братом путешественником, 2tр - удвоенное время разгона, складывается из времени торможения у звезды и времени разгона обратно.
Подставляем в эту формулу значения ускорения a и расстояния L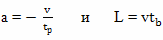
и получаем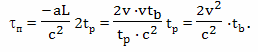
Учитывая, что путь к звезде и обратно по часам путешественника составит величину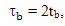
можно рассчитать общее время, прошедшее на Земле с точки зрения брата путешественника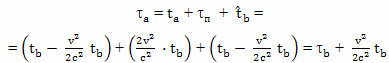
То есть, согласно этому расчету, у брата, оставшегося на Земле, пройдет время на величину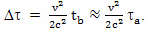
больше, чем у брата совершившего космическое путешествие.
На самом деле, если выполнить более громоздкий, но точный расчет, в результате должны получиться две совершенно одинаковые величины.
М. В. Сажин предлагает упрошенную методику расчета, а, следовательно, эта методика имеет ограниченное практическое применение. Оценим область ее применимости в зависимости от скорости движения брата путешественника. Для этого сравним величину относительного замедления времени и величину относительной ошибки, возникающей при применении приближенной формулы при разных скоростях.
В приведенной ниже таблице (Таблица 1) для скоростей равных 0,5, 0,2, 0,1, 0,05, и 0,01 от скорости света приведен расчет точности вычислений при применении данной методики. Для значения коэффициента относительного замедления времени γ, рассчитанного по точной формуле, приведен также релятивистский эффект замедления хода времени в процентах. Далее приводится коэффициент γ, рассчитанный по упрощенной формуле, а потом величина относительной ошибки расчетов δ.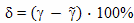
Сравнение величин релятивистского эффекта и величин ошибки расчетов позволяет оценить применимость методики для разных скоростей.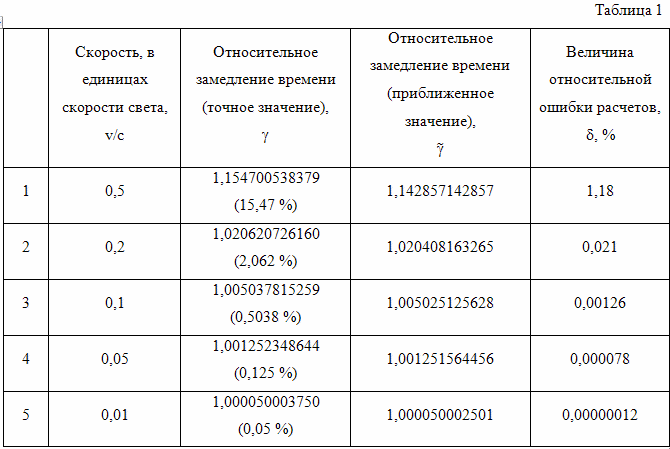
Как видно из этой таблицы, с уменьшением величины скорости растет точность вычислений по методу, который использует М. В. Сажин. Но при скоростях сравнимых со скоростью света, точность вычислений невелика даже для простых технических расчетов. При скорости равной половине скорости света относительная ошибка расчетов всего в 15 раз меньше эффекта вызываемого относительным замедлением хода времени.
С другой стороны, ближайшая обнаруженные звезда Проксима Центавра расположена на расстоянии порядка 4,22 световых лет от Земли, около 4·1016 м. Совершить путешествие к такой звезде и обратно в течение человеческой жизни со скоростью меньше чем 0,2 скорости света невозможно. Таким образом, практическое применение данной методики очень сильно ограничено только областью ближайших звезд и только скоростью порядка 0,2 световой.
А теперь произведем расчет с конкретными значениями величин. Рассмотрим вариант полета, который показан на рисунке 4. Скорость движения брата путешественника относительно брата домоседа на участках BC и EF одинакова. Ускорение на участках AB, CD, DE и FG одинаково. Все интервалы времени участков ускорения с точки зрения наблюдателя с Земли равны. Все интервалы собственного времени участков ускорения брата путешественника, тоже равны. Предположим, что скорость полета равна v = 50 000 000 м/с. Расстояние до цели путешествия примем L = 5·1016 м.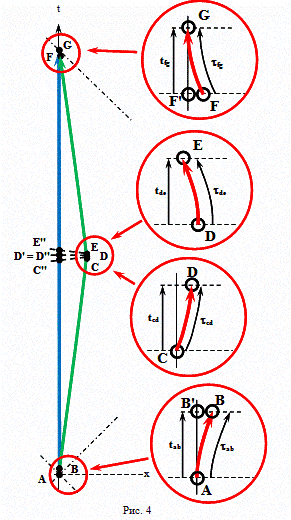
Отметим, что оба путешественника проводят наблюдения на основе метода радарной одновременности. То есть, если один брат наблюдает, что часы другого идут в γ раз медленней, это означает, что оценка одновременных событий была произведена по методу радара.
Вначале, рассмотрим происходящее с точки зрения наблюдателя с Земли.
По часам наблюдателя с Земли, путешествие космического корабля с братом путешественником к звезде займет время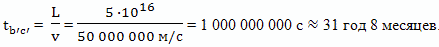
Здесь: ta'd' - время полета брата путешественника к цели по часам брата оставшегося на Земле; td'g' - время полета брата путешественника, обратно, по часам брата оставшегося на Земле.
И, точно такое же время займет путь обратно: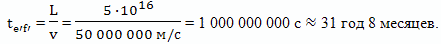
месяцев.
Следовательно, все путешествие, при условии, что брат путешественник не будет задерживаться возле цели путешествия, а сразу полетит обратно, займет около 63 лет и 4 месяцев. В течение всего этого времени брат домосед будет наблюдать, что часы брата путешественника идут замедленно
Обратную величину коэффициента относительного замедления времени можно рассчитать по формуле Лоренца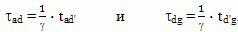
Здесь: τad - собственное время брата путешественника, то есть, время по часам космического корабля, которое пройдет во время путешествия к цели; τdg - собственное время брата путешественника, которое пройдет во время путешествия обратно; γ - величина относительного замедления времени, при наблюдении движущихся объектов по методу радарной одновременности. Здесь и далее, символом t я буду обозначать время в системе координат брата домоседа, а символом τ - собственное время брата путешественника.
Для обоих братьев во время полета равномерно и с постоянной скоростью, величина γ одинакова. То есть, брат, оставшийся на Земле, считает, что время идет замедленно в γ раз у путешественника, а путешественник считает, что время идет замедленно в γ раз на Земле.
Обратную величину коэффициента относительного замедления времени 1/γ можно рассчитать по формуле Лоренца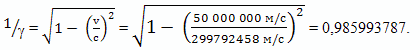
Откуда находим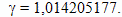
Следовательно, по часам брата путешественника, в течение полета в одну сторону пройдет время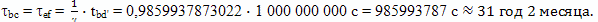
А все путешествие займет 2·985993787 с = 1 971 987 574 с.
То есть, после полета брат путешественник оказался младше брата домоседа на величину 2 000 000 000 с - 1 971 987 574 с = 28 012 426 с ≈ 10,6 месяца.
Это точная формула, но сейчас мы проведем расчет по методике изложенной М. В. Сажиным и используем эти данные для оценки абсолютной ошибки вычислений.
По приближенной формуле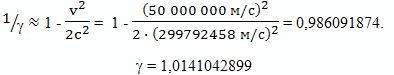
Различие в значениях коэффициентов, полученных по разным формулам, уже в четвертой значащей цифре после запятой. По этой формуле получается, что по часам брата путешественника полет к цели путешествия, как и полет обратно, займет собственное время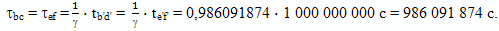
Ошибка в расчетах по предложенной Сажиным методике, при полете в одну сторону, составит почти 105 секунд, это примерно 27 часов. Или 54 часа в обе стороны. Мелочь, по сравнению с 63 годами времени на Земле.
А по часам вернувшегося из путешествия брата, пройдет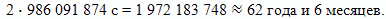
Используя приближенную формулу, мы найдем, что брат путешественник оказался младше брата домоседа на 2 000 000 000 с - 1 972 183 748 с = 27 816 252 с ≈ 10,6 месяца.
Когда мы измеряем срок полета в месяцах, такая небольшая погрешность вычислений даже не будет заметна. Но и полет совершался на скоростях значительно меньших, чем скорость света. Но в нашем случае важным еще является то, что релятивистский эффект, то есть, разность между показаниями часов, оказывается значительно больше, чем присущая используемой методике ошибка.
Временем необходимым для разгона и торможения мы в этом расчете пренебрегли. Насколько это оправдано? Для оценки времени разгона до скорости, примерно равной 0,2 от скорости света, вполне подойдут формулы из классической физики. При комфортном для космонавтов длительном ускорении космического корабля с величиной 1g = 9,81 м/с2, то есть, с таким же ускорением, какое испытывает человек стоя на Земле, разгон до скорости 50 000 000 м/с займет время примерно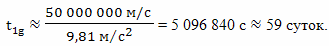
Здесь следует отметить, что с точки зрения классической физики, человека стоящего на Земле можно считать неподвижным, а, ускоренно движется падающее на Землю тело, на которое действует гравитация. С точки зрения общей теории относительности, под действием гравитации изменяется геометрия пространственно-временного континуума, и свободно падающее тело движется в этом искривленном пространстве по прямой линии без ускорения. И, как следует из мысленного эксперимента с физиками в закрытом помещении, нахождение на поверхности планеты физически эквивалентно ускоренному движению в космическом пространстве. А вот проекция мировой линии инерциально движущегося в поле гравитации тела на евклидово пространство, может выглядеть, например, эллипсом, как орбиты спутников вокруг Земли.
Таких участков ускоренного движения (разгона и торможения) на протяжении полета будет четыре, и 8 месяцев, по сравнению с более чем 63 годами, действительно не очень большая величина. Но эта величина сравнима с релятивистским замедлением времени, а, следовательно, этим временем пренебречь в расчетах уже не получится. Для того чтобы приблизится к заданному в формулировке парадокса близнецов условию, что космический корабль разгоняется очень быстро, "импульсом", то есть, так, чтобы временем разгона можно было пренебречь, необходимо разгоняться значительно быстрее, например, с ускорением в 100g. При этом время одного разгона составит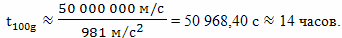
И тогда, общее время ускоренного движения за время путешествия составит около 56 часов, то есть, время сравнимое с величиной ошибки методики расчетов. Какие "гравикомпенсаторы" будет применяться на космическом корабле для того, чтобы сохранить жизнь и здоровье брата путешественника при таком ускорении, я не знаю, но примем в рассчетах величину ускорения 100g.
Теперь, рассмотрим происходящее с точки зрения брата путешественника.
С точки зрения брата путешественника, который тоже использовал метод радарной одновременности, пока он летел равномерно и прямолинейно, замедленно шли часы у его брата домоседа. И, за то время, пока он летел к звезде (отрезок BC) и когда он возвращался, по его расчетам на Земле прошло время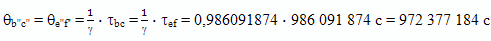
Здесь и дальше, расчетная величина прошедшего на Земле времени, полученная братом путешественником на основе метода радарной одновременности, будет обозначаться греческой буквой θ, чтобы не путать ее со временем, идущим по часам на Земле, и с собственным временем путешественника.
В прямоугольной декартовой системе отсчета брата путешественника, одновременность будет выглядеть иначе, чем в системе отсчета брата домоседа. Например, подлетая к событию C, он определит как одновременные события C и C''. А начав двигаться обратно от события E, он определит как одновременные события E и E''. Интервал AC'' это время, которое прошло на Земле, по расчетам путешественника, при полете к цели. Интервал E'F это время, которое прошло на Земле, по расчетам путешественника, при полете обратно. А вот интервал между событиями C'' и E'' как раз и есть "потерянное" время в формулировке парадокса близнецов в редакции Эйнштейна
По предположению Эйнштейна, когда путешественник изменяет свою скорость, на участке CDE, время на Земле идет ускоренно, относительно космического корабля и интервал времени между событиями C'' и E'' значительно больше, чем между событиями C и E.
Участки ускоренного движения AB и FG.
По официальной версии теории относительности, разница между наблюдениями братьев близнецов возникает потому, что один из братьев близнецов движется ускоренно и создаваемый им гравитационный потенциал ускоряет ход времени на Земле.
Для расчета величины такого относительного ускорения хода времени можно использовать формулу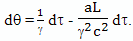
Вывод этой формулы будет дан позднее. В этой формуле: dθ - небольшой промежуток времени, которое проходит на Земле, по расчетам брата путешественника, γ - коэффициент относительного замедления времени, вызванного разницей скоростей, a - собственное ускорение космического корабля, L - расстояние от Земли до космического корабля, c - скорость света, dτ - небольшой промежуток собственного времени брата путешественника,
Подробный вывод этой формулы будет дан в следующих главах. Ее правая часть состоит из двух членов, первый из них принято называть пропорциональным, а второй потенциальным. Пропорциональный член отражает относительное замедление времени связанное с разностью скоростей, а потенциальный член отражает влияние на ход времени гравитационного потенциала.
Для того чтобы рассчитать прошедший на Земле промежуток времени, пока космический корабль двигался ускоренно, нужно найти интеграл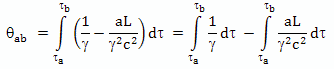
в котором величины γ и L функции от собственного времени τ.
Пропорциональный член в этом уравнении заведомо меньше времени разгона корабля τр = τab = 50968 с, которым мы пренебрегаем, потому, что величина 1/γ все время разгона была равна или меньше единицы. А, следовательно, его тоже можно в данном расчете отбросить, как и время разгона.
Расстояние, на которое удалится от Земли космический корабль, за время разгона можно оценить по формуле классической физики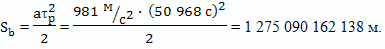
Очевидно, также,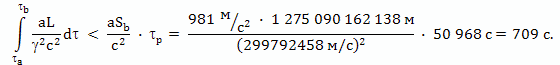
Так, что этой величиной тоже можно пренебречь, как и в целом, временем θab.
Аналогичный вывод можно сделать и по отношению к завершающему участку полета космического корабля FG. По этой причине, поправкой к ходу времени ускоренно движущегося брата путешественника на участках AB и FG в данном расчете можно не учитывать.
Участки ускоренного движения CD и DE.
В этом случае, расстояние от Земли составляет величину примерно L = 5·1016 м. Причем, эта величина незначительно меняется в ходе торможения на участке CD, поэтому величину интервала времени между событиями С'' и D'', прошедшими на Земле, с точки зрения брата путешественника, пока он двигался ускоренно, с достаточной точностью можно вычислить по формуле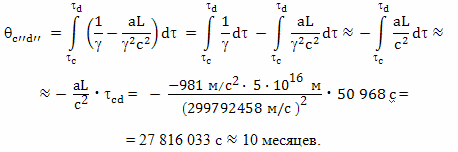
Величина γ2, являясь функцией собственного времени, плавно нелинейно меняется от 1 до величины 1,0284075, в среднем она значительно ближе к 1, чем величина 1,014, поэтому, этой величиной мы пренебрегаем.
Обратите внимание! Здесь ускорение a направлено в обратную сторону, в направлении Земли, а поэтому, взято со знаком минус.
Аналогичный вывод можно сделать относительно участка DE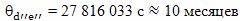
Итог.
С точки зрения брата домоседа, путешествие должно было занять 200 000 000 секунд.
Суммируем величины интервалов времени, прошедших на Земле с точки зрения брата путешественника: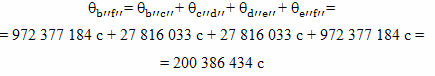
Ошибка вычислений составила 386434 секунды, около 4 суток, и это в большей степени разница между величинами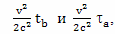
в приведенной М. В. Сажиным методике расчетов. Эта ошибка изначально заложена в данной методике, но имеет тот же порядок, как ряд величин, которыми мы в расчете пренебрегали, а, поэтому, допустима.
Комментируя эти выкладки, М. В. Сажин пишет:
"Этот расчет демонстрирует отсутствие "парадокса близнецов" в релятивистской физике".
Но, на самом деле, подобный расчет демонстрирует непротиворечивость только математической модели, а еще, дает надежду на то, что при записи формул не допущены грубые ошибки, и ничего больше.
Первоначальная формулировка парадокса близнецов в достаточной мере опровергается одной фразой:
"Теория утверждает равноценность только всех галилеевых (неускоренных) систем координат, т. е. таких систем координат, по отношению к которым в достаточной мере изолированные материальные точки движутся прямолинейно и равномерно. Такой системой координат является, конечно, система K, но не ускоряемая время от времени система K'".
Действительно, влияние ускоренных участков полета в первоначальной формулировке парадокса близнецов не было учтено, и большинство физиков считает этот факт достаточным для опровержения парадокса близнецов. Остается только доказать, что влияние ускоренного движения на ход времени действительно имеет место, и действительно таково, как это нужно для непротиворечивости теории относительности, и этого достаточно для объяснения парадокса. Либо, нужно, например, доказать, что на ускоренное движение тоже распространяется принцип относительности, по крайней мере, в отношении хода времени. И это будет доказательством того, что в современной теории относительности дано неверное объяснение парадокса близнецов.
4. Абсолюты теории относительности
В теории относительности эфир, как среда, взаимодействующая с движущимися частицами и "делающая" их массивнее, инертнее и замедляющая ход времени движущихся объектов, отсутствует. В этой теории нет абсолютной системы отсчета, относительно которой замедлялись бы другие системы отсчета. Зато в этой теории есть другой абсолют, инерциальные системы отсчета, то есть, системы отсчета связанные с телами, которые движутся равномерно и прямолинейно. В теории относительности все инерциальные системы равноправны и физически эквивалентны, следовательно, объективно, время во всех инерциальных системах отсчета должно идти одинаково. Именно на принципе относительности, утверждающем равноправие инерциальных систем отсчета в такой трактовке, и был изначально построен парадокс близнецов.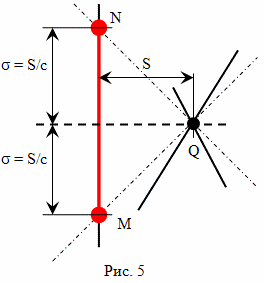
Но, какими физическими экспериментами можно подтвердить (или опровергнуть), что время в других инерциальных системах идет точно так же, как и некой одной из них, выбранной нами? Обозначим выбранную нами инерциальную систему прямой мировой линией MN (рис. 5). И пусть на некотором отдалении от этой мировой линии располагается некоторое событие Q, принадлежность которого к какой-то определенной системе отсчета спорно. Такое может быть, например, если событие Q это столкновение двух массивных элементарных частиц, которое породило множество более мелких частиц, разлетающихся от события Q в разных направлениях и с разными скоростями.
Таким образом, событие Q можно связать с множеством различных систем отсчета, которые будут двигаться по отношению к мировой линии MN со скоростями -c < v < +c. И в каждой из этих систем отсчета событие на мировой линии MN, одновременное событию Q, будет определено по методу радарной одновременности по-своему. Общим, у всех этих способов определения событий одновременных событию Q на линии MN, будет то, что они будут находиться между событиями M и N. Таким образом, точность, с которой мы можем определить событие, одновременное событию Q, равна 2σ = 2L/c, где L- расстояние от прямой MN до события Q, измеренное по перпендикуляру к прямой линии NM, c - скорость света.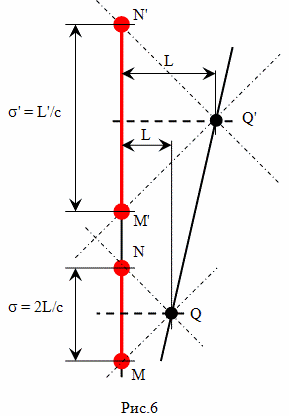
Если теперь, придерживаясь этой концепции оценивать ход времени на мировой линии инерциально движущегося тела MN и на мировой линии инерциально движущегося тела QQ', то абсолютно точно можно утверждать, что промежутку времени между событиями Q и Q', соответствует промежуток времени t, продолжительность которого не менее, чем интервал между событиями N и M', и не более, чем интервал между событиями M и N'. А такой точности недостаточно для того, чтобы однозначно выбрать между следующими вариантами:
-время на прямой MN идет в γ раз быстрее, чем на прямой QQ',
-время на прямой MN идет в γ раз медленнее, чем на прямой QQ'
-или что в обеих инерциальных системах отсчета ход времени одинаков.
Каждый из перечисленных вариантов связан с определенной методикой и определенной системой координат. Первый вариант связан с асимметричным обменом световыми сигналами по методике радарной одновременности в системе координат MN. Второй вариант связан с асимметричным обменом световыми сигналами по методике радарной одновременности в системе координат QQ'. Третий вариант связан с симметричным обменом световыми сигналами в полярной системе координат с началом отсчета в точке пересечения прямых MN и QQ'.
Каждая из этих методик имеет свои достоинства и недостатки, и однозначный выбор между ними невозможен, а принципиально иные способы определения одновременности событий современной физике неизвестны. И это означает невозможность экспериментального подтверждения того, является ли относительное замедление времени только наблюдаемым явлением или это реально существующее явление.
Согласно теории эфира Лоренца, для наблюдателя, принадлежащего абсолютной системе отсчета, относительное замедление хода времени это объективно существующее и наблюдаемое явление, для остальных наблюдателей - суперпозиция объективно существующего замедления времени и физической иллюзии. В противовес теории Лоренца, принципы относительности, предложенные Эйнштейном, изначально предполагали именно полную физическую эквивалентность инерциальных систем отсчета, что подразумевает объективно одинаковый ход времени.
Здесь стоит привести цитату из книги В. А. Угарова "Специальная теория относительности":
"И все же самое главное в теории относительности, вопреки ее названию, - это совсем не относительность различных величин, т. е. их зависимость от выбора системы отсчета. Суть теории относительности как раз в обратном. Теория относительности показывает, что законы природы в инерциальных системах отсчета не зависят от выбора системы отсчета, не зависят от положения и движения наблюдателя, а результаты измерений в различных системах отсчета могут быть сопоставлены. Говоря философским языком, теория относительности подчеркивает объективный характер законов природы, а вовсе не относительность знаний". [5, стр. 36]
И, с этой точки зрения, объективно, время во всех инерциальных системах отсчета идет одинаково, а относительное замедление времени это эффект появляющийся в результате использования определенной методики наблюдений. Впрочем, в источниках по теории относительности, встречается и другая точка зрения, и к ней я еще вернусь.
Несмотря неопределенность синхронизации удаленных друг от друга часов, существует достаточно много физических экспериментов, позволяющих получить некоторую определенность относительно свойств хода времени в удаленных системах отсчета и/или в системах отчета движущихся относительно Земли. Когда события удалены друг от друга, определить их одновременность можно только относительно, то есть, привязываясь к определенной системе отсчета, и в разных системах отсчета определение одновременности будет различным. И, как уже отмечалось выше, разброс определения одновременности заведомо будет равен Ђσ =ЂL/c. Из этого следует, что одновременность событий, которые расположены достаточно близко (L→0), можно определить с достаточно большой точностью, а если события совпадают, их одновременность определяется абсолютно точно, независимо от принадлежности к той или иной системе отсчета наблюдателей и физических явлений, связанных с этими событиями.
На основании астрономических наблюдений, мы с большой точностью можем утверждать равномерность хода времени в удаленных от Земли системах отсчета, как неподвижных относительно Земли, так и движущихся. Для такого вывода достаточно исследовать спектр удаленных от Земли звезд и галактик. На том же основании можно утверждать равномерность хода времени на Земле, относительно всех прочих удаленных от Земли объектов.
Так же, на основании наблюдений, можно утверждать, что во всех удаленных от Земли инерциальных системах отсчета, скоростью которых относительно Земли можно пренебречь, ход времени совпадает с ходом времени на Земле. Для такого вывода достаточно учесть равномерность хода времени и провести наблюдения в течение времени T>>σ.
И это только самые очевидные эксперименты.
Рассматривая с точки зрения упомянутых выше свойств времени большое космическое путешествие, можно отметить следующее. Еще до старта с Земли космического корабля, находясь в одной точке пространства, братья близнецы могут абсолютно точно синхронизировать как показания своих часов, так и скорость их хода. Затем, после того, как, ускорившись, космический корабль будет двигаться равномерно и прямолинейно к цели путешествия, определение хода времени на космическом корабле станет относительным, то есть, при помощи физических экспериментов определить, идут ли часы у братьев близнецов одинаково или одни часы спешат относительно других, будет невозможно.
По мере удаления от космического корабля от Земли, неопределенность синхронизации часов σ будет увеличиваться пропорционально увеличению расстояния от Земли до космического корабля. На этом участке полета космического корабля, экспериментальное определение соотношения хода часов на космическом корабле и на Земле может быть только относительным. И здесь мы можем опираться только на принцип относительности, который постулирует равнозначность всех инерциальных систем отсчета. Или наоборот, можно постулировать наличие физической иллюзии и пользоваться теорией эфира Лоренца, и считать замедление хода времени одного из братьев, относительно другого, объективным фактом.
Ситуация меняется принципиально, когда космический корабль начинает двигаться в направлении Земли. С этого момента расстояние между Землей и космическим кораблем начинает уменьшаться и, вместе с ним, начинает уменьшаться неопределенность синхронизации часов σ. И, в определенный момент времени, точность определения одновременных моментов времени становится достаточной для того, чтобы утверждать, что по часам одного из братьев прошло больше времени, чем по часам другого. И вновь, абсолютно точно соотнести показания своих часов близнецы смогут, встретившись в одной точке пространства, после завершения путешествия.
На каждом из участков полета определение хода времени на Земле и на космическом корабле было относительным, но, в конце путешествия, мы получили абсолютный результат - разницу между ходом часов на Земле и ходом часов на космическом корабле за время всего путешествия. Собственно говоря, парадокс близнецов и был сформулирован только для того, чтобы определить, на каком этапе большого космического путешествия образуется абсолютная разница хода времени. Не относительная, а именно абсолютная!
В формулировке парадокса близнецов, которую дал Эйнштейн, упущено главное. Для анализа принципа относительности, утверждающего равноправность инерциальных систем отсчета, не столь важно относительное замедление времени, и не столь важно наблюдаемое замедление времени, и не столь важны расчетные величины, которые получены на основе метода радарной одновременности. Здесь принципиально важен именно этап формирования абсолютной разницы в показаниях часов.
Эйнштейн утверждает, что разница между часами брата путешественника и брата домоседа возникает потому, что при ускоренном движении возникает гравитационный потенциал и "часы идут тем быстрее, чем больше гравитационный потенциал в том месте, где они находятся". А когда космический корабль ускоряется в направлении Земли, гравитационный потенциал часов, находящихся на Земле, оказывается значительно больше, чем гравитационный потенциал космического корабля, следовательно, часы, расположенные на Земле, должны идти быстрее, чем на космическом корабле.
Основываясь на этом утверждении, можно предположить, что абсолютная разница хода часов образуется именно на участках ускоренного движения. И, хотя Эйнштейн пишет том, что ускоряется ход времени на Земле, относительно космического корабля, мы же знаем, что маневры космического корабля где-то далеко в космосе, не могут реально повлиять на ход времени на Земле. Следовательно, речь идет не об абсолютном ускорении хода времени на Земле, а об ускорении хода времени на Земле относительно часов космического корабля. То есть, подразумевается, что на самом деле не ускоряется время на Земле, а, в результате ускоренного движения, замедляется ход времени на космическом корабле. Причем, это замедление должно быть не только относительным, но и абсолютным, то есть, таким, чтобы после встречи и сверки хронометров, близнецы обнаружили разницу.
В примере, который мы рассматривали в прошлой главе, разница между показаниями часов брата домоседа и брата путешественника составила 10,6 месяца. Оценим возможность того, что абсолютное замедление времени образовалась именно на участках ускоренного движения. На участках ускоренного движения AB и FG оценить возможность образования абсолютной разницы во времени можно по наблюдениям хода времени на Земле (рис. 7).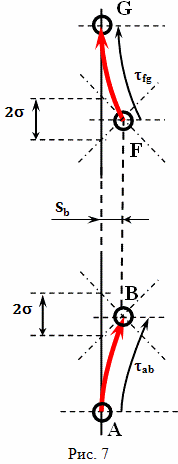
Как следует из расчетов, выполненных в прошлой главе, в событии B и в событии F космический корабль будет находиться на расстоянии примерно S = 1 275 090 162 138 м от Земли, следовательно, разброс определения одновременности составит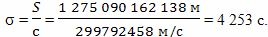
Кроме того, при расчетах в прошлой главе мы пренебрегли величиной порядка 709 секунд. То есть, суммарная абсолютная разница между собственным временем брата близнеца брата путешественника никак не может быть больше величины около 1000 секунд при разгоне к цели путешествия и около1000 секунд при торможении возле Земли.
Цель путешествия звезда, скорость которой относительно Земли очень мала, и ее можно считать равной нулю. Как было показано выше, путем наблюдений можно установить, что ход времени на этой звезде точно соответствует ходу времени на Земле. И, поскольку, подлетая к этой звезде, космический корабль тормозится и разгоняется точно так же, как это было возле Земли (рис. 7), абсолютная разница на участках CD и DE так же составит никак не больше, чем по 1000 секунд, если сравнивать ход часов с инерциальным телом, мировая линия которого проходит через событие D и параллельна мировой линии Земли. Если же, использовать для синхронизации мировую линию инерциально движущегося тела, которое проходит через события C и D, то абсолютная разница на участке CDE составит значительно меньше, чем величина 2·709 с = 1418 с.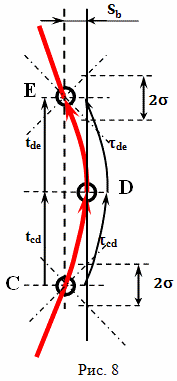
В итоге, имеем следующее. Общее собственное время ускоренного движения составляет 4·50 968 с = 203 872 с. Абсолютная разница между ходом времени на Земле и ходом времени на космическом корабле, при этом, заведомо не могла превышать величины 2·1000 с + 2·709 с = 2000 с + 1418 с. = 3418 с. Абсолютное замедление хода времени больше этой величины, можно было бы обнаружить, наблюдая за разгоном и торможением космического корабля с Земли и звезды, которая является целью путешествия. И эта величина заведомо меньше разницы во времени примерно в 10,6 месяца, образовавшейся в результате путешествия. А, следовательно, абсолютная разница в ходе времени могла образоваться только на участках равномерного и прямолинейного полета и, лишь в незначительной степени, на участках ускоренного движения.
5. Полет до середины пути
Рассмотрим еще один вариант полета (вариант 2), за основу которого взят полет, рассмотренный в третьей главе (вариант 1). Для наглядности изобразим оба варианта полета на одном рисунке (рис. 9). Различие между первым и вторым вариантами полета состоит в том, что во втором варианте путешественник долетает только до середины пути, некоторое время остается в этой точке, неподвижный, относительно Земли, а затем, возвращается обратно. Предположим, что второй вариант путешествия рассчитан так, чтобы его продолжительность по часам брата домоседа в точности равнялась продолжительности полета в первом варианте.
Для расчета используем ту же методику, что и в предыдущей главе.
Итак, вначале, рассмотрим происходящее с точки зрения наблюдателя с Земли.
Половина пути до цели первого варианта, это расстояние 2,5 · 1016 метров и его брат путешественник, двигаясь со скоростью 50 000 000 м/с преодолеет за время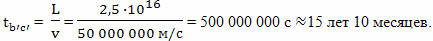
Точно такое же время займет полет обратно на Землю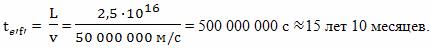
Временем разгона и торможения, как и в прошлом расчете, пренебрегаем. По условиям, от момента старта до момента возвращения на Землю, прошло такое же время, как и в первом варианте, то есть,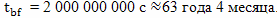
Из этого времени 2 · 500 000 000 секунд брат путешественник двигался прямолинейно и равномерно со скоростью 50 000 000 м/с. Временем ускоренного движения пренебрегаем и остается 1 000 000 000 секунд по времени по часам наблюдателя с Земли, когда путешественник неподвижно висел в космосе на расстоянии 2,5 · 1016 метров от Земли.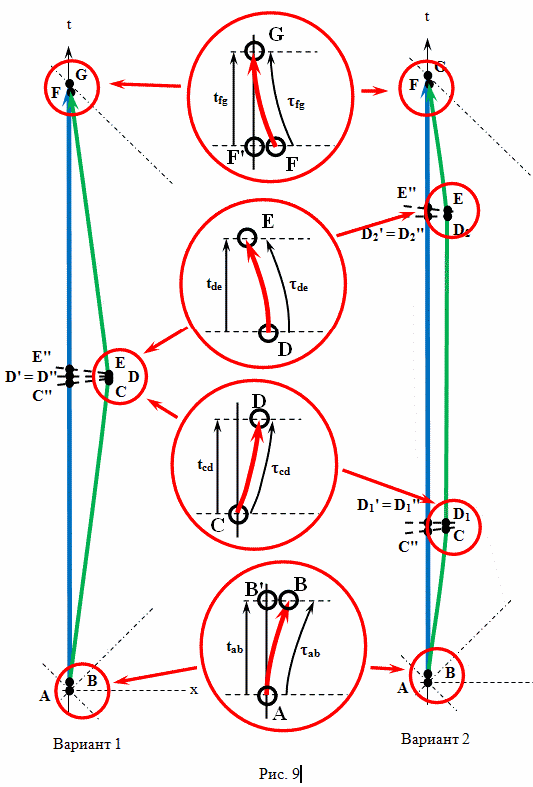
Поскольку во время "висения" путешественник был неподвижен относительно Земли и не ускорен, время у него шло точно так же как и на Земле, и по его часам тоже должно было пройти время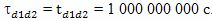
На участках BC и EF наблюдатель с Земли отмечает, что время у путешественника идет замедленно. Скорость движения путешественника точно такая же, как и в первом варианте, а поэтому, коэффициент относительного замедления времени, рассчитанный по методике приведенной М. В. Сажиным, остается таким же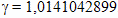
Поэтому мы легко можем найти, что по часам, установленным на космическом корабле, перелет от Земли до точки "висения" и перелет обратно заняли одинаковое время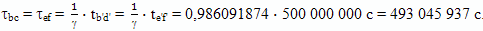
Таким образом, продолжительность всего полета по часам путешественника складывается из следующих интервалов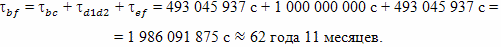
Разница между показаниями часов брата путешественника и брата домоседа, по этим расчетам, должна составить 13 908 125 секунд ≈ 5,3 месяца.
Теперь рассмотрим этот полет с точки зрения брата путешественника.
Пока путешественник движется равномерно и прямолинейно на участках BC и EF, проводя измерения на основе метода радарной одновременности, он обнаружит, что замедленно шло время на Земле и там прошло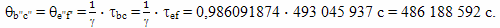
Находясь в точке "висения" на полпути между Землей и звездой, брат путешественник методом радарной одновременности может определить, что ход времени у него и на Земле одинаков, а, следовательно, этот интервал времени будет равен измеренному на Земле и измеренному с Земли для путешественника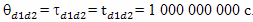
Участки ускоренного движения.
Про участки ускоренного движения вблизи Земли AB и FG можно в точности повторить все то, что было сказано в прошлой главе для первого варианта полета, и я повторяться не буду. Для участков ускоренного движения CD1 и D2E применяем формулу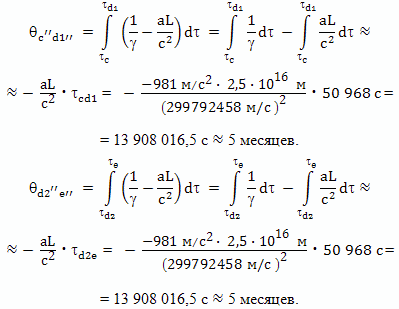
В итоге получаем.
Суммируем величины интервалов времени, прошедших на Земле с точки зрения брата путешественника: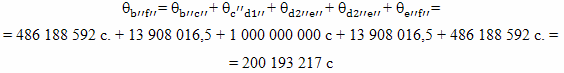
Ошибка вычислений составляет 193 217 секунд, около 2 суток.
Теперь сравним оба варианта. Второй вариант путешествия отличается от первого тем, что двигатели космического корабля включались в другое время и на другом расстоянии от Земли. Величина ускорения космического корабля и время движения с ускорением были одинаковы, причем, одинаковы с точки зрения обоих наблюдателей. В результате, в первом варианте путешествия космический корабль отдалился от Земли на максимальное расстояние 5·1016 м, а во втором варианте путешествия космический корабль отдалился от Земли на максимальное расстояние 2,5·1016 м. В первом случае, по часам брата путешественника прошло на 10,6 месяца меньше, чем у брата домоседа. А во втором случае, по часам брата путешественника прошло на 5,3 месяца меньше. Разница между показаниями часов братьев сократилась ровно в два раза.
Подобные расчеты можно произвести для множества вариантов полета с "зависанием" на разном расстоянии от Земли, но так, чтобы скорость движения v, величина ускорения a и время разгона tр были одинаковы. И во всех этих вариантах абсолютная разница между показаниями часов брата домоседа и брата путешественника, по итогам полета, окажется прямо пропорционально зависящей от расстояния, на которое удалится от Земли путешественник, скорости его движения относительно Земли и коэффициента относительного замедления времени.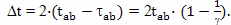
Убежденные сторонники теории эфира Лоренца ничего необычного в этом не найдут, более того, сочтут этот факт подтверждением теории эфира. А все потому, что, согласно этой теории, замедление хода времени в γ раз у брата путешественника возникало, когда он двигался относительно эфира, то есть, относительно физического трехмерного пространства в течение времени 2tab. А если, в системе отсчета движущегося относительно физического пространства - эфира, брату путешественнику кажется, что замедленно идет время на Земле, то это только физическая иллюзия. В теории относительности эта же формула трактуется иначе. Преобразуем ее.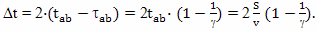
Используя приближенную формулу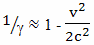
делаем подстановку и находим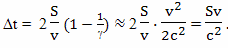
Используем еще одну приблизительную формулу из классической физики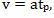
в которой a - ускорение, tр - время движения с ускорением. И получаем результат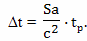
Это приближенная формула для случая c >> v >> 0. Точная формула немного сложнее, но и она будет содержать в качестве аргументов величину ускорения a, время ускорения tр, и расстояние S от наблюдателя на Земле, до ускоренного наблюдателя на космическом корабле. И, как было сделано выше, зависимость абсолютной разницы хода часов от величины S, можно подтвердить непосредственно расчетами.
В такой интерпретации, источником абсолютной разницы в ходе часов является ускоренное движение космического корабля. Эйнштейн об этом пишет так:
"Все существующие во Вселенной звезды следует считать участвующими в создании гравитационного поля, поскольку в процессе ускорения координатной системы K' они ускоряются по отношению к последней и могут индуцировать гравитационное поле подобно тому, как ускоренно движущиеся электрические заряды индуцируют электрическое поле". [1 стр. 622]
Предположение о том, что силы инерции обусловлены не свойствами физического пространства, как предполагала теория эфира, а вызываются суммарным гравитационным полем, создаваемым всеми массивными телами физической Вселенной, было высказано еще в девятнадцатом веке и принадлежит Эрнсту Маху, основателю релятивистской физики. Эйнштейн, который присоединился к физикам релятивистам в начале двадцатого века, это предположение несколько модифицировал для того, чтобы объяснить воздействием всех массивных тел не только силы инерции, но и относительное изменение хода времени при ускоренном движении.
И, вот здесь есть нюанс. Мы, конечно же, реалисты и понимаем, что маневры небольшого космического корабля, где-то в глубинах Вселенной, не могут оказать существенного влияния на ход времени на Земле. И, если речь идет об ускорении хода времени на Земле, относительно космического корабля, то, скорее всего, это означает замедление хода времени на самом космическом корабле. Следовательно, можно предположить, что создаваемое всеми массивными объектами Вселенной глобальное гравитационное поле воздействует непосредственно на ход времени ускоренного тела. Но, если это так, то такое воздействие не должно зависеть от того, в какой части физической Вселенной находится ускоряемое тело, не должно зависеть от того, в каком направлении ускоряется тело, не должно зависеть от его массы и целого ряда других параметров. Индуцированное общим гравитационным полем замедление времени должно зависеть только от величины ускорения и времени, в течение которого действовало ускорение.
В приведенной выше формуле видно, что эти условия не соблюдаются. Величина абсолютного замедления времени оказывается зависящей от того, как далеко от инерциального наблюдателя, находится ускорено движущийся космический корабль. Но сам Альберт Эйнштейн и не утверждает, что ускоренное движение космического корабля вызывает абсолютное замедление хода времени на нем. Нет, он пишет буквально:
"ускоряются по отношению к последней и могут индуцировать гравитационное поле подобно тому, как ускоренно движущиеся электрические заряды индуцируют электрическое поле". [1 стр. 622]
То есть, Эйнштейн пишет о том, что окружающие ускоренно движущуюся систему отсчета удаленные объекты ускоряются по отношению к ней и индуцируют гравитационное поле, ускоряющее ход времени. И, чем дальше от ускоренно движущейся системы отсчета находится объект, тем более сильное индуцированное гравитационное поле на него действует. То есть, центром и источником этого индуцированного поля является сама ускоренная система отсчета, именно она создает это поле, ускоряющее ход времени в окружающем пространстве.
Впрочем, насчет "ускоряются по отношению к последней", это тоже не совсем верно. Если вокруг ускоренной системы отсчета действительно создается индуцированное гравитационное поле, то оказывается, что оно зависит не только от расстояния между объектами, но еще и от направления в котором ускоряется система отсчета. Поэтому поле получается несимметричным и в одних направлениях оно вызывает относительное ускорение времени, в других относительное замедление времени, а есть даже области, в которых относительное время даже меняет свое направление на противоположное. Но об этом поговорим в следующей главе.
В статье Эйнштейна "Диалог по поводу возражений против теории относительности", лояльно настроенный Критик задает Релятивисту вопрос:
"Но разве не является это гравитационное поле чем-то чисто фиктивным? Ведь его существование вызвано только выбором системы координат. Истинные же гравитационные поля всегда создаются массами и не могут быть устранены подходящим выбором системы координат. Как же можно поверить, что некоторое явно фиктивное поле оказывает влияние на ход часов?" [1 стр. 620]
И его собеседник Релятивист, вполне в духе философского релятивизма Эрнста Маха отвечает:
"различать реальное и нереальное для нас не имеет смысла",
и далее:
""физическая реальность" соответствует вовсе не гравитационному полю, взятому самому по себе, но только этому же полю вместе с другими явлениями. поэтому нельзя сказать ни того, что гравитационное поле само по себе есть нечто "реальное", ни того, что оно "чисто фиктивно"". [1 стр. 621]
Здесь Релятивист уходит от вопроса о реальности индуцированного гравитационного поля, хотя вопрос совсем не праздный и для определения реальности этого поля есть вполне вещественный критерий. Если все это только математический прием, описывающий только относительный ход времени в ускоренно движущейся системе отсчета, но не влияющий на абсолютное замедление времени, то это фиктивное поле. А, если ускорено движущаяся система отсчета вызывает действительное абсолютное изменение хода времени, то это есть "нечто реальное".
Итак, ход времени в инерциальной системе отсчета это абсолют постулируемый принципами относительности и маловероятно, что ход времени на Земле действительно зависит от каждого из множества разнообразных ускоряемых систем отсчета во всей Вселенной. Ход времени на участках разгона и торможения не может быть существенно замедлен, имеется в виду не относительное, а абсолютное замедление. В этой и прошлой главе были приведены два из целого ряда доказательств этого факта. А на участках равномерного и прямолинейного движения, согласно принципам относительности, все физические системы физически равноправны. Предположение о том, что время не относительно, а абсолютно, в одной инерциальной системе отсчета шло быстрее, чем в другой, противоречит основным принципам теории относительности.
А все это означает, что "индуцированное гравитационное поле" действительно фиктивная величина. Реально это "гравитационное поле" не влияет на ход времени ни в инерциальной, ни в ускоренной системах отсчета, и отражает только изменения, которые происходят с координатными переменными при повороте системы отсчета.
"Доказательство" парадокса близнецов это искусная иллюзия. На каждом этапе этого доказательства Эйнштейн оперирует только с относительными замедлениями времени, если быть точным, то даже не с наблюдаемым ходом времени на Земле, а с некой расчетной величиной. Вначале расчет производится с точки зрения наблюдателя с Земли, затем с точки зрения наблюдателя расположенного на космическом корабле. И нет ничего удивительного в том, что эти вычисления сходятся. А вот самое главное, с точки зрения парадокса близнецов, источник появления абсолютной разницы в ходе часов, так и не показан. Ведь относительное замедление (ускорение) времени, на участках разгона и торможения, как это было показано выше, на действительный ход времени в обеих системах отсчета никак не влияет.
6. Поворот системы отсчета
Когда одна система отсчета движется ускоренно, связанная с ней координатная система поворачивается в пространстве Минковского. По этой причине, результирующий относительный ход времени состоит из двух составляющих, которые принято называть пропорциональной и потенциальной. Пропорциональная составляющая пропорциональна коэффициенту относительного замедления времени γ и зависит от мгновенной скорости объекта относительно системы координат. Термин потенциальная составляющая связан с предположением Эйнштейна о том, что ускоренное движение приводит к возникновению гравитационного потенциала и изменению хода времени. В случае, когда система отсчета движется равномерно и прямолинейно, потенциальная составляющая равна нулю, независимо от того, движется наблюдаемый объект ускоренно или равномерно и прямолинейно. Рассмотрим вначале именно этот случай.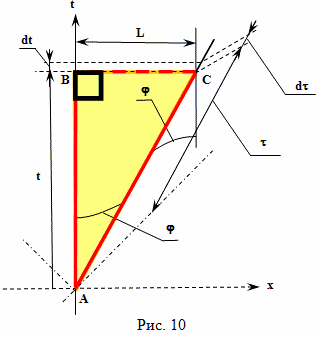
Построим схему в системе отсчета наблюдателя с Земли, мировая линия которого совпадает с осью координат t. Пусть некий объект движется равномерно и прямолинейно с некоторой скоростью v, в выбранной системе отсчета. В некотором событии A, мировые линии наблюдателя с Земли и движущегося относительно него объекта пересеклись, затем объект стал удаляться от Земли. Используя метод радарной одновременности, наблюдатель с Земли может рассчитать, что когда на Земле наступит событие B, этот объект удалится от Земли на расстояние L = vt и окажется в событии C.
Получившийся в пространстве Минковского прямоугольный треугольник ABC во многих случаях удобно рассматривать именно как геометрическую фигуру и использовать для расчетов гиперболические функции. В этом треугольнике угол при вершине B бесконечный прямой, и это следствие применения метода радарной одновременности. Величину угла φ, при вершине A, можно найти, зная скорость движения объекта в выбранной системе координат v, через гиперболический арктангенс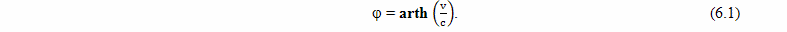
Из этой формулы можно вывести соотношение катетов этого треугольникаили 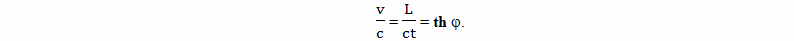
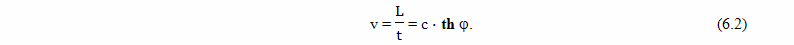
Отношение интервала времени наблюдателя с Земли между событиями A и B к интервалу собственного времени объекта, между событиями A и C, то есть, отношение прилежащего к углу φ катета треугольника ABC к его гипотенузе, можно выразить через гиперболический косинус угла φ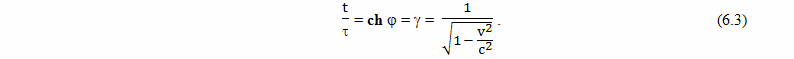
Отношение противолежащего к углу φ катета треугольника к его гипотенузе можно выразить через гиперболический синус угла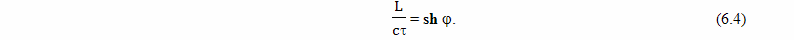
Через гиперболические функции можно выразить относительный ход времени в дифференциальной форме. То есть, если наблюдатель с Земли, используя метод радарной одновременности, измеряет интервалы времени, прошедшего на космическом корабле, то небольшой интервал времени собственного времени на космическом корабле dτ он соотнесет с небольшим интервалом времени на Земле dt, следующим образом: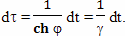
Наблюдатель на космическом корабле, тоже использующий для определения хода времени на Земле метод радарной одновременности, построит свой прямоугольный треугольник ACD иначе (рис. 11). В этом треугольнике в пространстве Минковского прямой угол C, хотя на проекции из пространства Минковского на евклидову плоскость, то есть, на диаграмме Минковского, этот угол выглядит как острый.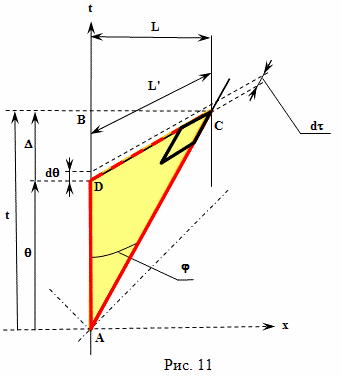
Этот наблюдатель, измеряя при помощи метода радарной одновременности ход времени на Земле, придет к выводу, что замедленно в раз идет время на Земле. Чтобы не создавать путаницу, обозначим это расчетное время греческой буквой θ. Тогда, в прямоугольной декартовой системе отсчета связанной с космическим кораблем, будут верны следующие тригонометрические соотношения:и 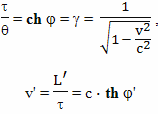
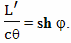
в которых: L' - расстояние между Землей и космическим кораблем в системе отсчета космического корабля для события C; v'= -v - скорость движения Земли относительно космического корабля; φ' = -φ угол наклона мировой линии Земли, относительно мировой линии космического корабля.
Учитывая, что τ = t/γ, легко можно рассчитать, что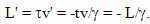
Небольшой интервал времени собственного времени на космическом корабле dτ, при этом, наблюдатель на космическом корабле соотнесет с небольшим интервалом расчетного времени на Земле dθ, следующим образом: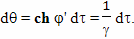
При изменении скорости полета космического корабля, изменяется его система отсчета, то есть, его направление движения в пространстве Минковского, и, соответственно, изменяется связанная с этой системой отсчета система координат. Чаще всего, для описания происходящих событий и процессов в теории относительности используют прямоугольную декартову систему координат. А, при изменении системы отсчета, новую систему координат строят таким образом, чтобы ось координаты времени была касательной к мировой линии, по которой перемещается система отсчета в пространстве Минковского, в том событии, в котором находится объект.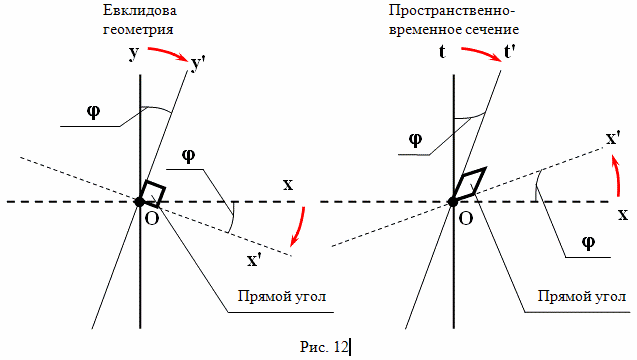
Оси пространственных координат, в прямоугольной системе координат, связаны с осью времени и тоже поворачиваются. Однако, в отличие от евклидового пространства, в поворот осей координат в пространстве Минковского обладает рядом особенностей. Например, при повороте прямоугольной системы координат на евклидовой плоскости, оси x и y поворачиваются в одну сторону (рис. 12). Если ось x поворачивается по часовой стрелке на угол φ и занимает положение x', то ось y поворачивается тоже на угол φ, тоже по часовой стрелке, и занимает положение y'. Соответственно, если ось x поворачивается на угол φ против часовой стрелки, то и ось y поворачивается на угол φ против часовой стрелки.
В пространстве Минковского, при повороте на плоскости прямоугольной системы координат, оси координат поворачиваются в разные стороны. То есть, если ось времени t поворачивается по часовой стрелке на угол φ, то перпендикулярная ей ось пространственной координаты x повернется на угол φ против часовой стрелки. И, соответственно, если ось времени t поворачивается против часовой стрелки на угол φ, то перпендикулярная ей ось пространственной координаты x повернется на угол φ по часовой стрелке. И получившиеся прямые t' и x' тоже будут взаимно перпендикулярны в пространстве Минковского, хотя в отображении на евклидову плоскость, эти прямые будут казаться расположенными под острым углом.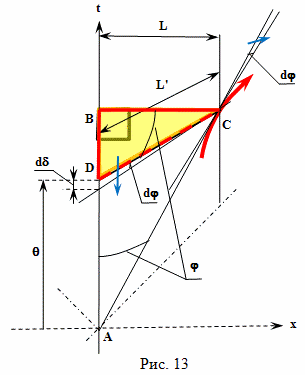
Когда наблюдатель движется ускоренно, его мировая линия в пространстве Минковского искривлена, и координатная ось времени постоянно меняет свое направление и, вместе с ней, поворачиваются пространственные оси координат. Поэтому, при ускоренном движении, при небольшом изменении собственного времени наблюдателя dτ система отсчета поворачивается на небольшой угол dφ и расчетное время одновременного удаленного события, рассчитанного по методу радарной одновременности, изменится на величину dδ (рис. 13). Таким образом, проводя наблюдения за Землей и производя расчеты, путешественник определит, что одновременно с событием C+dτ на космическом корабле произошло событие D-dδ на Земле.
При небольшом изменении величины угла φ изменяются все параметры треугольника ACD кроме прямого угла C. При увеличении скорости на величину dv = f(φ, dφ), тело, двигаясь от Земли равномерно и прямолинейно, достигло бы события С за меньшее время. По этой причине сокащаются все длины сторон треугольника ACD. Соответственно, сокращается расстояние L' от Земли до космического корабля в системе отсчета космического корабля. Чтобы иметь объективные данные об изменении этих величин, следует привязаться к величинам, которые остаются постоянными.
События B, C и D на рисунке 13 образуют прямоугольный треугольник. Наблюдатель на Земле считает одновременными события C и B, наблюдатель с космического корабля считает одновременными события C и D. Разницу во времени между событиями B и D обозначим буквой δ. Для этого треугольника верно следующее тригонометрическое соотношение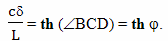
Угол ∠BCD равен углу φ по правилу построения перпендикуляров в пространстве Минковского. Следовательно,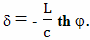
и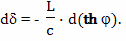
Используем соотношение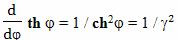
и получаем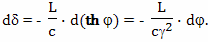
Знак минус означает, что при положительном направлении ускорения космического корабля, точка D смещается в отрицательном направлении.
Угол dφ и собственное время на космическом корабле dτ связаны соотношением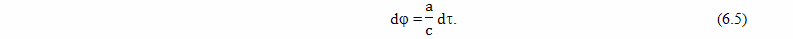
В этой формуле a - собственное ускорение космического корабля, то есть, величина ускорения, которую может измерить находящийся на его борту космонавт. В приведенных здесь расчетах я задаю эту величину постоянной на все время разгона с точки зрения наблюдателя на космическом корабле, то есть, так, чтобы этот наблюдатель все время ощущал постоянное ускорение. При этом, наблюдатель находящийся на Земле, и использующий метод радарной одновременности, будет считать, что с ростом скорости ускорение уменьшается на величину γ. Подставляем это выражение и получаем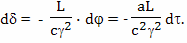
Теперь, учитывая пропорциональный и "потенциальный" члены, находим, что небольшому его промежутку собственного времени космического корабля dτ будет соответствовать небольшой промежуток времени на Земле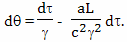
Помним, в этой формуле L - расстояние от Земли до космического корабля в системе отсчета Земли, a - собственное ускорение космического корабля. Приведем эту формулу к классическому виду. Для этого заменим L на γL', то есть расстояние в системе отсчета Земли на расстояние в системе отсчета космического корабля, выведем коэффициент γ за скобки, и получим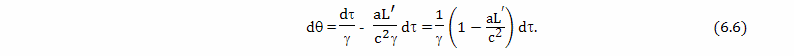
Обычно же, в теории относительности второй множитель в правой части этого уравнения записывается так: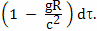
Здесь, величина g трактуется как возникающее на космическом корабле гравитационное ускорение, источником которого являются его двигатели, а величина R трактуется как расстояние от источника гравитации до объекта, на который эта гравитация действует. В нашем случае, это расстояние от космического корабля до планеты Земля. Можно привести достаточно веские возражения против такой интерпретации этих величин.
В случае, который рассматривается в парадоксе близнецов, все происходит в одной пространственно-временной плоскости и некоторые факты не очевидны. Но, если рассматривать более сложные случаи, то можно показать, что величина g не имеет непосредственного отношения к гравитации. Более того, строго говоря, это даже не величина собственного ускорения космического корабля, а просто величина, описывающая динамику изменения расстояния между ускоренным объектом и наблюдателем на Земле d2R/dτ2.
Например, в случае полета по окружности, вокруг инерциального наблюдателя, ускорение, направленное к центру окружности, присутствует, ощущение космонавтами "гравитации" тоже присутствует, но расстояние между инерциальным наблюдателем на Земле и космическим кораблем остается постоянным R=const. Следовательно, равна нулю величина d2R/dτ2 и "потенциальный" член тоже равен нулю. Этот пример достаточно убедительно доказывает, что величина a в формуле 6.6, это не собственное ускорение космического корабля, и не гравитация, действующая на космонавтов, это просто величина той же размерности, что и ускорение, но зависящая только от динамики поворота системы координат относительно удаленного наблюдателя, а не от собственного ускорения.
Формулу 6.6 можно записать и в форме тензорного уравнения. Договоримся, что брат путешественник, находящийся на борту космического корабля, в какой-то момент собственного времени строит систему прямоугольных декартовых 4-координат из той точки-события пространственно-временного континуума, в которой он находится. Так, чтобы координатная ось времени была направлена касательно мировой линии, по которой в пространстве Минковского перемещается корабль, в момент τ=0. Тогда собственные координаты космического корабля в момент τ=0 будут (0, 0, 0, 0).
По логике метода радарной одновременности, одновременными каждому моменту настоящего времени космического корабля будут все события y, для которых координата времени равна нулю, то есть, события с координатами (0, x1, x2, x3). И одно из этих событий, событие X это момент настоящего времени на Земле, определенный по методу радарной одновременности наблюдателем с космического корабля. Для наглядности и упрощения расчетов, всегда можно построить прямоугольную систему 4-координат так, чтобы событие X в настоящий момент находился в плоскости, образованными осями x1 и x2. То есть, так, чтобы xi=(0, x1, x2, 0). Величины элементов x1 и x2 можно выразить через расстояние между космическим кораблем и Землей R, в системе отсчета космического корабля, и углом между направлением на Землю и осью координат x1: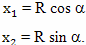
Дополнительно к предыдущему условию, можно сориентировать систему координат так, чтобы проекции ускорения космического корабля на оси x2 и x3 были равны нулю. Тогда ускорение Земли, относительно начала отсчета будет выражено в 3-координатах как aα =(a1, 0, 0).
Если космический корабль движется неускоренно, равномерно и с постоянной скоростью, относительно Земли, и, соответственно, в выбранной системе координат Земля движется относительно космического корабля с постоянной скоростью v = (v1, v2, v3), то в момент собственного времени космического корабля dτ новые координаты одновременного события на Земле X+ Δ, определенные по методу радарной одновременности, будут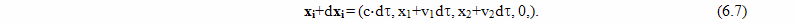
И, при этом перемещении в пространстве Минковского, на Земле должен пройти интервал времени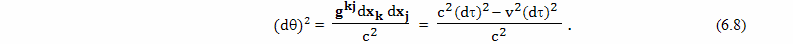
где: v2 = (v1)2 + (v2)2 + (v3)2 - квадрат величины скорости Земли, относительно космического корабля.
Откуда следует: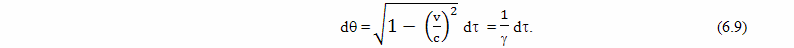
Обратите внимание. Величина относительного замедления хода времени γ не зависит от направления скорости. Но в парадоксе близнецов мы рассматриваем случай, когда скорость направлена вдоль оси x1. Учтем это в дальнейшем.
Если же, космический корабль движется ускоренно, то дополнительно происходит поворот системы координат вместе с системой отсчета на угол dφ в пространственно-временной плоскости образованной координатными осями x0 и x1. И теперь, момент X на Земле будет иметь координаты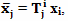
где: Tji - оператор поворота системы отсчета в плоскости x0, x1 на угол dφ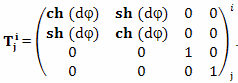
Таким образом, после поворота системы отсчета, координаты события X будут равны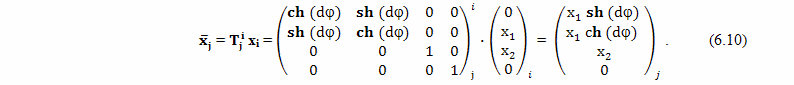
Как видно по нулевому элементу, в новой системе координат, событие X произошло в момент времени −x 0 = x1 sh (dφ). Угол dφ очень мал, поэтому для него с большой точностью можно использовать формулу приближенного вычисления sh φ ≈ φ .
Поэтому координата по времени события X после поворота системы координат будет равна величине: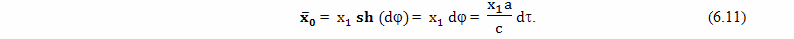
И, по часам космического корабля, это событие должно было произойти в момент времени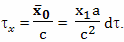
Но, пока происходил этот поворот системы координат, на космическом корабле прошло время dτ и теперь, одновременным ему событием в новой системе координат должно быть событие с координатой времени −y0 = d . Поэтому, с точки зрения наблюдателя на космическом корабле, за время dτ одновременное космическому кораблю событие X сменилось событием Y. По часам космического корабля, между событиями X и Y прошел интервал времени равный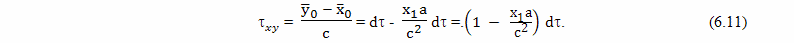
Мировая линия между двумя этими событиями в пространстве Минковского действительная прямая и при повороте системы координат ее форма остается неизменной. А поэтому, также как и в случае с неускоренным движением космического корабля, найти время, прошедшее на Земле между событиями X и Y можно по формуле (6.8), рассчитав координаты этих событий и время, необходимое для перемещения из одного в другое по прямой линии. Но, можно сделать проще.
Используем тот факт, что проекция любого отрезка прямой линии в пространстве Минковского на координатную ось времени в γ раз больше, чем действительная длина этого отрезка. Следовательно, и в системе отсчета космического корабля между событиями X и Y должно пройти время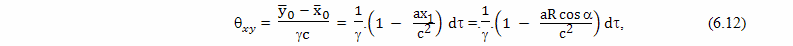
где: α - это угол между направлением на Землю и направлением, в котором "ускоряется" Земля, относительно космического корабля.
Множитель cos α , про который "забывают" буквально все авторы излагающие теорию относительности, свидетельствует о том, что величина ускорения хода времени на Земле, относительно времени на космическом корабле, не изотропна, то есть, зависит от направления ускорения, а, следовательно, не может быть связана с абсолютным замедлением хода времени на космическом корабле, вызываемым гравитационным полем, индуцированным всеми массами физической Вселенной.
7. Ускоренное движение
Рассчитать траекторию движения тела, которое движется с постоянным собственным ускорением в пространстве Минковского достаточно просто, особенно используя тригонометрические функции. Когда тело движется ускоренно в одном направлении с постоянным собственным ускорением a в течение собственного времени τ, ее мировая линия поворачивается на угол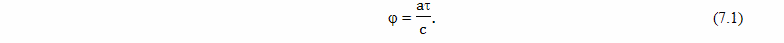
При этом, относительное замедление времени составит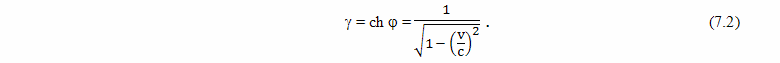
Поэтому, брату домоседу, наблюдающему за разгоном и производящему вычисления с помощью метода радарной одновременности, будет казаться, что, по мере роста скорости, космический корабль разгоняется все медленней и медленней. И в каждый конкретный момент времени, ускорение космического корабля с точки зрения наблюдателя с Земли равно величине a/γ.
Рассмотрим разгон космического корабля в системе отсчета наблюдателя с Земли. Каждому небольшому промежутку собственного времени прошедшему на космическом корабле dτ, будет соответствовать промежуток времени dt в системе отсчета наблюдателя с Земли. Эти промежутки времени связаны между собой соотношением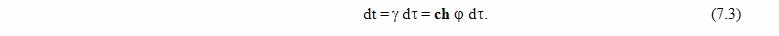
Найдем соотношение времени, прошедшего от момента старта на Земле и на космическом корабле: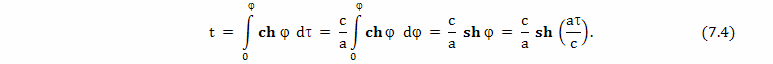
И, соответственно, из него следует обратное соотношение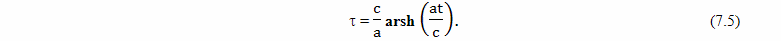
За малый промежуток времени dτ на космическом корабле, космический корабль пролетит расстояние в системе отсчета с Земли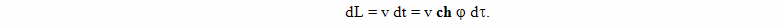
Делая подстановку v = c th φ, получаем соотношение: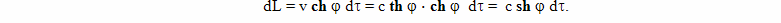
Следовательно, с момента старта от Земли, космический корабль преодолеет расстояние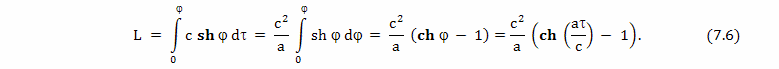
Можно выразить расстояние, пройденное космическим кораблем, стартовавшим от Земли, через время прошедшее у наблюдателя с Земли, для этого используем соотношение 7.4.
Из формул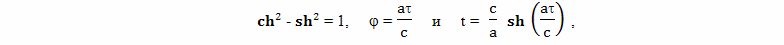
следует: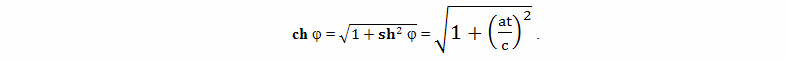
А, значит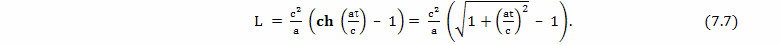
Теперь, используя выведенные формулы, можно точно рассчитать параметры ускоренного движения космического корабля, которые раньше в примере, рассмотренном в третьей главе, мы делали приближено.
Скорость 50 000 000 м/с в пространстве Минковского соответствует углу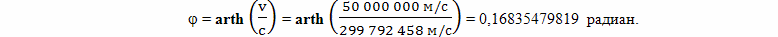
Для того, чтобы достичь такой скорости с заданным в примере собственным ускорением 100g=981м/с2, потребуется по часам ускоряющегося космонавта время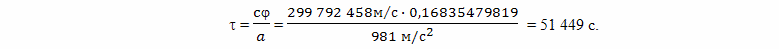
По часам наблюдателя оставшегося на Земле время ускоренного движения составит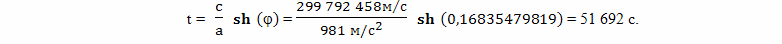
Приблизительный расчет по формулам классической физики для времени по часам наблюдателя с Земли дал время 50 968с. Ошибка в расчетах по приближенной методике составила 724 секунды или 1,4%. Эффект, связанный с относительным замедлением времени составит примерно 4 минуты.
Удаление от Земли в момент выключения двигателей составит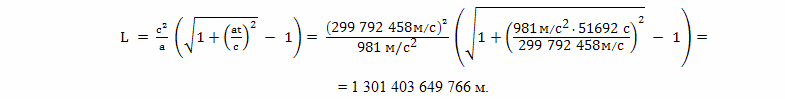
Расчет по формулам классической физики дал значение 1 275 090 162 138 метров, что на 2% меньше точной величины. Такая малая величина ошибки, при использовании формул классической физики для расчета ускоренного участка движения, объясняется тем, что скорость движения в рассмотренном примере сравнительно невелика, чуть меньше 0,2 от скорости света. По сравнению с разницей показаний часов братьев близнецов, составлявшей в рассмотренном примере величину порядка 20 месяцев, суммарной ошибкой в расчетах, равной 4·724 секунды можно пренебречь. И все выводы, сделанные на основании расчетов в прошлых главах, вполне обоснованы.
Если старт космического корабля происходит на некотором расстоянии L0 от инерциального наблюдателя и/или в момент старта t≠0 (по часам наблюдателя с Земли) или τ≠0 (по часам космонавта), космический корабль движется со скоростью v≠0 относительно инерциального наблюдателя, следует использовать более сложные формулы.
Вместо формулы (7.1), формулу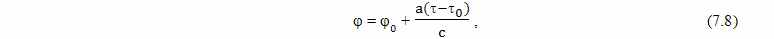
где: φ0 и φ - углы в пространстве Минковского между мировой линией инерциального наблюдателя на Земле и касательной к мировой линии ускоренно движущегося наблюдателя, соответственно в момент старта τ0 и в некоторый момент τ.
Вместо формулы (7.4), можно использовать формулу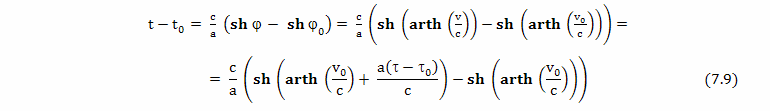
Вместо формулы (7.6), можно использовать формулу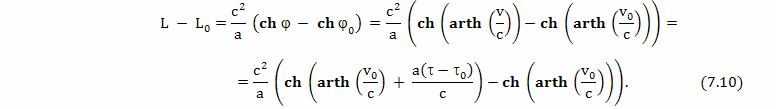
В формулах 7.0 и 7.10 величины v0 и v - скорость космического корабля относительно Земли соответственно, в моменты t0 и t, по часам наблюдателя с Земли или моменты τ0 и τ по часам космонавта; a - собственное ускорение космического корабля.
Теперь рассмотрим происходящее с точки зрения наблюдателя на космическом корабле, который, как и наблюдатель с Земли, использует метод радарной одновременности. Еще раз рассмотрим рисунок 13. Наблюдатель с Земли, измеряя расстояние L от Земли до космического корабля, считает одновременными события B и C, а наблюдатель, связанный с системой отсчета космического корабля, считает одновременными события D и C, поэтому и результат измерения расстояния между космическим кораблем и Землей L' у него будет другим. И для любого события C расстояние L' до события D будет в γ=ch φ раз меньше, чем расстояние L от события C до события B.
Из сказанного выше, легко вывести формулу расстояния от космического корабля до Земли в системе отсчета космического корабля, для космического корабля, стартовавшего в момент времени t0 по часам на Земле, или τ0 по часам космического корабля, от мировой линии наблюдателя на Земле, или просто любого другого инерциального наблюдателя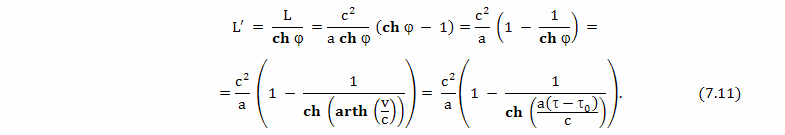
Космический корабль, начавший двигаться из точки с координатой L0≠0, соответственно, будет удаляться от Земли (в собственной системе отсчета) согласно формуле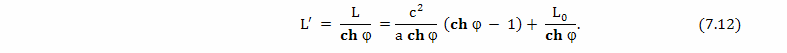
Особый случай, если космический корабль начинает движение из точки с координатой L0=c2/a, тогда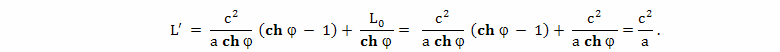
В этом случае, расстояние L' от космического корабля до Земли остается постоянной величиной на всем протяжении ускоренного полета. Если подставить величину L=c2/a в формулу (6.6), которая была рассмотрена в прошлой главе, то получится, что время на Земле остановилось относительно космического корабля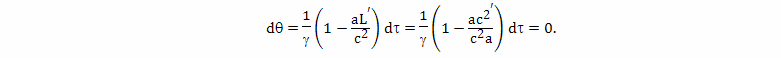
Причина такого явления заключается в том, что равноускоренный объект в пространстве Минковского движется по окружности радиусом R=c2/a. Имеется в виду, конечно же, постоянное собственное ускорение, направленное в одну сторону. И, если центр окружности расположен не в начале координат, а в некотором событии Q, то параметрическое уравнение движения объекта будет выглядеть так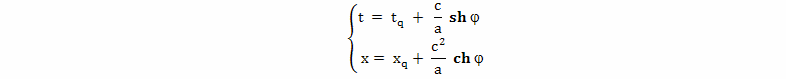
где: φ - параметр, зависящий от собственного времени τ на космическом корабле.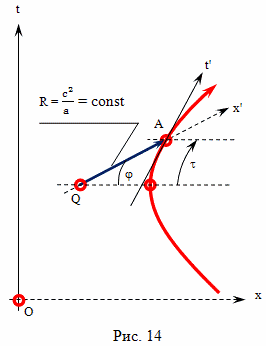
И, если получившаяся на диаграмме Минковского линия (рис. 14) мало похожа на привычную окружность, то причина в том, что это окружность, то есть, множество точек-событий, расположенных на одинаковом расстоянии от центра Q, именно в пространстве Минковского. А отображение этой окружности на евклидову плоскость (этот лист бумаги) действительно является гиперболой, а не окружностью. Свойства такой окружности в пространстве Минковского значительно отличаются от окружности в евклидовом пространстве. Какое пространство, такая и окружность.
По правилам определения интервала, то есть, расстояния между событиями в пространстве Минковского, определить, что расстояние от события Q до некоторой точки A, расположенной на окружности можно по формуле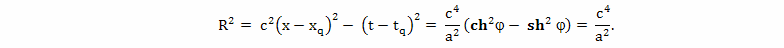
То есть,. 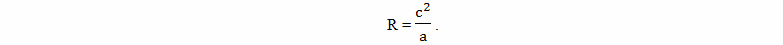
Предположим, что в точке-событии Q располагается Земля, тогда наблюдатель, находящийся на борту равноускоренно движущегося космического корабля, который использует метод радарной одновременности, в любой момент времени τ может построить прямоугольную декартову систему координат (t';x'), связанную со своей системой отсчета S' (рис. 14). И в любой момент времени на космическом корабле , которому соответствует событие A, он обнаружит, что ось координат t' является действительной прямой, касательной окружности в событии A. При этом перпендикулярная оси времени t' пространственная ось координат x' (перпендикулярная в пространстве Минковского, но не в его отображении на евклидову плоскость!) всегда будет пересекать точку-событие Q. Другими словами, в любой момент времени он обнаружит, что событие Q происходит одновременно с событием A в системе отсчета S'. Кроме этого, в любой момент времени он обнаружит, что расстояние от космического корабля до события Q равно величине R=c2/a. И, сколько бы времени космический корабль не двигался с постоянным собственным ускорением a, каждый раз проводя измерения и расчеты, этот наблюдатель обнаружит, что "сейчас" на Земле момент времени tq и расстояние до Земли равно все той же величине R.
Распространено заблуждение, согласно которому, ускорение космического корабля всегда вызывает относительное ускорение хода времени на Земле (или, относительное замедление хода времени на космическом корабле). Это не соответствует действительности, и рассмотренный выше пример наглядно демонстрирует это. В этом примере не только замедляется, но и вообще останавливается, время на Земле относительно космического корабля. Это заблуждение возникло только потому, что авторы трудов по теории относительности, описывающие парадокс близнецов, акцентируют свое внимание на определенном участке полета, когда на большом удалении от Земли космический корабль начинает ускоряться в направлении Земли.
Рассмотрим еще раз формулу (6.6). 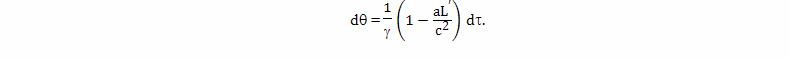
В зависимости от значений величин a и L, эта формула может описывать целый ряд вариантов, рассмотрение которых полезно для понимания парадокса близнецов.
Относительное ускорение хода времени на Земле (или, относительное замедление хода времени на космическом корабле), связанное с "потенциальным" членом, возникает только тогда, когда ускорение космического корабля направлено в сторону Земли. То есть, если величина aL<0. Геометрически это означает, что вектор расстояния от Земли до космического корабля и вектор ускорения направлены в противопроложные стороны. В этом случае, величина собственного ускорения a отрицательна, а, следовательно, величина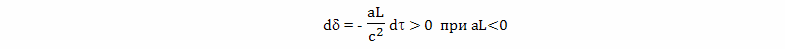
будет положительна и "потенциальный" член будет "ускорять" относительный ход времени на Земле. Это как раз тот случай, на котором обычно усиленно акцентируют внимание при доказательстве парадокса близнецов.
В случае если величина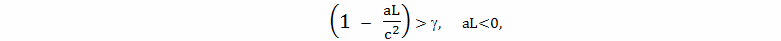
или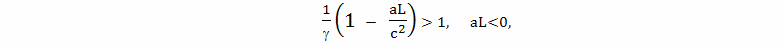
ход времени на Земле, относительно космического корабля будет ускоренным. Для этого достаточно того, чтобы абсолютное значение произведения aL было достаточно велико, то есть, должно выполняться условие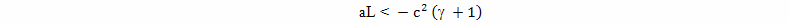
Второй случай, когдаособого интереса не представляет. При выполнении этого соотношения, ход времени на Земле, определенный путешественником по методу радарной одновременности, всегда будет замедленным. Но создать, на базе этого соотношения возражения против принятого Эйнштейном парадокса близнецов, не получится. Величина ускорения космического корабля, движение которого удовлетворяет этому условию, с удалением от Земли будет быстро уменьшаться, так быстро, что однажды стартовав с Земли, космический уже никогда не сможет вернуться. 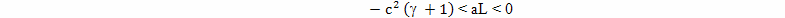
В случае, когда"потенциальный" член действует на замедление относительного хода времени на Земле, по отношению к космическому кораблю, совместно с пропорциональным членом. Когда мы рассматриваем большое космическое путешествие по сценарию парадокса близнецов, это условие выполняется, например, когда космический корабль в начале путешествия разгоняется к звезде или когда в конце путешествия тормозит. Но на этих участках величина L настолько мала, что эффектом относительного ускорения хода времени на космическом корабле относительно Земли в приближенных расчетах пренебрегают. 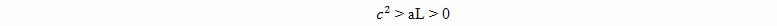
Случай, когда Мы уже рассмотрели немного выше (см. рис. 14). При этом 
следовательно, при любом значении dτ значение dθ = 0. То есть, ход времени на Земле относительно космического корабля, останавливается. И расстояние от космического корабля до Земли все время остается постоянным. 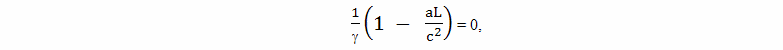
Еще более удивительными будут результаты измерений по методу радарной одновременности, если расстояние от ускоренно движущегося космического корабля до объекта Q превышает величину c2/a. В этом случае, "потенциальный" член оказывается меньше нуля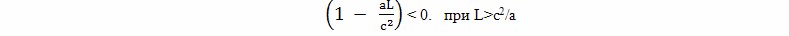
В результате, при небольшом увеличении собственного времени dτ, значение определенного расчетным путем одновременного момента θ объекта Q уменьшается (рис. 15).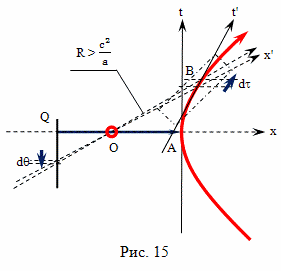
То есть, если объект Q это Земля, а такое может быть, если космический корабль стартует из точки удаленной от Земли на расстояние L>c2/a, то получается, что на Земле и на космическом корабле время идет в разные стороны.
Рассчитаем, на каком расстоянии от Земли должен происходить такой эксперимент для проверки данного явления. При a=100g, что было предположено в рассмотренных в прошлых главах примерах, расстояние от Земли до космического корабля должно превышать величину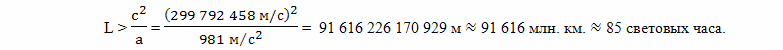
Это примерно в 637 раз больше, чем расстояние от Земли до Солнца и в 12,7 раз дальше от Солнца, чем Плутон. То есть, далеко за поясом Койпера. Если задать комфортное для космонавтов ускорение a=1g, то данное расстояние придется увеличить еще в 100 раз и получится почти световой год..
Если переместить космический корабль на немного большем расстоянии от Земли, остановить движение космического корабля относительно Земли, а, затем, начать ускоряться в противоположном от нее направлении, проводя измерения и расчеты по методу радарной одновременности, то наблюдатель на космическом корабле обнаружит, что расчетное одновременное ему событие сдвигается в прошлое. Результаты данного эксперимента можно трактовать двояко. Либо мы можем предположить, что время на космическом корабле пошло в обратном направлении относительно Земли, то ли, что на Земле время пошло в обратном направлении относительно Земли.
И, вот теперь, возникает вопрос, действительно ли в этом случае время на Земле и на космическом корабле идет в разные стороны, или это только эффект поворота системы отсчета, ничего общего с реальным ходом времени не имеющий. То есть, реально ли такое изменение направления времени или не реально?
На очень похожий вопрос в статье "Диалог по поводу возражений против теории относительности" Эйнштейн дает ответ
"На это я прежде всего должен заметить, что различать реальное и нереальное для нас не имеет смысла". [1, стр. 620]
И, далее:
"Вместо того чтобы различать реальное и нереальное, мы четко различаем величины, принадлежащие физической системе (независимо от выбора координатной системы), и величины, которые зависят от координатной системы. Далее следовало бы потребовать, чтобы физика вводила в свои законы лишь величины первого рода. На деле выяснилось, что этот путь практически нереален, как ясно показало развитие классической механики". [1, стр.621]
Здесь Эйнштейн, конечно, сильно преуменьшает возможности, которые дает полное принятие принципов относительности, но об этом поговорим в следующих главах.
Но в случае, когда мы рассматриваем относительное замедление времени, есть весьма резонный повод различать реальное и не реальное. Если в случае L>c2/a относительный ход времени в разных направлениях реален, то следует ожидать, что время на Земле, или время на космическом корабле должно пойти в другую сторону.
Но время на Земле и время на космическом корабле идут в разные стороны только с точки зрения ускоренно движущегося наблюдателя космического корабля, который использует для определения хода времени на Земле метод радарной одновременности. Наблюдатель с Земли, или любой другой инерциально движущийся наблюдатель, независимо от его положения в пространстве, значения и направления скорости, использующий такую же методику, определит, что время на космическом корабле идет в одном направлении, что и на Земле.
Так же дело обстоит и со случаем, когда L=c2/a. Если мы считаем, что относительный ход времени реален, то следует ожидать, что в результате маневров космического корабля ход времени на Земле действительно остановится, либо, что время на космическом корабле пойдет настолько быстро, что он мгновенно окажется в отдаленном будущем. И вновь, ни то ни другое не подтверждается наблюдениями ни из одной из инерциальных систем отсчета.
А, если в случаях L>c2/a и L=c2/a относительный ход времени в разных направлениях не является реальным, то есть, не связан с действительным направлением хода времени на Земле и на космическом корабле, то следует считать, что в случае aL<0 относительный ход времени тоже не является реальным. В таком случае, относительный ход времени и относительное ускорение/замедление времени одного из объектов относительно другого, никак нельзя связывать с действительными физическими процессами, происходящими на Земле и на космическом корабле.А, если так, то доказательство парадокса близнецов, приведенное Альбертом Эйнштейном, это просто хорошая иллюзия, и, рассматривая ход времени на космическом корабле относительно Земли, по методу радарной одновременности, никак нельзя судить об источнике абсолютной разницы во времени, возникающей на часах близнецов после завершения большого космического путешествия. И, на самом деле, доказательство Эйнштейна абсолютно ничего не доказывает, кроме того, что математический метод расчетов не содержит противоречий.
8. Эксперимент со свободно падающими часами
Принятое объяснение парадокса близнецов, в конечном итоге, строится на утверждении, что в ускоренной системе отсчета время идет иначе, не так, как в инерциальной системе отсчета. Ведь именно в "ускоряемой время от времени" системе отсчета, ход времени замедляется относительно хода времени инерциальной системы отсчета, связанной с наблюдателем на Земле. А наблюдатель на Земле, это инерциальная система отсчета, и с чего бы это ему менять ход времени? Инерциальная система отсчета это абсолют теории относительности. На основании данных, полученных по методу радарной одновременности для удаленных объектов, невозможно утверждать, что ход времени "там" реально замедляется или ускоряется именно на ускоренных участках полета. Но сравнение показаний часов при встрече близнецов до и после полета свидетельствует о том, что во "время от времени ускоряемой системе отсчета" объективно прошло меньше времени. И, возникает вопрос о том, где и когда было потеряно это время.
Оставшийся на Земле брат домосед в течение всего времени полета оставался в инерциальной системе отсчета. Если мы предполагаем реальное влияние на ход времени в этой системе маневров, которые совершает брат путешественник на космическом корабле, то должны предположить, также, влияние на ход времени на Земле значительного множества других ускоренно движущихся объектов по всей физической Вселенной. И, на их фоне, влияние на реальный ход времени на Земле ускоренно движущегося космического корабля окажется мизерным и, скорее всего слишком малым, чтобы быть обнаруженным.
Если мы предположим, что время объективно было потеряно при движении "туда" и "обратно", как в теории Лоренца, то, этим самым, мы признаем, что система отсчета наблюдателя на Земле, система отсчета путешественника при движении "туда", и система отсчета путешественника при движении "обратно", объективно имеют разные свойства. Но, различие между этими системами отсчета только в том, что они движутся относительно друг друга, и, следовательно, от скорости движения системы отсчета зависят ее физические свойства. Скорости движения относительно чего? И, так мы приходим к необходимости введения некой среды - эфира, взаимодействие с которым влияет на ход времени. Физики релятивисты ушли от подобных теорий еще в конце девятнадцатого века, и возвращаться к ним не намерены, о чем вполне ясно заявляли и Борн, и Планк.
Альтернативой является утверждение, что объективно время в разных инерциальных системах отсчета идет одинаково - все инерциальные системы отсчета физически равноправны. Вот, например, Я. П. Терлецкий в книге "Парадоксы теории относительности" вначале, в 11 параграфе, подробно описывает инерциальные системы отсчета и эффект относительного замедления времени, а, затем, в параграфе 12, переходя к рассмотрению ускоренных систем отсчета, пишет:
"Особенность этого кинематического следствия преобразований Лоренца состоит в том, что здесь отставание хода движущихся часов является вполне реальным эффектом, а не результатом избранной процедуры измерения, как это имело место в предыдущем параграфе". [12, стр. 43]
То есть, из этой цитаты видно, что Терлецкий утверждает, что наблюдаемое по методу радарной одновременности относительное замедление времени инерциально движущихся объектов, это только эффект, являющийся "результатом избранной процедуры измерения", а не реальным физическим явлением. Отмечу сразу, на этот счет существуют и другие мнения, которые я еще подробно рассмотрю в следующих главах.
Например, Эйнштейн пишет об относительном сокращении размеров:
"Вопрос о том, реально лоренцево сокращение или нет, не имеет смысла. Сокращение не является реальным, поскольку оно не существует для наблюдателя движущегося вместе с телом; однако оно реально, так как оно может быть принципиально доказано физическими средствами для наблюдателя, не движущегося вместе с телом". [1 стр. 187]
Точно так же, это высказывание можно отнести и к относительному замедлению времени движущегося объекта. В этом утверждении Эйнштейн не вполне корректен, поскольку он путает объективность явления (суть заданного вопроса) и объективноcть наблюдений, полученных по определенной методике. Это две совершенно разные вещи.
Когда измерительный инструмент движется относительно измеряемого тела, и мы используем классические методики измерения, то получаем не действительный размер тела, а проекцию этого размера на систему отсчета, к которой принадлежит измерительный инструмент. По той же причине, если мы принимаем, полностью и безоговорочно, эквивалентность всех инерциальных физических систем, то действительными физическими величинами движущегося объекта будет собственное время, собственные размеры, собственная масса, собственное ускорение и т.п., то есть, физические величины, которые измерены в системе отсчета этого тела.
Относительное замедление времени, Лоренцево сокращение размеров, и другие подобные явления, очень тесно связаны с самой процедурой измерения и интерпретацией результатов измерения. Например, ход времени движущегося тела можно измерять по несимметричному методу радарной одновременности, а можно по симметричному методу согласованной одновременности и эти методы, в большинстве случаев, дадут разные результаты.
Логика принципов относительности, принятых полностью и безо всяких оговорок, приводит к тому, что во всех инерциальных системах отсчета время идет одинаково, независимо от их относительных скоростей движения - ведь все они физически эквивалентны. И, тогда, остается только предположить, что абсолютная разница в ходе часов брата домоседа и брата путешественника образовалась на ускоренном участке полета.
Но, подобное утверждение полностью опровергается мысленным экспериментом с падающими часами. Давайте предположим, что брат путешественник кроме наблюдений за далекой Землей проводит еще некоторые другие физические эксперименты с часами. Например, можно сравнить ход часов закрепленных на космическом корабле и часов, свободно падающих в кабине космического корабля или рядом с ним.
В рассмотренном в предыдущей главе примере, собственное время движения на одном ускоренном участке составило 51 449 секунд, а таких участков за время путешествия всего четыре. Таким образом, общее собственное время движения с ускорением составило 205 796 секунд. Из расчетов, проведенных в пятой главе, следует, что абсолютная разница во времени между часами брата путешественника и брата домоседа составила 13 908 125 секунд. То есть, для того чтобы объяснить образовавшуюся разницу именно физическими эффектами возникающими при ускоренном движении, нужно предположить, что на участках ускоренного движения часы на космическом корабле шли в среднем в 67,58 раз медленнее, чем на Земле. Учитывая, что относительное замедление времени на инерциальных участках полета не превышало величины γmax = 1,014205177, не заметить такое физическое явление трудно.
Если это явление проявляется как замедление хода времени на космическом корабле, то обнаружить его очень просто. Достаточно космонавту в ускоренно движущемся космическом корабле проделать следующий эксперимент. Вначале синхронизировать три хронометра, один хронометр закрепить в задней части космического корабля, второй закрепить в передней части корабля, а третий просто отпустить, так, чтобы он, под действием ускорения космического корабля начал смещаться от передней части к задней части. Теперь, методом фотофиниша можно определить время, прошедшее на падающих часах, с большой точностью.
В тот момент, когда космонавт перестает держать хронометр в руке, этот хронометр перестает быть ускоренной системой отсчета и становится объектом, который движется прямолинейно и равномерно, относительно наблюдателя на Земле. Если ход времени на космическом корабле при ускоренном движении действительно замедляется, то в данном эксперименте космонавт будет наблюдать, что свободно падающие часы идут примерно в 67,58 раз быстрее, чем часы, ускоренные вместе с космонавтом. Но такого быть не может, сразу по нескольким причинам.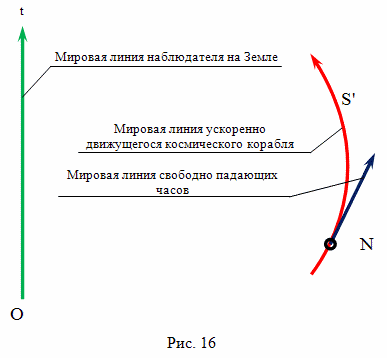
Во-первых, такое видимое замедление хода падающих часов должно прямо пропорционально зависеть от расстояния, на котором расположен инерциальный наблюдатель. И, если этот наблюдатель расположен в соседней галактике, то часы пойдут в миллионы раз быстрее, а если совсем недалеко, то почти так же, как и ускоренные часы. А если за процессом наблюдают сразу несколько существ с разных расстояний? И как вообще сам процесс наблюдения может повлиять на ход времени удаленного объекта?
Во-вторых, представьте себе игру в пинг-понг при ТАКОЙ физике. Пока вы бьете по шарику, он имеет нормальную скорость течения времени, а когда он отрывается от ракетки, ход времени меняется, и, вместе с ним, скачкообразно в десятки раз меняется масса, энергия и импульс шарика. Это не классическая физика и точно не физика теории относительности.
В-третьих, необходимо учитывать принцип однородности свойств физической вселенной. Согласно этому принципу, все физические процессы происходят одинаково, в любой области вселенной, с учетом, конечно, местных особенностей, таких как гравитационные поля и т.п. Но, в рассматриваемом случае, таких особенностей не предусмотрено, ни сильных гравитационных полей (поле создаваемое Землей и Солнцем недостаточно, чтобы оказать значительное действие), ни других существенных особенностей. Из этого принципа следует, что физические эффекты, связанные с ускоренным движением, можно наблюдать, вовсе не удаляясь от Земли, ведь всегда можно представить себе, что в далеких звездных системах есть жизнь и потенциальные наблюдатели. Но ускоренное движение не оказывает ТАКОГО влияния на ход времени в наблюдаемых условиях. Из этого можно сделать вывод, что и в удаленных от Земли ускоренных системах отсчета ТАКОГО влияния на ход времени не происходит.
Альберт Эйнштейн не случайно пишет в своих статьях о том, что ускоренное движение космического корабля, ускоряющегося в направлении Земли, вызывает относительное ускорение хода времени на Земле и ничего не пишет о замедлении хода времени на космическом корабле. Ускоренное движение космического корабля никак не влияет на абсолютный ход времени на самом космическом корабле и Эйнштейн это знал, иначе бы он не стал настолько усложнять логику этого процесса в теории относительности.
Рассмотрим еще один мысленный эксперимент. Пусть, вдали от Земли ускоренно движутся два космических корабля. Один из них (S') ускоряется в направлении Земли, а другой (S'') в противоположном направлении (рис. 17).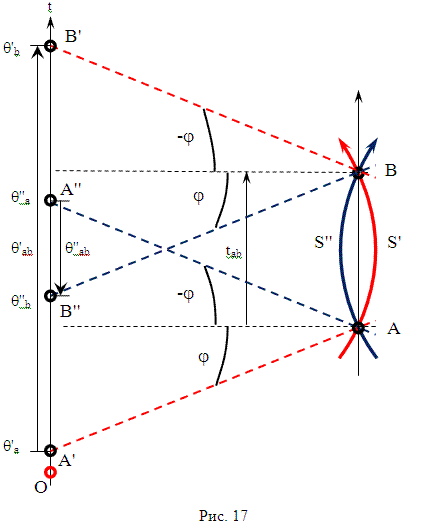
Примем следующее. Абсолютные величины собственных ускорений обоих объектов S' и S'' равны и ускорения направлены в противоположные направления. Величины ускорений всегда могут быть измерены относительно инерциальной системы отсчета и, поэтому, являются абсолютными значениями. Поэтому, мы всегда можем точно утверждать, в каком направлении ориентировано ускорение, и мы всегда можем утверждать, что два этих значения равны по абсолютной величине друг другу или одно больше другого, независимо от их направления в пространстве. Эти данные инвариантны, то есть, они никак не будут зависеть от выбора инерциальной или даже ускоренной системы отсчета.
В двух событиях A и B, равноудаленных от Земли, и лежащих в одной пространственно-временной плоскости, образованными действительной прямой Ot и перпендикулярной ей мнимой прямой Ox, объекты сближаются между собой. В событии A скорость объекта S' равна величине v относительно Земли, а скорость объекта S'' относительно Земли равна величине -v. В событии B скорость объекта S' равна величине -v относительно Земли, а скорость объекта S'' относительно Земли равна величине v. Расстояние между событиями A и B в пространстве Минковского, то есть, интервал времени по прямой мировой линии, соединяющей эти события, равно некоторой величине tab.
Собственное время объекта S', прошедшее между событиями A и B, можно рассчитать по формуле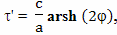
в которой
Собственное время объекта S'', прошедшее между событиями A и B, можно рассчитать по формуле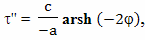
в которой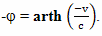
Легко убедится, что по часам обоих ускоренных объектов между событиями A и B прошло одинаковое время. И, было бы странно, если бы результат оказался иным. Прямая действительная линия, соединяющая события A и B, является осью симметрии мировых линий объектов S' и S''. Равенство собственного времени, прошедшего по часам этих объектов между событиями A и B, следует из принципов однородности и изотропности пространства.
Наблюдатели S' и S'' в событиях A и B по методу радарной одновременности определяют одновременный им момент времени на Земле. Наблюдатель S' определит, что одновременно с событием A на Земле произошло событие A', а одновременно с событием B на Земле произошло событие B'. Соответственно, наблюдатель S'' определит, что одновременно с событием A на Земле произошло событие A'', а одновременно с событием B на Земле произошло событие B''. И, каждый из них определит в своей системе отсчета, что расстояние до Земли в этих событиях равно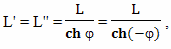
где: L - расстояние от Земли до событий A и B, в системе отсчета наблюдателя с Земли, L' и L'' - расстояние от Земли до событий A и B в системах отсчета S' и S''.
И теперь, по результатам измерений в системе отсчета S', за собственное время на космическом корабле τ', между событиями A и B, на Земле прошло время равное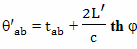
В то же время, по результатам измерений в системе отсчета S'', за собственное время на космическом корабле ', между событиями A и B, на Земле прошло время равное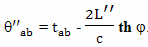
При достаточно большом значении L'' значение θ''ab будет отрицательным числом, как это показано на рисунке 17.
Мы выяснили, что в ускоренных системах отсчета S' и S'' между событиями A и B прошло по их часам одинаковое время. И, если предположить, основываясь на наблюдениях по методу радарной одновременности в системе отсчета S', что на Земле действительно прошло время θ'ab, то необходимо признать и то, что на Земле действительно прошло время θ''ab. Более того, необходимо признать, что, возможно, время на Земле шло одновременно в разные стороны, основываясь на наблюдениях в системах отсчета S' и S''. И, если основываться на принципах философского релятивизма, точнее, эмпириокритицизма, одним из авторов которого был Эрнст Мах, то ничего необычного в этом нет.
Действительно, если считать, что объективной физической реальности не существует, и у каждого субъекта есть своя индивидуальная физическая реальность, то вполне понятно, что в субъективной вселенной наблюдателя S' на Земле прошло время θ'ab, а в субъективной вселенной наблюдателя S'' на Земле прошло время θ''ab. И спрашивать о том, какое же время в действительности прошло на Земле, нет смысла, потому что, с точки зрения философского релятивизма, объективной реальности вообще не существует.
И, тогда, события в разных физических реальностях могут происходить действительно в разных последовательностях (и не только потому, что удалены друг от друга в пространстве), и, даже, могут происходить совершенно разные события. В одной из физических реальностей, кот в закрытом помещении в определенный момент времени будет жив, в другой физической реальности этот же кот, в этот же момент времени, будет мертв. А в третьей реальности в этом помещении в этот момент времени вообще не будет кота, а в четвертой субъективной физической реальности в этом закрытом помещении будет сразу несколько разных котов и кошек.
Вот, только, при таком подходе к реальности, право на свою собственную субъективную реальность должны получить не только разумные существа - наблюдатели, но и любые другие материальные объекты, и, даже системы отсчета не привязанные к какому-то объекту. И, тогда, стирается само понятие "субъект", поскольку "не субъектов" во Вселенной просто не остается.
Но сам Альберт Эйнштейн, и ряд других ведущих физиков релятивистов, неоднократно выступали с заявлениями о том, что теория относительности Эйнштейна не имеет никакого отношения к философскому релятивизму, и физическая реальность этой Вселенной существует объективно. В теории относительности Эйнштейна мы не всегда можем определить последовательность нескольких событий только потому, что световые сигналы от них к разным наблюдателям приходят в разной последовательности, но последовательность событий, расположенные относительно друг друга в относительном прошлом и в относительном будущем одинакова для всех наблюдателей и все события происходят объективно.
Используя метод радарной одновременности, наблюдатель S' определит, что, между событиями A и B, на Земле прошло время θ', а наблюдатель S'' определит, что на Земле прошло время θ''. Но нельзя утверждать, что для наблюдателя на Земле действительно прошло и время θ', и время θ''. Как, нельзя и отдать предпочтение одному из них. Если мы руководствуемся фундаментальным принципом, гласящим, что физическая реальность объективна, то интервалам собственного времени τ' и τ'', прошедшему по часам объектов S' и S'' между событиями A и B, должно соответствовать вполне определенное время t, прошедшее на Земле, а не два разных промежутка времени. Другое дело, что, как часто утверждают в источниках по теории относительности, у нас нет средств, позволяющих объективно измерить ход времени удаленных объектов. И, на этом основании делается вывод, что, раз у нас нет средств, позволяющих объективно соотнести ход времени удаленных объектов, то нет и смысла задавать вопрос о том, какое время в действительности прошло на Земле.
Утверждение спорное, потому, что если мы утверждаем полную физическую эквивалентность всех инерциальных систем отсчета, то должны признать и то, что ход времени в них объективно одинаков. Правда, в рассматриваемом на рисунке 16 случае, мы сравниваем ход времени в инерциальной системе отсчета Земли S с ходом времени в ускоренных системах отсчета S' и S''. А, ведь, Альберт Эйнштейн утверждал, что физически эквивалентны только инерциальные системы отсчета, а в ускоренных системах отсчета физические процессы протекают не так, как системах инерциальных. Это правда, многие физические процессы в ускоренных системах отсчета протекают иначе, но, когда мы исследуем парадокс близнецов, нас вовсе не интересуют все физические процессы. Нас интересует только ход времени в самой физической системе.
Вернемся к эксперименту со свободно падающими часами в кабине космического корабля. Когда брат путешественник, измеряет по методу радарной одновременности ход времени на удаленной от него Земле, он не может получить объективный результат, который бы позволил определить действительный ход времени на Земле. А, значит, и не нужно использовать этот метод, который в принципе не может дать интересующие нас данные. Но брат путешественник может руководствоваться провозглашенным Альбертом Эйнштейном принципом полной физической эквивалентности инерциальных систем. Кроме того, на ускоренных участках полета, он может производить эксперименты со свободно падающими часами, которые могут побудить его сформулировать следующий частный принцип относительности в отношении хода времени:
Время в любой ускорений физической системе идет точно так же, как в инерциальной системе, находящейся в данный момент времени в той же точке пространства, и движущейся в том же направлении, и с той же скоростью.
Этого вполне достаточно, чтобы сформулировать парадокс близнецов еще в одной редакции:
Все время полета брата близнеца, он был либо в инерциальной системе отсчета, когда двигался равномерно и прямолинейно, и время у него, согласно принципам относительности, должно было идти точно так же, как и на Земле. Либо, когда он двигался ускоренно, то время у него шло точно так же, как и в инерциальной системе отсчета, находящейся в тот же момент времени и в той же точке пространства, и движущейся в том же направлении и с той же скоростью.
Если признать, что все инерциальные системы отсчета физически эквивалентны, то это означает, что в любой момент времени путешествия, время на космическом корабле должно идти точно так же, как и на Земле. Но тогда, почему при возвращении на Землю оказывается, что у брата путешественника прошло больше времени, чем у брата, оставшегося на Земле?
У данной редакции парадокса есть, по крайней мере, два принципиально разных объяснения, но оба они требуют изменений современных представлений о теории относительности Альберта Эйнштейна.
9. Полет по змейке
Обычный сценарий большого космического путешествия, описанного в парадоксе близнецов очень прост: прилетел, увидел и полетел обратно. Но можно немного усложнить такой сценарий. Предположим, что в наиболее удаленной от Земли точке, путешественник проводит исследования и для этого ему приходится многократно ускоряться в направлении Земли и в обратном направлении (рис. 18). Назовем такой маршрут движения "полет по змейке".
Расчет такого полета будем вести по всем правилам, по точным формулам, рассмотренным в прошлой главе, вначале в системе отсчета наблюдателя с Земли, затем, в системе отсчета брата путешественника и сравним полученные результаты. За основу возьмем пример из 3 главы. То есть, предположим, что цель путешествия расположена на расстоянии L = 5·1016 м, большую часть времени космический корабль движется со скоростью v = 50 000 000 м/с, а на участках разгона и торможения величина ускорения составляет 100g.
Вначале, маневрирование в районе цели путешествия не будем учитывать, и рассчитаем только участки полета "туда" и "обратно". Начнем с того, у нас есть четыре подобных участка равноускоренного полета, то есть, полета с постоянным собственным ускорением a=981м/с2, на которых скорость движения космического корабля меняется на величину v = 50 000 000 м/с. При этом, мировая линия поворачивается на угол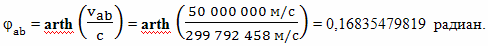
И для этого требуется собственное время на космическом корабле, равное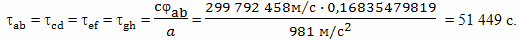
В системе отсчета наблюдателя с Земли, все эти четыре участка имеют продолжительность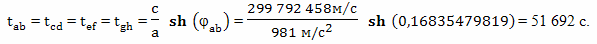
Космический корабль, при этом, с точки зрения наблюдателя с Земли, на каждом из четырех участков, преодолевает расстояние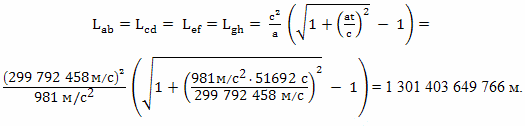
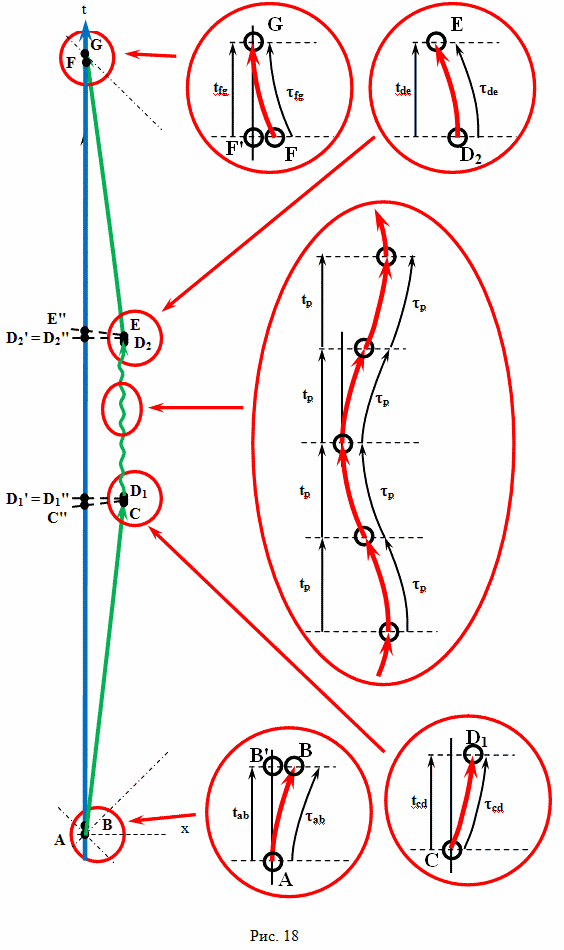
Остальное расстояние космический корабль преодолевает, двигаясь равномерно и прямолинейно. По часам наблюдателя с Земли, на это потребуется время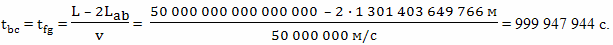
По часам на космическом корабле, на это потребуется время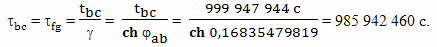
Суммируем время отдельных участков полета в одну сторону в системе отсчета наблюдателя с Земли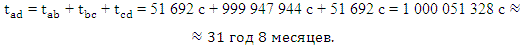
Суммируем время отдельных участков полета в одну сторону по часам наблюдателя на космическом корабле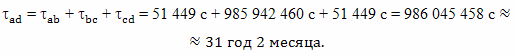
После простого полета "туда" и "обратно" разница показаний часов брата оставшегося на Земле и брата путешественника составит 14 005 870 секунд, это примерно 162 дня. Практически такие же результаты мы получили во второй главе, рассчитывая большое космическое путешествие по приближенной методике. Рассмотрим отдельно, удаленный от Земли участок ускоренного движения такого "простого" путешествия (рис. 19). В событии C брат путешественник, используя метод радарной одновременности, определит, что одновременным ему на Земле является событие C', в событии D, соответственно, D' и в событии E одновременным он признает событие E'.
С точки зрения наблюдателя с Земли события C и D удалены на расстояние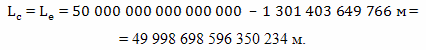
Но, согласно расчетам брата путешественника, в событиях C и D Земля удалена от него на расстояние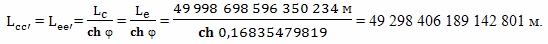
В событии D скорость путешественника относительно Земли равна нулю и при определении расстояния между ними разногласий не возникнет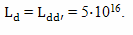
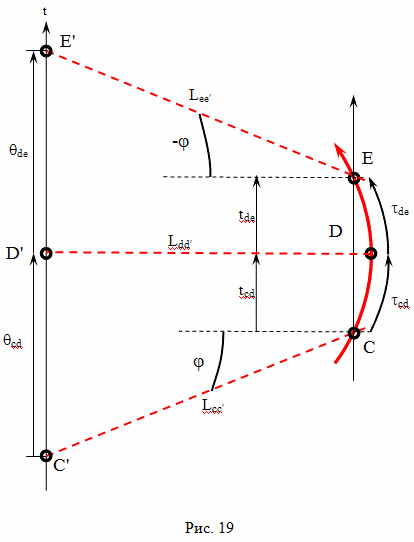
И, пользуясь методом радарной одновременности, путешественник рассчитает, что между событиями C' и D' на Земле прошло время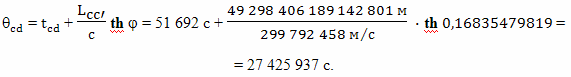
То есть, в среднем, время на Земле, согласно этим расчетам шло в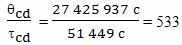
раза быстрее, чем на космическом корабле.
И, согласно этим же расчетам, с точки зрения путешественника, за это время Земля удалилась от космического корабля на расстояние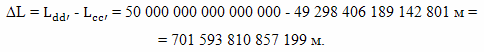
Средняя скорость удаления Земли относительно космического корабля составила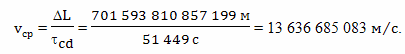
Это примерно в 45 раз быстрее скорости света.
Следует понимать, что определенное по методу радарной одновременности время на Земле и расстояние от космического корабля до Земли, в системе отсчета путешественника, это не два разных измерения, это неотъемлемые части одного измерения.
То есть, в событии C путешественник определяет, что Земля находится в точке C' и до нее расстояние Lcc', а в событии D он определяет, что Земля находится в точке D' и до нее расстояние Ldd'. Если изменится положение Земли в пространстве Минковского, изменится и расстояние до нее, и, наоборот. Эти данные жестко связаны между собой. И, если мы считаем достоверным одно из данных измерения, то должны считать достоверным и другое. Если мы считаем одно из них недостоверным, то не можем считать достоверным другое.
И, если мы считаем, что время на Земле действительно шло в 533 раза быстрее, чем на космическом корабле, то мы должны признать, что Земля относительно космического корабля действительно двигалась со скоростью в 45 раз больше скорости света, что масса Земли в этот промежуток времени действительно была мнимой величиной, и тому подобное.
Если мы считаем, что Земля в действительности не могла двигаться быстрее скорости света в 45 раз, то обязаны признать недостоверными и данные о том, что время на Земле действительно шло в 533 раз быстрее, чем на космическом корабле. А, следовательно, относительный ход времени, рассчитанный по методу радарной одновременности, не имеет прямого отношения к действительному ходу времени на Земле. И, использовать эту величину для объяснения парадокса близнецов некорректно.
Относительный ход времени, определенный при помощи метода радарной одновременности, напрямую не связан с реальным ходом времени на Земле и космическом корабле. При помощи этого метода определить источник появления абсолютной разницы в показаниях часов братьев близнецов, когда они их сверяют во время встречи, невозможно. В статье Эйнштейна "Диалог по поводу возражений против теории относительности" приводится еще предположение, что источником этой разницы является наличие ускоренных участков полета космического корабля. И, чаще всего, это высказывание трактуется буквально, что именно на ускоренных участках полета происходит появление абсолютной разницы в показаниях часов. И, что на ускоренных участках полета замедляется ход времени на космическом корабле.
Так это, или нет, можно определить, анализируя "полет по змейке". Если верно данное предположение, то увеличив в разы время ускоренного движения космического корабля, мы должны получить увеличение разницы между показаниями часов братьев близнецов тоже в разы. Проверим это.
Пусть, между событиями D1 и D2 путешественник постоянно ускорялся в направлении Земли, а, затем, в обратную сторону. Для определенности, будем считать, что на этом промежутке космический корабль сделал 9 полных циклов разгона. Вначале он разгонялся в направлении к Земле до скорости -v, тормозил, разгонялся в обратную сторону до скорости +v, опять тормозил, и возвращался к цели путешествия. Затем, все это повторялось.
При этом общее время движения с ускорением, за все время путешествия, возрастет ровно в 10 раз, с точки зрения путешественника, и ровно в 10 раз, с точки зрения наблюдателя на Земле. И, с точки зрения обоих наблюдателей, общее время движения с некоторой скоростью относительно Земли, возрастет не в разы, а в число раз, выраженное единицей и какими-то цифрами после запятой.
Если ускоренное движение космического корабля замедляет ход времени на нем, и именно этим объясняется абсолютная разница возникшая в конце путешествия, то следует ожидать, что эффект появления абсолютной разницы между показаниями часов братьев близнецов будет пропорционален времени действия причины его вызвавшей. И, такое замедляющее действие гравитационного поля не должно зависеть от направления ускорения.
Таким образом, если абсолютная разница возникает на ускоренных участках, то и абсолютная разница в показаниях часов братьев, после завершения путешествия, должна вырасти в разы. Если абсолютная разница возникает за счет разности скоростей между путешественником и Землей, то прирост абсолютной разницы в показаниях часов должен увеличиться не в разы, а в число, несколько превышающее единицу.
С точки зрения наблюдателя с Земли, каждый из девяти полных циклов разгон - торможение - разгон - торможение идентичен одному участку разгона от события A до события B. Получаем девять полных циклов, в каждом из которых, четыре идентичных участка. Поэтому, все маневры космического корабля, с точки зрения наблюдателя на Земле, займут время, равное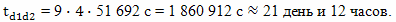
А, по часам космического корабля между событиями D1 и D2 пройдет время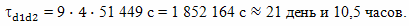
Общее время путешествия увеличится, по часам брата оставшегося на Земле, до величины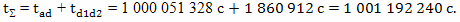
И, общее время путешествия увеличится, по часам брата путешественника, до величины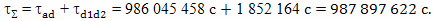
Теперь, разница между показаниями часов братьев близнецов будет составлять 14 014 618 секунд.
То, есть, при "пролете змейкой" разница между показаниями часов братьев близнецов увеличивается на величину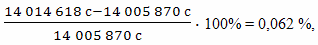
или в 1,00062 раза.
Расчет показывает, что источником абсолютной разницы между показаниями часов братьев близнецов эффект замедления времени на космическом корабле, при его ускоренном движении, быть не может. Но эта величина хорошо соответствует предположению о том, что разница образовалась только за счет движения с разными скоростями, как это было в теории Лоренца.
Еще раз предположим, что абсолютная разность показаний часов образовалась за счет ускорения хода времени на Земле, при ускоренном движении космического корабля. Рассчитаем и этот вариант.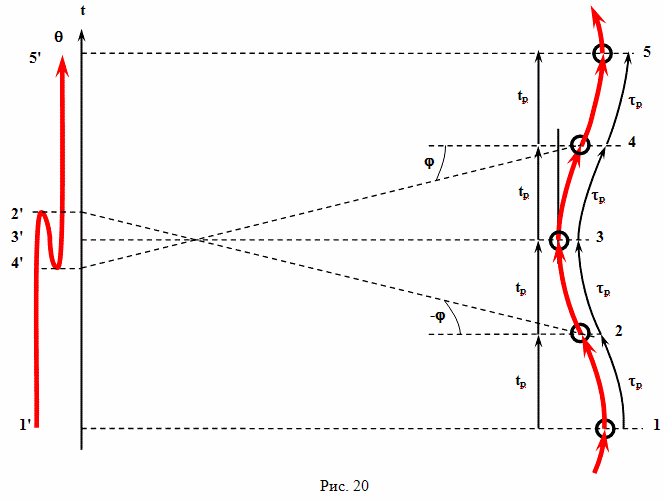
Каждый из девяти составляющих "полет по змейке" циклов выглядит так, как это показано на схеме на рисунке 20. В каждом из циклов космический корабль вначале разгоняется в направлении Земли (участок 1-2), затем уменьшает свою скорость относительно Земли (участок 2-3), ускоряется в направлении противоположном Земле (участок 3-4), и, затем, снова уменьшает свою скорость относительно Земли (участок 4-5). Космический корабль ускоряется на всех участках с одинаковым постоянным собственным ускорением a, поэтому, время прохождения каждого из участков одинаково, как в системе координат наблюдателя Земли (tр), так и наблюдателя на космическом корабле (τр). В следующем цикле все повторяется точно так же.
Рассчитывая по методу радарной одновременности одновременное ему время на Земле, путешественник сопоставит событию 1 событие 1', событию 2 событие 2', и так далее. Согласно этим расчетам, пока на участке 1-2 космический корабль ускорялся в направлении Земли, на Земле прошло время 12, большее, чем время на космическом корабле τ12 = τр. Затем, направление ускорения меняется и на участке 2-3-4 путешественник "наблюдает" что время на Земле идет в обратном направлении.
Слово "наблюдает" взято в кавычки, потому что непосредственно наблюдениями обратный ход времени на Земле не подтверждается. Вывод о том, что время на Земле шло в обратном направлении, сделан на основе расчетов по методу радарной одновременности. Сама Земля в это время удалена от космического корабля и электромагнитное излучение от нее будет идти значительное время. Но и позднее, когда свет, излученный на Земле в период между событиями D1' и D2', все же, достигнет космического корабля, космонавт тоже не будет наблюдать поворота времени на Земле вспять.
Но, если предположить, что Земля все же, действительно движется во времени, перемещаясь, то в одном направлении, то в другом, в зависимости от направления ускорения космического корабля, расчеты сходятся с тем результатом, который необходимо получить.
По этим расчетам, между событиями 1 и 2 на космическом корабле, на Земле пройдет время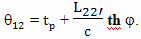
Между событиями 2 и 3 на космическом корабле, на Земле пройдет время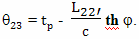
Между событиями 3 и 4 на космическом корабле, на Земле пройдет время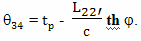
И, между событиями 4 и 5 на космическом корабле, на Земле пройдет время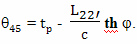
Суммируя, получим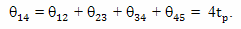
И, сколько бы таких циклов ни было, продолжительность каждого цикла по часам расположенным на Земле, и с точки зрения наблюдателя с Земли, и с точки зрения наблюдателя космического корабля, совпадет.
Таким образом, как и в предыдущем расчете, мы получим, что собственному времени на космическом корабле между событиями D1 и D2, равному 1 852 164 с, будет соответствовать время 1 860 912 с по часам расположенным на Земле.
В этом варианте, расчеты дают необходимый результат, но предположение о том, что разница показаний часов братьев близнецов образуется на ускоренных участках полета, неизбежно приводит к выводу, что в результате ускоренного движения космического корабля изменялся ход времени именно на Земле, а не на космическом корабле. Причем, если мы считаем, что ДЕЙСТВИТЕЛЬНО изменялся ход времени на Земле, то мы должны признать и то, что в случае "полета змейкой" ДЕЙСТВИТЕЛЬНО время на Земле иногда шло в обратном направлении. Иначе правильного результата расчетов не получить.
10. Релятивистский эффект Доплера
Большую часть полета, находясь на значительном расстоянии от Земли, брат путешественник может наблюдать события на Земле с большим опозданием, как раз на то время, в течение которого электромагнитное излучение от Земли достигнет космического корабля. И этот интервал времени может измеряться в годах. И, именно удаленность событий, является одной из причин невозможности абсолютного определения пар одновременных событий на космическом корабле и на Земле.
Находящийся на удалении от Земли брат путешественник может наблюдать только приходящие к нему электромагнитные сигналы, и, используя их, измерять видимое расстояние от космического корабля до некоторых объектов, измерять скорость космического корабля относительно некоторых объектов, и получать сигналы точного времени с Земли или других объектов. Но, сигналы точного времени, полученные в некоторый момент на космическом корабле, были испущены значительное время назад. Определить же, какое время на Земле сейчас, можно только при помощи расчетов, предварительно задав систему отсчета, в которой будет исчисляться одновременность событий.
Для начала выясним, как будет изменяться частота сигнала, испущенного на Земле. Рассмотрим космический корабль, который первоначально (t0=0, φ0=0 и τ0=0) находится на расстоянии R от начала координат, и начинает с постоянным собственным ускорением a=c2/R ускоряться в противоположную от начала координат сторону (рис. 21).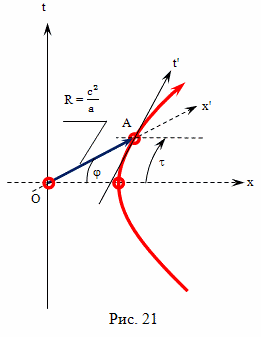
Движение этого космического корабля будет описываться уравнением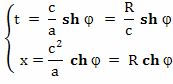
где: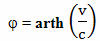
параметр, зависящий от скорости движения космического корабля. Кроме того, этот параметр является функцией собственного времени ускоренно движущегося космического корабля и величины постоянного собственного ускорения a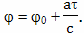
Где: φ - угол между касательной к мировой линии, φ0 - угол между касательной к мировой линии в начальный момент времени, a - величина собственного ускорения, τ - собственное время, прошедшее с начального момента времени, c - скорость света.
А теперь, посмотрим, как будет меняться частота сигнала, передаваемого источником, неподвижным в выбранной системе координат, с точки зрения наблюдателя на космическом корабле (рис. 22). Пусть период передаваемого сигнала составит небольшой промежуток времени dT0. Причем, не столь важно, передан этот сигнал из системы отсчета находящейся в начале координат, или в любой другой системы отсчета t'', неподвижной относительно нее и находящейся в том же направлении от космического корабля, что и начало отсчета.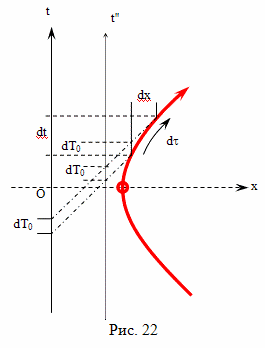
Очевидно, если космический корабль удаляется от источника сигнала, то сигналу, испущенному позже, придется пройти дополнительное расстояние dx и этот сигнал достигнет цели на время dt позже. Сигнал движется со скоростью света, поэтому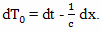
В случае, когда космический корабль приближается к источнику сигналов, сигналу, испущенному позже, придется пройти меньшее расстояние, но эта разница в формулу войдет как отрицательное число, и написанная выше формула тоже будет верна.
Следовательно: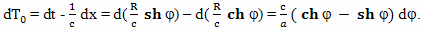
. Подставляем тождества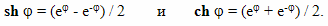
И получаем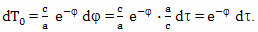
Соответственно, если излучаемый на Земле сигнал имеет период T0, то принимаемый на на ускоренно движущемся космическом корабле сигнал будет иметь период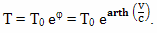
Если испускаемый сигнал имеет частоту f0, то наблюдатель на ускоренно движущемся космическом корабле примет сигнал с частотой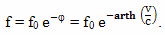
В источниках по теории относительности можно найти аналогичные формулы для объектов движущихся неускоренно. Например, в книге В. А. Угарова "Специальная теория относительности" [5, стр. 250] дан вывод соотношений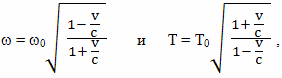
где: ω = 2πf и ω0 = 2πf0 - соответственно, циклические частоты принятого и испущенного сигналов. Это эффект Доплера, для случая, когда относительная скорость приемника и передатчика сигнала сравнима со скоростью света.
Подставив в эти формулы соотношение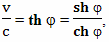
получим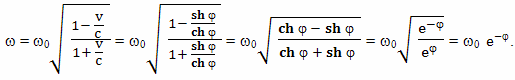
И, аналогично: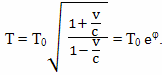
Эти формулы тождественны формулам, выведенным выше для ускоренно движущегося объекта. Из этого можно в очередной раз сделать вывод. Зависимость частот принимаемого и переданного сигналов это чистый эффект Доплера. Фактор ускорения никак не влияет частоту принимаемого сигнала, а, следовательно, никак не влияет на ход времени в физической системе.
И, эти формулы означают еще и то, что путешественник, непосредственно наблюдая за ходом времени на Земле, отметит эффект Доплера в его релятивистском варианте, и только. Никакого видимого хода времени "туда и обратно" связанного именно с ускорением, он не должен отметить. Рассмотрим частоту f принимаемого на космическом корабле сигнала с Земли, как функцию собственного времени космического корабля (рис. 23).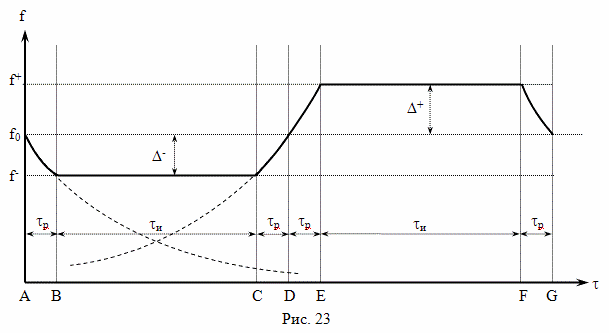
Вначале, в событии A, частота принимаемого на космическом корабле сигнала равна частоте передаваемого сигнала с Земли f0. Затем, по мере разгона космическо корабля с постоянным собственным ускорением, на участке AB, частота принимаемого сигнала убывает по экспоненте. На участке между событиями B и C, когда космический корабль движется равномерно и прямолинейно удаляясь от Земли, частота принимаемого сигнала f- остается постоянной. Затем, между событиями C и E частота принимаемого сигнала по экспоненте увеличивается. В событии D скорость космического корабля относительно Земли равна нулю и частота принимаемого сигнала совпадает с частотой сигнала передаваемого с Земли. Между событиями E и F космический корабль движется равномерно и прямолинейно приближаясь к Земли, и частота принимаемого сигнала f+ остается постоянной. На заключительном участке полета, между событиями F и G космический корабль снижает свою скорость относительно Земли с постоянным собственным ускорением и частота сигнала снижается по экспоненте, достигая значения f0 в событии G. Это именно то, что реально во время полета к звезде наблюдает брат путешественник.
Поскольку мы считаем, что космический корабль все время ускорялся с постоянным собственным ускорением a, что время τр каждого из участков ускоренного движения одинаково, то частоты сигналов f- и f+ можно найти по формулам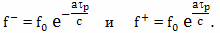
Таким образом, частота сигнала передаваемого с Земли, является средним геометрическим величин f+ и f-. То есть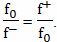
При этом, разница между частотами Δ+ = f+ - f0 всегда больше, чем разница между частотами Δ- = f0 - f-. Учитывая, что участки инерциального движения tи равны между собой и, по условиям парадокса близнецов, значительно больше, чем участки разгона tи >> tр, разницу между показаниями часов близнецов по окончании путешествия t-τ можно достаточно точно рассчитать по формуле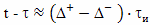
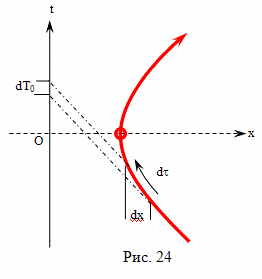
Ошибка при использовании этой формулы, будет связана с наличием ускоренных участков полета. То есть, это разница, которая возникла именно на участках прямолинейного и равномерного полета. К решению этой задачи можно подойти и с другой стороны, а, именно, принимать на Земле и анализировать сигнал, передаваемый с космического корабля на Землю (рис. 24). Можно видеть, что схема на рисунке 24 зеркальное отображение (относительно оси x) схемы на рисунке 22. И решение аналогично. Если излучаемый на космическом корабле сигнал имеет период T0, то принятый сигнал на Земле будет иметь период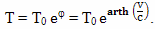
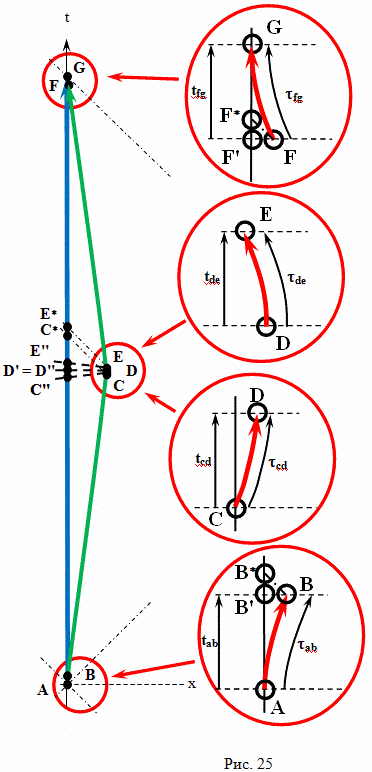
Если испускаемый космическим кораблем сигнал имеет частоту f0, то наблюдатель на Земле примет сигнал с частотой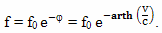
Только, в отличие от случая приема сигнала с Земли на космическом корабле, в случае, когда на Земле принимают сигнал с космического корабля, промежуток времени, в течение которого частота принятого сигнала меньще частоты переданного сигнала, больше промежутка времени, в течение которого частота принятого сигнала была больше частоты переданного сигнала. Чтобы выяснить это, достаточно взглянуть на схему на рисунке 25, на которой промежуток времени между событиями B* и С* явно больше промежутка между событиями E* и F*.
Если рассмотреть функцию частоты принятого сигнала от времени на Земле, то получится схема, похожая на ту, которая приведена на рисунке 26. Эта схема целым рядом деталей будет отличаться от схемы, приведенной на рисунке 23.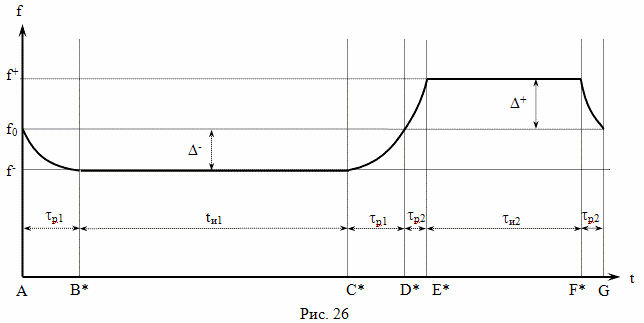
В этой схеме функция частоты от времени, на участках ускоренного движения космического корабля, уже не экспонента, а более сложная функция.
Участки инерциального движения τи1 и τи2 между собой не равны и, по условиям парадокса близнецов, значительно больше, чем участки разгона τр1 и τр2, разница между показаниями часов близнецов по окончании путешествия t-τ можно достаточно точно рассчитать по формуле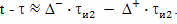
Таким образом, непосредственное наблюдение с Земли, как и непосредственное наблюдение с космического корабля, не дают никаких данных об особом ходе времени в ускоренно движущейся физической системе. Наоборот, частота сигнала принимаемого на Земле, как и сигнала, принимаемого на космическом корабле, зависит только от относительной скорости этих объектов и никак не зависит от величины ускорения космического корабля. И все это свидетельствует против объяснения парадокса близнецов, предложенного Альбертом Эйнштейном.
Цитируемая литература: [1] Альберт Эйнштейн Собрание научных трудов в четырех томах. Под редакцией И. Е. Таммма, Я. И. Смородинского, В. Г. Кузнецова. Том 1. Работы по теории относительности (1905-1920) Серия: "Классики науки". Изд. "Наука" Москва 1965 г. [2] Альберт Эйнштейн Собрание научных трудов в четырех томах. Под редакцией И. Е. Таммма, Я. И. Смородинского, В. Г. Кузнецова. Том 2. Работы по теории относительности (1921-1955) Серия: "Классики науки". Изд. "Наука" Москва, 1966 г. [3] А. С. Эддингтон "Теория относительности" ОНТИ Государственное технико-теоретическое издательство Ленинград, Москва, 1934г. [4] Макс Борн "Эйнштейновская теория относительности", изд.2-е, испр. Издательство "Мир", Москва, 1972 г. [5] Угаров В. А. "Специальная теория относительности", изд. 2-е, пер. и доп. Издательство "Наука", главная редакция физико-математической литературы, Москва, 1977 г. [6] Окунь Л. Б. "Понятие массы", журнал "Успехи физических наук" Июль 1989 г., стр. 511. Официальный сайт журнала http://ufn.ru/. [7] Бёрке У. (William L. Burke) "Пространство-время, геометрия, космология". Пер. с англ. - Москва: Мир, 1985. [8] Рейхенбах Ганс "Направление времени". Пер. с англ. Изд 2-е стереотипное. - Москва, Едитория УРСС, 2003. [9] Н. А. Черников "Геометрия Лобачевского и релятивистская механика". Физика элементарных частиц и атомного ядра, 1973, том 4, Вып. 3. Объединеный институт ядерных исследований, Дубна. [10] Н. А. Черников "Трудные вопросы теории относительности". Физика элементарных частиц и атомного ядра, 1987, том 18, Вып. 5. Объединенный институт ядерных исследований, Дубна. [11] В. Н. Дубровский, Я. А. Смородинский, Е. Л. Сурков "Релятивистский мир".- М.: Наука, Главная редакция физико-математической литературы, 1984. (Библиотечка "Квант". Выпуск 34. [12] Я. П. Терлецкий "Парадоксы теории относительности". изд.Наука, Москва 1966 г. [13] А. И. Жуков "Введение в теорию относительности". Государственное издательство физико-математической литературы, Москва 1981 г. [14] В. Курганов "Введение в теорию относительности", пер. с франц. В. Д. Захарова. Изд. "Мир", Москва 1968г. [15] Ф. С. Завельский "Масса и ее измерение". М.: Атомиздат, 1974. [16] Эйнштейновский сборник 1974. Ответственные редакторы В. Л. Гинсбург и Г. И. Наан, Составитель У. И. Франкфурт, Акадкмия Наук СССР, Отделение ядерной физики, Москва, Издательство "Наука", 1976 г. [17] Р. Толмен "Относительность термодинамика и космология". Пер с английского. Под ред. Я. А. Смородинского. Изд. Наука, Главная редакция физико-математической литературы, Москва 1974. [18] Л. Д. Ландау Е. М. Лифшиц "Теоретическая физика в десяти томах. Том II. Теория поля". Изд. седьмое, исправленное. Москва, "Наука", Главная редакция физико-математической литературы 1988 г. [19] Нинул А. С. Тензорная тригонометрия. Теория и приложения. - М.: Мир, 2004.
|