ОГЛАВЛЕНИЕ
Введение
Глава первая. КРИТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ И ЭЛЕМЕНТЫ КИНЕМАТИКИ ТЕОРИИ ДВИЖЕНИЯ
1.1. Необходимость модернизации теории относительности
1.2. Основные ошибки и упущения СТО
1.3. Новое определение скорости движения во времени и основное уравнение
теории движения
1.4. Что такое интервал и новое определение осей координат четырёхмерного пространства-времени, возвращающее его к эвклидовой геометрии
1.5. Основная диаграмма теории движения
Выводы к главе
Глава вторая. ЭЛЕМЕНТЫ ДИНАМИКИ ДВИЖЕНИЯ ВО ВРЕМЕНИ
2.1. Закон сохранения количества движения во времени
2.2. Вывод важнейших формул СТО
2.3. Что такое энергия покоя тела?
2.4. "Импульс покоя" тела и особые скорости движения
2.5. Что такое силы инерции?
Выводы к главе
Глава третья. ЭНЕРГИЯ В ТЕОРИИ ДВИЖЕНИЯ
3.1. Что такое энергия движения во времени?
3.2. Можно ли использовать энергию движения во времени?
3.3. Экскурс в релятивистскую термодинамику
3.4. Попытка прорыва вульгарного понимания закона сохранения энергии
Выводы к главе
Глава четвёртая. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
4.1. Абсолютность вращательного движения
4.2. Достижимость сверхсветовых скоростей при вращательном движении
4.3. Вращение разрешает парадокс движения во времени и даёт разгадку формулы Эйнштейна
4.4. Релятивистское обобщение теоремы вириала требует энерговыделения при ускорении вращения тел
4.5. Возможности выделения энергии связи при вращении тел
Выводы к главе
Глава пятая. МНИМОСТЬ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ И ТОРСИОННЫЕ ПОЛЯ
5.1. Энергия и импульс вращательного движения
5.2. Точки над I расставляют треугольники импульсов
5.3. Загадочные торсионные поля
5.4. Волны де Бройля и торсионные поля
Выводы к главе
Глава шестая. ВИХРЕВОЕ ДВИЖЕНИЕ ГАЗОВ И ЖИДКОСТЕЙ
6.1. Загадки атмосферных вихрей
6.2. Вихревой эффект Ранке
6.3. Парадоксы вихревой трубы
6.4. Гипотеза противотока в вихрях
Выводы к главе
Глава седьмая. ОТ ПУЛИ ДО СОЛНЦА
7.1. "Вечные двигатели" второго рода
7.2. "Антигравитация" гироскопов
7.3.0 механизме превращения тепла в энергию движения тел при их вращении
7.4. Несохранение чётности в атомных излучениях и "антигравитация"
7.5.0 связи вращения тел с их поступательным движением
7.6. От вихревой трубы до Солнца
7.7. Самые устойчивые вихри, ячейки Бенара и гранулы Солнца
Выводы к главе
Глава восьмая. ТЕПЛОВЫЕ НАСОСЫ
8.1. Почему тепловые насосы не прижились для теплоснабжения
8.2. Попытка сыграть на зависимости теплоёмкости воды от давления
8.3. Вихревая труба в тепловых насосах
Выводы к главе
Глава девятая. ВОДА КАК ИСТОЧНИК ТЕПЛА
9.1. Откуда энергия в воде?
9.2. Необыкновенные свойства обыкновенной воды в вихревом потоке
9.3.Капиллярная вода и вихревой теплогенератор
9.4. Вода вместо бензина - это реально
Вы воды к главе
Глава десятая. О ХОЛОДНОМ ЯДЕРНОМ СИНТЕЗЕ
10.1. Ядерно-энергетическая проблема
10.2. Холодный термояд - советское открытие?
10.3. Основная идея холодного ядерного синтеза
10.4. Гипотеза, оказавшаяся теорией
10.5.0 роли спина при ядерных взаимодействиях
Выводы к главе
Глава одиннадцатая. НОВЫЙ ПОДХОД К ХОЛОДНОМУ ЯДЕРНОМУ СИНТЕЗУ
11.1. Таинство электронного захвата
11.2. Гипотеза о синтезе дейтерия в воде
11.3. Нейтринный двигатель для космических кораблей
11.4. Осевое ионизирующее излучение вихревого теплогенератора - ещё одно проявление несохранения чётности?
Выводы к главе
Глава двенадцатая. ЗАГАДКИ СОНОЛЮМИНЕСЦЕНЦИИ
12.1. Ускорительный механизм холодного ядерного синтеза
12.2. Чудо сонолюминесценции
12.3. Электрические теории сонолюминесценции и явление Кезиковых
12.4. Особенности разрядов в сонолюминесцирующих пузырьках
12.5. Химические процессы при сонолюминесценции
12.6.0ткуда в земной атмосфере кислород?
Выводы к главе
Глава тринадцатая. ОТ СОНОЛЮМИНЕСЦЕНЦИИ К ЯДЕРНОМУ СИНТЕЗУ В КАВЕРНЕ
13.1. Кавитационная сонолюминесценция в потоке без ультразвука
13.2.0 предпороговом свечении, концентрировании энергии звукового
поля и ультразвуковой эмиссии нейтронов
13.3. Эффект Колдамасова
13.4. Соноэлектролюминесценция в каверне - торе
13.5. Об ошибке волгодонца и трудностях теории дейтрона
13.6. Гипотеза о квазинейтральном дейтроне, или к разгадке десятилетней загадки
Выводы к главе
Глава четырнадцатая. ЯДЕРНЫЕ ТРАНСМУТАЦИИ
14.1. Гипотеза о квантовых скачках протонов сквозь ядра атомов в молекулах
14.2. На пути к ядерным трансмутациям
14.3.Ядерные трансмугации - процесс молекулярный
Выводы к главе
Глава пятнадцатая. ВИХРЕВОЙ ТЕПЛОГЕНЕРАТОР
15.1. История создания вихревого теплогенератора
15.2. Тепловые установки "ЮСМАР"
Глава шестнадцатая. ТЕОРЕТИЧЕСКИЕ ПРВДПОСЫЛКИ
16.1. Теорема вириала требует энерговыделения при ускорении вращения тел
16. 2. Как излучает синхротрон?
16.3. Цель - внутренняя энергия вещества
16.4. Торсионные поля
16.5. Квант торсионного поля и химические реакции
Глава семнадцатая. ТЕПЛОГЕНЕРАТОР ПОТАПОВА- РЕАКТОР ХОЛОДНОГО ЯДЕРНОГО СИНТЕЗА
17.1. Кавитация как заменитель атомной бомбы
17.2. Как рождается дейтерий
17.3. Туннелирование по Сапогину
17.4. Ядерная реакция, ведущая к научному открытию
17.5. Разгадка десятилетней загадки
Глава восемнадцатая. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
18.1. Регистрация направленного у-излучения
18.2. Эксперименты с добавками тяжелой воды
18.3. Измерение скорости наработки трития
18.4. Регистрация нейтронов
18.5. Теплогенератор на морозоустойчивых жидкостях
18.6. На очереди - нейтринный "прожектор"
Глава девятнадцатая. КВАНТОВЫЕ ТЕПЛОЭЛЕКТРОСТАНЦИИ
19.1. Человечество осознает необходимость рачительно использовать энергоресурсы
19.2. Как устроена квантовая теплоэлектростанция
19.3. Как работает квантовая теплоэлектростанция?
Глава двадцатая. КВАНТОВЫЕ ВЕГРОЭНЕРГОСТАНЦИИ
20.1. Существующие варианты ветростанций
20.2. Устройство роторно-квантовой ветроэнергостанции
20.3. Принцип работы квантовой ветростанции
20.4. Примеры расчета опор и фундаментов для роторно-квантовой ветроэнергетической установки
Глава двадцать первая. ПЛАВАЮЩИЕ КВАНТОВЫЕТЕПЛОЭЛЕКТРОСТАНЦИИ
21.1. Особенности плавающих электростанций
Глава двадцать вторая. КВАНТОВЫЕ ДВИГАТЕЛИ
22.1. Может ли вода служить топливом?
Глава двадцать третья. АВТОНОМНЫЕ ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ
23.1. Энергия из воды и воздуха
Заключение
Приложение
Поэтому никто из восходивших на вершину теории относительности не догадывался, что вершина эта - двойная, как Эльбрус на Кавказе. Что стоит лишь вовремя свернуть с протоптанной тропы в туман неизведанного, как можно выйти на вторую вершину горы. Вторая вершина - это теория движения во времени. На эту вершину еще никто не восходил. Но пусть это не смущает читателя. И пусть не пугает обилие формул в книге. Эти формулы довольно простые, а их вывод дается тут же. Да и не формулы главное в данной книге. Они лишь помогают компактно выразить мысль.
И вовсе не обязательно знать теорию относительности, чтобы понять теорию движения во времени. Наоборот, тем, кто не знаком с теорией относительности, эта книга дастся легче. Заодно читатель легко и просто освоит основные положения теории относительности, которая обычно столь трудна для понимания. Ибо теория движения во времени позволяет взглянуть на теорию относительности с новой стороны и делает ее простой и понятной.
Читатель не найдет в данной книге рецептов для создания "машины времени". А вот о новых подходах к решению энергетической проблемы в ней говорится немало. Это может привести читателя к новым идеям в данной области. Приводится много размышлений о пространстве, в котором мы живем. Ну и, конечно, о времени как неотъемлемом свойстве этого пространства. Излагаются несколько иные, чем в теории относительности, представления о пространстве-времени. Ведь теория относительности изучала его только с одной стороны, только со своей вершины, а у нас появилась возможность взглянуть и с другой.
Теория движения во времени, с которой познакомит данная книга, позволит не только упростить изложение и понимание теории относительности, но и шагнуть дальше. Это говорит о том, что теория движения во времени - не просто игра досужего ума, а эффективный инструмент познания природы. Можно ли обойтись без нее? Теория относительности 90 лет пыталась обойтись без нее и только теряла от этого. Теория элементарных частиц, потребность в которой давно ощущает физика, без теории движения во времени так и не была создана. Мы видели, что суперквантование энергии движения во времени без каких-либо дополнительных условий ведет к чему-то похожему на теорию элементарных частиц.
Дополнительных предположений, конечно, не избежать. Одним из главных тут может явиться предположение о закономерностях, определяющих величину постоянной тонкой структуры. Среди этих закономерностей не последнюю роль будет играть золотое сечение, на которое указывает теория движения во времени и тайны которого приоткрывает эта книга.
Авторы полагают, что именно так может быть построен мост между электродинамикой и теорией гравитации, ведущий к созданию единой теории поля, о которой так мечтал Эйнштейн. Ну а мостить дорогу к ней будет теория движения во времени, или просто теория движения, как правильнее будет ее называть. Потребуется, правда, существенно доработать и осмыслить тот ее раздел, который описывает комплексное пространство. Сколько листов в этом многолистном комплексном пространстве? Тут мы видим, как мало мы еще знаем на этом этапе развития человечества.
Да, теория движения, судя по всему, станет вещью могучей. Но не будем обольщаться заранее. Ибо каждая теория - это только модель, в большей или меньшей степени отражающая окружающую нас природу или какие-то явления в ней.
доктор технических наук, профессор, заслуженный
деятель науки и техники Республики Молдова,
Лауреат Государственной премии РМ.
Отмечая 275-летие Российской Академии наук, её руководители постеснялись вспомнить о задаче, поставленной перед ней энергичным императором, хотя могли не только вспомнить, но и торжественно доложить, что это задание наконец-то выполнено.
Постеснялись потому, что ещё к середине XVIII века учёные осознали, что "вечный двигатель" первого рода (машина, которая, будучи раз пущенной в ход, совершала бы работу неограниченно долго, не потребляя энергию извне) противоречит закону сохранения энергии. Парижская Академия наук ещё в 1755 г. вынесла решение впредь не принимать к рассмотрению проекты "вечных двигателей".
А через 100 лет, после того как Р.Клаузиус сформулировал закон возрастания энтропии, объявили невозможным и "вечный двигатель" второго рода - воображаемую машину периодического действия, которая целиком превращала бы в работу всю теплоту, получаемую от какого-либо внешнего источника, например, моря или реки. Такой "вечный двигатель" противоречил бы второму началу термодинамики.
С тех пор "вечными двигателями" всерьёз занимались только отдельные чудаки, либо не слышавшие о первом и втором началах термодинамики, либо не желавшие смириться с догмой, поскольку в основе того и другого лежат постулаты - утверждения, которые невозможно ни доказать, ни опровергнуть, а требовалось принять на веру. В патентных ведомствах всего мира поставили корзины, куда без рассмотрения препровождали проекты "вечных двигателей".
Не исключено, что в эти корзины кануло немало проектов и реально работавших или способных работать устройств, названных их авторами или экспертами "вечными двигателями" лишь потому, что непонятно было, откуда в них появляется движущая сила, каков её источник. Вот и приходили к заключению, что при работе этих устройств энергия должна рождаться из ничего, а значит "этого не может быть, потому что не может быть никогда", даже если устройство и работало.
А ведь при оценке проектов исходили лишь из знаний своего времени, забывая, что уровень сегодняшнего знания скорее можно назвать уровнем незнания, и в Природе имеется ещё столько непознанного, что не для одной эпохи хватит познавать. Так, ещё 100 лет назад люди ничего не знали о внутренней энергии вещества и ядерной энергии, а 200 лет назад электричество считали нематериальным, и никому не приходило в голову использовать электроэнергию.
Если бы в XVIII веке на суд Парижской Академии наук был представлен электромотор, то его проект был бы объявлен проектом "вечного двигателя", ибо тогда не знали, что энергию можно передавать по тонким металлическим проводам без видимого движения чего-либо.
Вихревой теплогенератор, о котором пойдет речь в данной книге, мог быть создан ещё в петровские времена - технических возможностей для этого хватало уже и тогда. Но появился он лишь в конце XX века. Да и то эксперты патентных ведомств; косились - уж не очередной ли проект Pertpetuum mobile? Пришлось при оформлении заявки на патент умалчивать, что эффективность этого устройства для нагрева воды механическим перемешиванием - свыше 100%, и скрывать, что тепла оно вырабатывает больше, чем потребляет электроэнергии двигатель насоса, подающего воду в устройство (единственный в нём потребитель энергии).
Автор теплогенератора догадывался, что энергия тут появляется отнюдь не "из ничего", что в энергию превращается ничтожная часть массы циркулирующей в теплогенераторе воды согласно знаменитой формуле Эйнштейна Е = mС2. Но поскольку все считали, что в окружающей нас природе такое превращение воды в энергию самопроизвольно не идёт, и только мечтали реализовать его в термоядерных реакторах будущего, то и автор вихревого теплогенератора сомневался в правильности своего предположения. Тем более что официальная академическая наука "ничем помочь не могла".
А в кругах её оппонентов в это время витали идеи о "неиссякаемой энергии физического вакуума", о холодном ядерном синтезе, о торсионных полях, сонолюминесценции и другие. И каждый из сторонников этих идей предлагал принять на веру, что именно данная идея работает в вихревом теплогенераторе, обеспечивая появление в нём "лишнего" тепла. Тем не менее, никто из них не мог представить конкретные расчёты, объясняющие если не количественно, то хотя бы качественно процесс рождения "лишнего" тепла.
Никому и в голову не приходило, что тут могут работать релятивистские эффекты теории относительности. Считалось, что релятивистские эффекты заметно проявляются только при околосветовых скоростях движений, а не при технических скоростях, какие имела вода в вихревом теплогенераторе.
В отличие от экспертов, потребители быстро поняли преимущества нагрева воды вихревым теплогенератором по сравнению с нагревом обычными электрическими кипятильниками. Но производственники поначалу осторожничали ставить на серийное производство такой теплогенератор, в котором неизвестно откуда берётся тепло, резонно опасаясь, что тогда неизвестно откуда может появиться и нейтронное излучение, убийственное для всего живого. Вспыхнувший за несколько лет до того ядерный пожар Чернобыля заставлял многих, обжёгшихся на нём, "дуть теперь на воду". Требовалась теория, объясняющая работу вихревого теплогенератора и показывающая его безопасность. Такова уж особенность нашего просвещенного времени, что без должной теории новое устройство обречено на неприятие обществом.
Теория вихревого теплогенератора, указывающая на главную причину появления в нём "лишнего" тепла, могла быть разработана ещё в 20-е годы - сразу после появления теории относительности. Но почитатели теории относительности в те годы принципиально не хотели заниматься вращательным движением, резонно опасаясь, что это может нанести вред "стройному зданию" "красивейшей теории", построенному Эйнштейном и его последователями на шатком основании двух недостаточно проверенных постулатов Эйнштейна. Вращательное движение с самого начала не укладывалось в прокрустово ложе теории относительности с её отрицанием абсолютного движения и возможности сверхсветовых скоростей.
Ведь вращательное движение ещё со времен Ньютона признавалось абсолютным, в отличие от поступательного, которое считалось относительным. Считалось до тех пор, пока в 1979 г. после открытия реликтового микроволнового излучения не была зарегистрирована скорость движения Земли относительно него, названная абсолютной скоростью движения Земли в мировом пространстве.
Потребовалось появление теории движения, позволившей взглянуть на теорию относительности как бы с другой стороны и существенно дополнившей её, попутно исправляя и упрощая, чтобы причина появления "лишней" энергии в вихревом теплогенераторе стала прозрачно понятной. Удивительно, что теория движения родилась в те же 90-е годы, когда появился вихревой теплогенератор и независимо от него, хотя могла бы появиться ещё в 20-е годы.
Нет, теория движения создавалась не для объяснения работы вихревого теплогенератора. Наоборот, вихревой теплогенератор - это только одно из практических применений теории движения. Она потому и названа просто теорией движения, что описывает все виды движений, как поступательное, так и вращательное, как в пространстве, так и во времени. Предельно простое основное уравнение теории движения ?2 + у2 = 1 неслучайно испокон веку считается в математике одним из красивейших канонических уравнений, а основная диаграмма теории движения, описываемая этим уравнением, возможно, станет символом науки третьего тысячелетия, как планетарная модель атома стала символом науки XX века.
Обычно появление теории и практическое воплощение её в металле далеко во времени отстоят друг от друга. А тут - такая поразительная одновременность! И ещё удивительно, что авторы вихревого теплогенератора и теории движения нашли друг друга в 1999 г. - в год юбилея Указа российского императора, и оба оказались русскими, хотя и живущими теперь, увы, в разных странах: один в Молдове, другой - в Украине.
Да и для всего Человечества это открытие поистине неиссякаемого источника даровой энергии оказывается сейчас как нельзя кстати. Ведь запасы органического топлива - традиционного источника энергии на Земле - уже иссякают. Нефти, угля, и природного газа, по оценкам экспертов, осталось лет на 30 не более, если и дальше продолжать добывать их в прежних объёмах. Но это недопустимо. И не только потому, что они - ценнейшее сырьё для химической промышленности, и сжигать нефть - это, как говорил Д. И. Менделеев, всё равно, что топить печь ассигнациями. Недопустимо ещё и потому, что то положение, которое сложилось с экологией на нашей планете в результате всё нараставшего сжигания органических веществ, уже сегодня можно назвать критическим, предшествующим глобальной энергетической и эколого-климатической катастрофе.
Загрязнение окружающей среды вредными продуктами деятельности человека достигло красной черты. Наибольший удельный вес среди всех загрязнителей занимают продукты сгорания органических топлив. А ими наибольшее загрязнение воздуха в настоящее время осуществляют автомобили. Известный немецкий писатель Г.Хефлинг в своей книге с провидческим заголовком "Тревога в 2000 году", изданной в Германии ещё в 1981 г. и переизданной в Москве (издательство "Мысль") в 1990 г., пишет, что автомобили осуществляют до 40% общего загрязнения воздуха планеты. Академик РАЕН И.Л.Варшавский подсчитал, что каждый бензиновый или дизельный двигатель выбрасывает в атмосферу до 150 наименований отравляющих и вредных веществ. Среди них больше всего угарного газа (по данным Г.Хефлинга, только в ФРГ автомобили выбрасывают его 4,4 млн. тонн в год), окислов азота (1,8 млн. тонн в год только в ФРГ), двуокиси серы (0,1 млн. тонн).
Наиболее же опасны для человека соединения свинца, выбрасываемые из выхлопных труб автомобилей, использующих этилированный (содержащий свинец) бензин. В наше время в мире ежегодно выплавляется 3,5 млн. тонн свинца. Свыше 250 тысяч тонн из них, по данным Г.Хефлинга, ежегодно выбрасывается в воздух с выхлопными газами автомобилей, которые являются причиной появления 98% свинца, содержащегося теперь в воздухе планеты. Исследования образцов льда ледников в Гренландии показали, что в 60-е годы содержание свинца в воздухе стало в 400 раз больше, чем было до рождения Христова, и продолжает стремительно увеличиваться с ростом парка автомобилей на Земле. Палеонтологи обнаружили, что скелет человека конца XX века содержит свинца уже в 1000 раз больше, чем кости людей, живших тысячу лет назад. А американские медики утверждают, что дети, у которых найдено повышенное содержание свинца в молочных зубах, имеют коэффициент интеллекта в среднем на 4,5 балла (по десятибалльной шкале) меньший, чем их ровесники со средним содержанием свинца.
Свинец и другие вредные вещества проникают в организм человека не только вместе с вдыхаемым воздухом, но и вместе с водой, которую пьёт человек, и в которую они попадают с атмосферными осадками. Посетив в 1989 г. Москву, британский премьер-министр М.Тэттчер жаловалась, что во многих продуктах питания, производимых в Великобритании, в том числе в знаменитом шотландском виски, содержание свинца превышает предельно допустимую концентрацию, за что Общий Рынок только в 1988 г. наложил штрафов на 600 миллионов фунтов стерлингов. По приглашению М.Тэттчер один из авторов данной книги ездил в 1989 г. в Лондон демонстрировать свой новый способ очистки воды (патент РФ ? 1721989), который эффективно и быстро освобождает её от малейших примесей ионов свинца, ртути, хрома и других тяжёлых металлов и даже от радионуклидов. Но согласитесь, что гораздо эффективнее было бы не очищать воду от загрязнителей, а освободить окружающую природу от источников загрязнения.
А пока что напора уличных смогов, рождаемых автомобилями, не выдерживает не только здоровье человека, но и мрамор, и бронза памятников в городах. В результате Рим, считающийся музеем под открытым небом, терпит огромные убытки и невосполнимые потери от быстрого разрушения памятников, простоявших до этого много столетий.
Такое тревожное положение требует немедленного пересмотра проблем и концепций автотранспорта и перевода его на энергоносители, не загрязняющие воздух вредными выбросами, в первую очередь свинцом.
Многие не знают, что серьёзнейшим, а точнее вторым по значимости после автомобилей источником загрязнения атмосферы являются печи в домах. Казалось бы, что люди испокон веку топили печи в своих жилищах, и от этого не случалось ничего страшного, кроме пожаров, изредка опустошавших эти жилища. Но думающие так забывают, что ещё до конца XIX века людей на Земле было меньше миллиарда, а сейчас уже 6 миллиардов. Количество домашних очагов за 100 лет возросло в шесть раз! Кроме того, во второй половине XX века крестьянство даже в СССР окончательно перешло с отопления дровами, ставшими в результате вырубки лесов дефицитом, к отоплению своих домов каменным углем. С этого времени над теми селениями, в которых нет центрального отопления, вместо легкого древесного дыма висит тяжёлый и едкий угольный, в безветренную погоду буквально удушающий поселения.
Частные домовладения отравляют воздух главным образом угарным газом (СО) и тонкой пылью (пеплом и сажей) из печей. По данным Г.Хефлинга, в 1974 г. домашние отопительные устройства только ФРГ выбрасывали в атмосферу около 4 млн. тонн угарного газа. С переходом на газовое отопление количество выделяемого горелками угарного газа отнюдь не уменьшилось. Уменьшилось лишь количество видимого дыма. А угарный газ невидим и не имеет запаха, отчего особенно опасен. Наиболее он опасен для людей, страдающих заболеваниями сердца и кровеносных сосудов, число которых постоянно растёт. По данным немецкой газеты "SUddeutsche Zeitung" от 24.01.88, в атмосферу ФРГ от всех источников выбрасывается 7 млн. тонн угарного газа в год. А по подсчётам Российских учёных, сжигание 1 кг природного газа даёт в конечном счёте до 5 кг отравляющих и вредных веществ, образующихся в воздухе и воде. Еще страшнее, что при горении уничтожается кислород. Поэтому продолжение сжигания органических топлив несовместимо с жизнью на Земле.
В районах с высокой плотностью населения, насыщенных транспортом и промышленностью, утверждает Г.Хефлинг, отопление домов производит 30% общего загрязнения воздуха. Это столько же, сколько загрязнений выбрасывает в воздух вся промышленность. Поэтому замена печей в домах вихревыми теплогенераторами, питающимися электроэнергией и вырабатывающими больше тепловой энергии на каждый потребляемый ими киловатт электрической, могла бы существенно повысить чистоту воздуха в населённых пунктах и сохранить кислород.
Это будет проще и дешевле, чем переход от печного отопления к централизованному ещё и потому, что не потребуется прокладки целой сети теплотрасс, строительство и эксплуатация которых обходятся недешево и доставляют много неудобств. Переход же от печного отопления к центральному, хоть и делает воздух в населённых пунктах чище, не решает всех проблем, потому что котельные и теплоэлектроцентрали, в которых достигается более полное, чем в печах домов, сгорание топлива с меньшим процентом выхода угарного газа, тоже являются крупными источниками загрязнения воздуха.
По данным Г.Хефлинга, угольная электростанция установленной мощностью 700 МВт, потребляющая в год около 1 млн. тонн каменного угля, содержащего обычно ~ 1% серы, при своей работе всего за 1 час выбрасывает в воздух до 5 т двуокиси углерода, 0,15 т окиси углерода, 7 т двуокиси серы, 1,7 т окислов азота, 0,05 т углеводородов и 0,7 т пыли, которая содержит вредные тяжёлые металлы. Последних ещё больше в продуктах сгорания мазута, на использование которого в последние годы переведены многие котельные и ТЭЦ. Неслучайно НПО "Тулачермет", обеспечивающее все страны СНГ феррованадием, добывает ванадий (очень токсичный металл) из зольных отвалов ТЭЦ.
"Дыхание" крупных тепловых электростанций ощущают не только жители городов, в которых расположены эти электростанции. Кислотные дожди, возникающие из-за выброса трубами ТЭЦ высоко в атмосферу соединений серы, выпадают на расстояниях и в сотни километров от этих труб. Они вызывают заболевания растений из-за частичного распада хлорофилла. Особенно страдают овощные культуры и деревья. По свидетельству немецкой газеты "Вельт", половина лесов ФРГ больна из-за этого. А в скандинавских странах "импортные" кислотные дожди, приносимые ветрами из ФРГ, превратили некогда чистые озёра в безжизненные водоёмы.
Изучая возможные опасности от сжигания топлива, многие иногда забывают том, что на сжигание 1 кг угля или дров расходуется более 2 кг кислорода из воздуха. Та же крупная ТЭЦ мощностью 700 МВт, сжигающая миллион тонн угля в год, "пожирает" более 2 млн. тонн кислорода. Кислород, как известно, вырабатывают растения, в основном леса. А лесов на Земле становится всё меньше. Поэтому запас кислорода в воздухе планеты (21 %) с каждым годом пополняется всё меньше, а потребление его на сжигание топлив постоянно возрастает.
Если верны органические теории происхождения нефти и каменного угля, тот кислород, который содержится в воздухе, был когда-то выработан растениями, а большая его часть - древними растениями, остатки которых превратились в каменный уголь и нефть. И сколько в недрах Земли содержится каменного угля и нефти, почти столько же, соответственно, в воздухе - кислорода. Соединяя их при сжигании, мы не только уменьшаем запасы органических веществ на Земле, но и обедняем запасы кислорода в воздухе. Поэтому запасы каменных углей и нефти в земных недрах - это воистину тот "золотой запас", который надо беречь как золотой запас, чтобы в один ужасный день не обнаружить, что дышать на планете скоро станет нечем из-за нехватки кислорода в воздухе.
Но это пока не самая страшная опасность из нависающих над Человечеством. Есть более насущная. Тепловые электростанции в настоящее время являются основным источником электроэнергии. Даже если добиться полного улавливания фильтрами на них пыли и вредных газов (что невозможно), то от необходимости выбрасывания ими в атмосферу углекислого газа (С02) - продукта сгорания углерода - никуда не деться. И хотя этот газ при небольших его концентрациях совершенно безвреден для организма человека, именно он таит сейчас наибольшую опасность для Человечества.
Г.Хефлинг утверждает, что за последние 100 лет содержание углекислого газа я воздухе планеты возросло на 14%, и это обусловлено увеличивающимся сжиганием топлив и мусора, а также вырубкой лесов, которые поглощали часть углекислого газа из атмосферы. Продолжение роста содержания С02 в воздухе планеты грозит привести в результате "парникового эффекта", возникающего из-за поглощения углекислым газом теплового излучения поверхности Земли, к повышению температуры на Земле, интенсивному таянию полярных льдов и ледников, повышению уровня мирового океана и климатической катастрофе.
Уже сейчас на Земле стремительно теплеет. К чему это может привести в ближайшие годы? Мировая метеорологическая наука признала, что ошиблась, пытаясь в недавнем прошлом ответить на этот вопрос. В конце 1997 г. метеорологи ведущих стран собрались в японском городе Киото, чтобы обсудить насколько опасно глобальное потепление климата. И пришли тогда к выводу, что можно особо не беспокоиться, а надо лишь потихоньку уменьшать выбросы в атмосферу газов, вызывающих парниковый эффект. И тогда, мол, мы без катастрофических скачков постепенно войдём в "новую мезозойскую эру". Снег и лёд на Земле растают, кругом будут цвести райские сады...
Через год, когда экологическая ситуация на Земле неожиданно обострилась самым жарким в истории Человечества летом 1998 года, вызвавшим засухи и голод в Африке, выяснилось, что убаюкивающие выводы учёные в Киото приняли под давлением представителей администрации США, которые пока вежливо попросили учёных не мешать Америке коптить небо: ведь сворачивание производства энергии грозит промышленности огромными убытками. Восторжествовала не научная истина, а коммерческий интерес. Теперь учёные покаялись в своей ошибке и обратились в ООН с просьбой пересмотреть прежние расчёты. Директор Программы ООН по окружающей среде К.Тепфер в 1998 г. заявил: "У нас уже есть более чем достаточно убедительных свидетельств того, что глобальные климатические изменения представляют огромный риск". Он призвал все страны принять экстренные меры по ограничению выброса в атмосферу парниковых газов.
В 1998 г. Министерство по чрезвычайным ситуациям РФ прогнозировало, что в 1999 г. на общее потепление климата наложится малоизученное явление "Эль-Ни-ньо" - разогревание поверхности океанов. Оно увеличит частоту аномально жаркой погоды, ураганов и сильных снегопадов. Создадутся трудности в прогнозировании погоды. Лето 1999 г. в Евразии было рекордно засушливым, а осенью Земной шар тряхнули сокрушительные землетрясения. Вы спросите причём тут землетрясения? Не спешите с выводами!
Все это десять лет назад предсказывал военный инженер из г.Волжский Г.И.Митяков. Несколько лет он бесплодно обивал пороги министерств и ведомств, пытаясь убедить чиновников в чрезвычайной опасности стремительного потепления климата и принять меры, пока ещё не поздно. Он утверждал, что когда в результате таяния полярных ледников вода стечёт в океаны и их уровень поднимется, экваториальные области Земного шара из-за этого станут тяжелее, чем полярные, и Земной шар "кувыркнется" - изменится положение его оси вращения. В Сибири будут тропики, а в США - Северный полюс. Такая катастрофа, которая может случиться уже в ближайшее столетие, будет означать конец нашей цивилизации. Об этом предупреждении Митякова рассказала московская газета "Рабочая трибуна" в номере от 05.08.97. Увы, предупреждение не было услышано. А Земной шар уже начинает содрогаться. И Венецию уже затопляет, и многие коралловые рифы уже погрузились под воду. Многие учёные теперь приходят к выводу, что ситуация зашла слишком далеко и Человечество уже не успеет принять меры к спасению. Ведь ничто, казалось бы, не может заставить людей резко уменьшить сжигание топлива. Для этого потребовалось бы чудо.
И такое чудо произошло: был изобретен и поставлен на производство вихревой теплогенератор, способный в полтора раза уменьшить сжигание топлив для получения того же количества тепла. Возможно, он поможет предотвратить очередной Всемирный потоп на Земле.
Нас спросят: а как же атомная энергетика? Ведь атомные электростанции не жгут органическое топливо, не загрязняют небо дымом и не выбрасывают в него коварный углекислый газ! И они уже сегодня во многих странах, например во Франции и в Украине, производят чуть ли не половину всей вырабатываемой электроэнергии. Может, ядерная энергетика - путь к спасению от Всемирного потопа?
По крайней мере, полтора десятка лет назад так думали многие. Но чернобыльская катастрофа 1986 г. убедительно показала всему миру, что ядерная энергетика - это подмена одной проблемы другой. Ядерная опасность не менее серьёзна, чем опасность перегрева атмосферы в результате сбрасывания в неё углекислого газа. Заражение поверхности планеты радиоактивными веществами в результате катастроф, подобных чернобыльской, лишит людей жизненного пространства и обречёт их и всё живое на Земле на вымирание в результате мутаций и онкологических заболеваний. Излечить поверхность Земли от радиоактивного загрязнения не легче, чем атмосферу от перегрева. Даже если исключить повторение катастроф, подобных чернобыльской (что маловероятно), развитие ядерной энергетики всё равно приведёт к загрязнению окружающей природы радиоактивными изотопами. Ведь радиоактивные отходы ядерной энергетики не отправляют на другие планеты, а захороняют на Земле, и захороняют не очень надежно. Иногда их просто сбрасывают в море, полагая, что морская пучина всё спрячет. И до сих пор стоят переполненными радиоактивные пруды-отстойники рядом с заводами по производству ядерного топлива, готовые прорваться в реки при первом же наводнении. Эту воду, кстати, тоже можно очистить от радионуклидов с помощью изобретения по патенту РФ ? 1721989, но никто почему-то не спешит это делать. Беспечность по отношению к радиоактивному загрязнению планеты столь же высока, как и беспечность по отношению к загрязнению воздуха углекислым газом.
Ядерная энергетика - вещь чересчур рискованная, чтобы делать на неё ставку. Да и запасов урана и тория - ядерных "топлив", пригодных для промышленной добычи, на Земле не так уж много, как думают многие. Лет на 30 всего, если существующие темпы роста энергопроизводства сохранятся. А они не могут снизиться, ибо численность населения на Земле продолжает расти. Нас уже 6 миллиардов, которых надо и накормить, и одеть, и согреть.
Всё это настойчиво показывает острую необходимость поиска и скорейшего освоения альтернативных источников энергии, таких, как энергия ветра, морских приливов, солнечных лучей и, конечно же, внутренней энергии вещества, извлекаемой без ядерных реакций, вызывающих радиоактивное загрязнение окружающей среды. К числу альтернативных и относится вихревая энергетика, первой ласточкой которой явился вихревой теплогенератор.
Конечно, старое никогда не уступает новому. Топливно-энергетический комплекс, в самом названии которого навязывается людям мысль о якобы неразрывной связи между необходимой им энергией и неизбежностью сжигания для этого топлив, бурно развивался последние 200 лет и не сдаст своих позиций без сопротивления. Об этом говорят полутрагические и поистину трагические судьбы Н. Теслы, В. Шаубергера, К.Э.Циолковского, А. Л.Чижевского, А.И.Вейника, В.И.Докучаева, И.С.Филимоненко, С.Маринова, Б.В.Болотова и многих других разработчиков альтернативной энергетики, которых "огнепоклонники" полупрезрительно называли изобретателями "вечных двигателей" и ниспровергателями второго начала термодинамики.
Но приходит время, когда сама жизнь заставляет нас обратить внимание на новые источники энергии, которые придут на смену старым способам добычи тепловой и электрической энергии.
КРИТИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ И ЭЛЕМЕНТЫ КИНЕМАТИКИ ТЕОРИИ ДВИЖЕНИЯ
До настоящего времени существовала созданная гением Галилея, Ньютона, Лейбница, Лагранжа, Гюйгенса и других классическая механика с её динамикой и кинематикой, а также созданная в начале XX века трудами Эйнштейна и его современников (Лоренца, Пуанкаре, Минковского и др.) релятивистская механика с ее представлением о четырехмерном пространстве-времени, в котором осуществляется движение тел.
Релятивистская механика, используемая в основном для расчетов движения элементарных частиц со скоростями, сравнимыми со скоростью света, имела дело только с досветовыми скоростями, поскольку специальная теория относительности (СТО), предложенная А. Эйнштейном в 1905 г. [1], постулировала, что в природе не существует скоростей движения больших, чем скорость света в вакууме С = 2,99792458 ? 108 м/с (второй постулат Эйнштейна).
В 60-е годы родилась идея тахионов - гипотетических частиц, движущихся со сверхсветовыми скоростями. Но для описания движения этих частиц разработчики теории тахионов использовали всё ту же релятивистскую механику, хотя она в данном случае далеко не всегда способна была дать требуемые и понятные результаты.
СТО имела дело преимущественно с прямолинейными и равномерными движениями, а при попытках решения задач, связанных с криволинейным или вращательным движением, пасовала и отсылала к общей теории относительности (ОТО), математический аппарат которой оказался слишком сложным и недоступным большинству инженеров. Да и перечень задач, успешно решенных ОТО, остается весьма ограниченным.
В результате теория относительности, называвшаяся многими в середине XX века красивейшей и величайшей теорией всех времен, до сих пор так и не принесла людям ожидаемых от нее грандиозных результатов. Хотя, конечно, создание кинескопа (электронно-лучевой трубки) телевизора, ускорителей элементарных частиц и ядерной энергетики, бывшее невозможным без теории относительности, - это бесспорно важные достижения, но ожидалось нечто большее. Вопреки ожиданиям, теория относительности, "забуксовав" еще в начале 20-х годов, с тех пор фактически так и не продвинулась вперед. Ее сторонники объясняли это законченностью и совершенством теории и создавали культ личности Эйнштейна. Критиковать его теорию считалось недостойным для настоящего ученого* (*Журнал "Молодая гвардия" в N 8 от 1995 г. на стр. 70 писал: "В 1964 г. Президиум АН СССР издает открытое постановление, запрещающее всем научным советам и журналам, научным кафедрам принимать, рассматривать, обсуждать и публиковать работы, критикующие теорию Эйнштейна").
Но критики теории относительности давно подметили в ней ряд внутренних противоречий и недоработок. Они обсуждаются, например, в книгах В.А. Ацюковского [2, 3], братьев Брусиных [4], известного французского ученого Л. Бриллюэна [5]. В предисловии к русскому изданию 1972 г. книги Л. Бриллюэна академик АН УССР А. 3. Петров незадолго до своей кончины писал: "Что касается ОТО, то, вопреки довольно широко распространенному мнению, могучее сооружение этой теории покоится на столь шатком экспериментальном фундаменте, что ее можно было бы назвать колоссом на глиняных ногах... Если, например, историческое развитие квантовой механики доказывает постепенное ее совершенствование, "взросление", все большее повышение ее точности благодаря накоплению экспериментального материала и включению его в теорию, то ОТО до сих пор щеголяет в коротких штанишках "вундеркинда", которому всё дозволено и даже - освобождение от экспериментальной проверки. Для истинного физика такое положение нетерпимо".
А вот в отношении СТО Петров там же отзывается только похвально, хотя СТО тоже полна парадоксов, а значит, внутренних противоречий. Наиболее известен из них "парадокс часов", или "парадокс близнецов", о котором написаны тысячи страниц.
Но в 1972 г. уже семь лет как было открыто реликтовое излучение, которое в 1979 г. позволило измерить абсолютную скорость движения Земли в космическом пространстве [6] и тем самым пошатнуть веру многих в незыблемость постулатов Эйнштейна, провозглашающих, что в природе не существует абсолютной (выделенной) системы отсчёта координат и абсолютных скоростей движения, что они только относительны. Появилось множество критиков и ниспровергателей Эйнштейна (большинство из которых - люди недостаточно компетентные и недостаточно самокритичные), называющих себя "нерелятивистами" и стремящихся любыми средствами опорочить и "отменить" теорию относительности. Но никто из них не сумел предложить взамен нее что-либо более простое, более общее, менее противоречивое и, наконец, более понятное.
В этой ситуации требовалось, с одной стороны, отстоять от необоснованных наскоков те моменты теории относительности, которые подтверждаются экспериментами и не противоречат ни логике, ни математике, а с другой стороны, выявить и отбросить все то ошибочное, что существовало в теории относительности, делало ее непонятной и противоречивой и сдерживало ее развитие.
Некоторые сторонники теории относительности тоже понимали необходимость перемен. Так, например, известный российский специалист по теории относительности Е. Л. Фейнберг в [7] выражал беспокойство о том, что традиционный кинематический подход к СТО делает её формальной наукой, занимавшейся математическими манипуляциями с физическими символами. Он указывал, что для улучшения понимания предмета надо бы исходить из динамических характеристик движения, и сетовал, что никто до сих пор этого не сделал.
В книгах [8] и [9] как раз и сделана попытка такого подхода для построения теории движения взамен СТО. Но прежде чем перейти к изложению основных положений теории движения, разберемся в некоторых ошибках и упущениях теории относительности.
1.2. Основные ошибки и упущения СТО
В теории относительности огромную роль играет представление о четырехмерном пространстве-времени и об интервале как расстоянии между точками в нем. В доэйнштейновские времена полагали, что пространство Вселенной трёхмерно и описывается эвклидовой геометрией с декартовыми осями координат х, у, г. Но когда описывают движение тела, например, когда чертят график движения поезда, то вдоль одной оси координат на листе бумаги откладывают расстояния, а вдоль другой - время t. Ось времени - четвертая ось координат - ещё с догалилеевских времён неявно присутствовала в описаниях движения тел, только люди не осознавали этого.
Первым осознал Г.Минковский, помогавший Эйнштейну создавать математический аппарат теории относительности. Он в 1908 г. и объединил пространство и время в единое четырёхмерное пространство-время.
Поскольку движения во времени из прошлого в будущее мы не видим, а только понимаем (мним), что оно существует, Минковской назвал четвёртую (временную) ось координат мнимой.
Если трехмерное пространство еще можно изобразить на листе бумаги с помощью изометрии, то четырехмерное уже невозможно. Но СТО первоначально рассматривала только прямолинейные и равномерные движения тел вдоль одной оси координат. Поэтому Минковский вслед за составителями графиков движения поездов стал откладывать на одной оси координат плоскости листа бумаги расстояния l в трехмерном пространстве, а на другой, перпендикулярной ей оси - мнимые "расстояния" во времени iСt Здесь символ
означает мнимую единицу, а на скорость света в вакууме С домножено для того, чтобы "расстояния во времени" имели ту же размерность (метры), что и расстояния в пространстве.
В результате получилась комплексная плоскость (l,iСt ), действительная и мнимая оси координат которой пересекаются в точке 0, принятой за начало отсчета координат. Всякая точка на такой плоскости в математике описывается комплексным числом
(1.1)
В последней длина вектора, или отрезка ?l, связана с длинами его проекций (?х, ?у, ?z) на декартовы оси координат теоремой Пифагора:
(1.2)
(1.3)
то данное выражение он переписал в виде:
(1.4)
равен разности квадратов катетов
И хотя треугольника такими свойствами не начертить даже с помощью неэвклидовой геометрии Римана, ссылки на которую любил делать Эйнштейн, объяснили, что такова уж особенность четырехмерного пространства-времени. Эйнштейн назвал это эфемерное пространство "квазиевклидовым" [10].
Для чего потребовалась столь смелая "модернизация" геометрии? Дело в том, что в классической механике преобразования Галилея при переходе от одной инерциальной системы отсчета координат к другой оставляли неизменным расстояния в трехмерном пространстве. Разработчикам СТО хотелось, чтобы по аналогии с этим используемые ими преобразования Лоренца, заменившие в СТС преобразования Галилея, оставляли неизменной (инвариантной) не только скорости света С (для чего они и были найдены X. Лоренцем), но и расстояние между точкам! четырехмерного пространства - времени [11]. Однако величина ?К, вычисляемся и; формулы (1.3) оставалась инвариантной при преобразованиях Лоренца только когда; в формуле (1.4) между ее слагаемыми был знак минуса. Более того, когда и само значение
брали со знаком минуса. В конце концов разработчики СТО записали:
(1.5)
Казалось бы, что все вроде правильно, хотя и требовало ломки сложившихся представлений эвклидовой геометрии, принятия без доказательств "псевдопифагоровой теоремы" и отказа даже от попыток наглядно представить происходящее в "псевдоевклидовом" пространстве. Но этот отрыв физики от наглядности скоро был объявлен не недостатком, а достижением теории.
Благодаря своей инвариантности, облегчающей расчеты, понятие интервала как расстояния между точками "четырёхмерного континуума" стало широко использоваться в СТО, а затем и в ОТО, где все зиждется на понятии об интервале. Но разберемся, насколько верно его определение.
Точку в четырехмерном пространстве-времени Минковского, называемом "миром Минковского", описываемую комплексным числом (1.1), в СТО называют "мировой точкой". При ее движении в пространстве - времени она рисует на плоскости листа бумаги "мировую линию".
Комплексная длина бесконечно малого отрезка этой линии, или дифференциал комплексного числа, в теории комплексных чисел определяется выражением [13]:
(1.6)
(1.7)
которую мы видели в формуле (1.4). Поэтому можно сделать вывод, что то выражение, которое в СТО называют квадратом дифференциала интервала dS и понимают его как квадрат бесконечно малого расстояния между точками пространства-времени, на самом деле является лишь взятой с противоположным знаком действительной частью квадрата бесконечно малого отрезка комплексной длины мировой линии.
А вот мнимая его часть
ускользнула от внимания разработчиков СТО. И только в ОТО мнимая часть выражения (1.7) была учтена, хотя разработчики ОТО так и не осознали, что интервал - это отнюдь не расстояние между точками пространства-времени. Но не будем углубляться в ОТО, а вернемся к комплексной плоскости мира Минковского, точку на которой описывает комплексное число (1.1).
В теории комплексных чисел расстояние между точками
комплексной плоскости вычисляют как модуль (абсолютную величину) разности
комплексных чисел, описывающих данные точки. Этот модуль определяют из теоремы Пифагора:
(1.8)
Чем же тогда на самом деле является так называемый интервал ?S, определяемый из выражения (1.5), если это не расстояние между точками пространства-времени?
Чтобы ответить на этот вопрос, надо, оказывается, сначала внимательно разобраться в том, как определять скорость движения в пространстве-времени. В классической механике среднюю скорость V движения тела в пространстве определяют как отношение длины пути
пройденного телом, ко времени ?t, за которое пройден этот путь. А мгновенную скорость V определяют как производную от l по dt (11. Если по аналогии с этим определять скорость движения точки в пространстве - времени "мира Минковского", то надо взять производную по dt от комплексного числа К, описывающего данную точку:
(1.9)
Г. Минковский нашел выход (к сожалению, как мы сейчас покажем, не наилучший) из этого затруднительного положения - стал определять скорость движения точки в пространстве-времени как производную от К по собственному времени
, отсчитываемому часами, перемещающимися вместе с движущимся телом! (измеряемому его собственными часами).
Ведь Эйнштейн уже в первой своей публикации [1] 1905 г. по СТО показал, что движущиеся часы должны идти медленнее неподвижных, и что при движении тела
? t в соответствии с его формулой
(1.10)
мнимая часта получающегося выражения уже не была константой. Определяемую так скорость; движения точки в пространстве-времени своего "мира" Минковский назвал "четырёхскоростью":
(1.11)
, которая инвариантна при преобразованиях Лоренца, что облегчало расчеты.
Физики и по сей день пользуются таким определением четырехскорости, записывая его, правда, в несколько ином виде:
(1.12)
Но обратим внимание на то, что мнимая (временная) часть четырехскорости в выражении (1.11) при V > О больше скорости света С и устремляется к бесконечности, когда V --?С. Да и действительная часть четырехскорости
возрастая с ростом скорости V, становится больше скорости света С, когда V превышает величину
Это как-то не очень вяжется с постулатом Эйнштейна, провозглашающим, что в природе не существует скоростей движений тел, больших скорости света в вакууме С. Разработчикам СТО не удалось найти выхода из этой щекотливой ситуации, и тогда четырехскорость (1.11) и была преобразована в безразмерную величину (1.12) чтобы хоть как-то завуалировать указанное противоречие.
А ведь оно возникает лишь от того, что величины l и
взяты из разных систем отсчета: l - из неподвижной, связанной с наблюдателем, относительно которого происходит движение,
- из движущейся, связанной с перемещающимся телом. Так определять скорость движения тела некорректно!
В книге [8] впервые дано новое определение мнимой скорости движения тела во времени, позволяющее освободить теорию относительности от указанных выше недочетов, которые более 80-ти лет сдерживали ее развитие. По аналогии с вышеприведенным классическим определением скорости V движения тела в пространстве, в [8] скорость у мнимого движения тела во времени выражается в секундах "пути"
во времени, проходимого телом за время t, отсчитанное часами наблюдателя, относительно которого движется данное тело. В результате получается безразмерная величина
(1.13)
(1.14)
= t, поэтому
А с увеличением скорости V движения тела величина
становится меньше, чем t, как это следует из эйнштейновской формулы (1.10) и из многочисленных результатов экспериментов по измерению времени "жизни" ускоренных элементарных частиц, проводившихся в разных странах с 40-х годов. Поэтому безразмерная скорость у движения тела во времени уменьшается с ростом скорости V движения его в пространстве, становясь меньше единицы при
Кстати, скорость движения тела в пространстве тоже можно преобразовать в безразмерную, если разделить V на С. Безразмерная скорость движения тела в пространстве
(1.15)
Анализ многочисленных экспериментов по измерению времени "жизни" неустойчивых к распаду элементарных частиц, ускоренных до самых разных скоростей V, проводившихся с 40-х годов, показывает, что во всех случаях соблюдается уравнение
(1.16)
Из нее понятно, что
этот радикал, фигурирующий в большинстве формул и уравнений СТО, долгие годы называли "фактором Лоренца", не догадываясь, го это еще и безразмерная скорость движения тела во времени.
В книге [8] величины
, являющиеся решениями уравнения (1.16), рассматриваются как действительная и мнимая части комплексной скорости движения тела
(1.17)
. Всякая точка на такой новой комплексной плоскости теперь будет описываться комплексным числом
(1.18)
Непривычной и необычной, на первый взгляд, получается наша новая комплексная плоскость, одна координата (l) на которой определяется измерениями одного наблюдателя, а другая (Сг) - другого, движущегося относительно первого. Но ведь это комплексная плоскость расстояний. Ее ось Ol - это ось расстояний в пространстве, которые проходит тело за время t, отсчитываемое часами неподвижного наблюдателя, другая же ее ось OiC
- это ось "расстояний" С
во времени, которые проходит то же тело за то же время t, отсчитываемое часами того же наблюдателя, относительно которого движется данное тело.
Определим теперь квадрат расстояния между точками 0 и Z нашей комплексной плоскости (l, iC
) как квадрат модуля комплексного числа
(1.19)
- уt, то с учётом уравнения (1.16) получим:
(1.20)
А вот если подставить полученное значение
вместо
в (1.19), будем иметь:
(1.21)
Впрочем, формулу dS = Cd
нам и доказывать не надо, она давно известна в СТО [14].
С учетом этого запишем окончательное выражение для квадрата расстояния ?
между точками нашего комплексного пространства-времени:
(1.22)
Эвклидова геометрия восторжествовала! И уже не нужны ни "псевдопифагорова теорема", ни "квазиэвклидовое пространство", бывшие, как мы теперь понимаем, вынужденными уловками разработчиков СТО на неосознанном ими пути к уравнению (1.22), задаваемому самой Природой.
Основное уравнение (1.16) теории движения является не чем иным, как каноническим уравнением плоской центральной кривой второго порядка
Если ß и у - действительные числа, то графиком уравнения (1.16) является окружность, имеющая радиус, равный единице (см. рис. 1.1). Эту окружность описывает вокруг начала осей координат на комплексной плоскости конец радиуса-вектора комплексной скорости
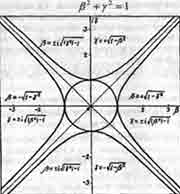
Рис. 1.1. Основная диаграмма теории движения (9).
(1.23)
Основное уравнение (1.16) при
и при ß -мнимом превращается в уравнение гиперболы:
(1.24)
Отметим, что абсолютные величины
удовлетворяющие уравнению (1.24), не имеют ограничений сверху. То есть они лежат в пределах
(1.25)
становится чисто мнимой величиной.
Как видим, скорости движения ß по своей абсолютной величине здесь могут называться за пределами дозволенного теорией относительности, то есть становятся больше единицы, а скорости у вообще всегда больше единицы, если ß - мнимое число. Поэтому области на рис. 1.1, описываемые верхней и нижней ветвями гиперболы (1.24), названы в книге [9] "вертикальным запредельным миром", в отличие от допредельного мира, описываемого единичной окружностью, характеризующей поступательное движение обычных тел с досветовыми скоростями.
Предположим теперь, что мнимым числом является величина безразмерной скорости у движения объекта во времени. Тогда основное уравнение (1.16) останется справедливым, если величина безразмерной скорости движения этого объекта в пространстве
(1.26)
(1.27)
И опять абсолютные величины безразмерных скоростей ß и у не имеют ограничений сверху:
(1.28)
Области на рис. 1.1, описываемые правой и левой ветвями гиперболы (1.27), названы в книге [9] "горизонтальным запредельным миром". В этом мире должно наблюдаться довольно странное явление. А именно, в результате того, что мнимая часть комплексной скорости J становится действительным числом, движение во времени тут становится реальным, а не мнимым! Это означает, что объект, совершающий такое движение, не может быть обнаружен ни в какой точке времени, так как непрерывно перемещается сквозь "пласты времени", как бы пересекая их. Если в данный момент (по нашим часам) он в течение какого-то мгновения, продолжительность которого определяется, по-видимому, соотношением неопределенностей квантовой механики, присутствует в нашем мире вместе с нами, то в следующий миг он уже во вчерашнем или в завтрашнем нашем дне, в то время как мы остались в сегодняшнем и медленно движемся в завтрашний вместе с окружающими нас реальными предметами нашего мира досветовых скоростей. В результате этот объект, который можно назвать виртуальным, сегодня для нас уже недосягаем и неуловим. В книге [9] показано, что правая и левая полуветви основной диаграммы теории движения описывают движение гипотетических сверхсветовых частиц - тахионов, теорию которых физики начали разрабатывать еще в 60-е годы [15]. Но экспериментаторам несмотря на многочисленные попытки, до сих пор не удалось зарегистрировать тахионы, по-видимому, в силу вышеуказанной их особенности движения во времени, делающей тахионы почти ненаблюдаемыми.
Понимание этой особенности, дающееся теорией движения, может теперь позволить экспериментаторам по-иному взглянуть на проблемы регистрации тахионов. Более того, теория движения, дающая новый мощный толчок развитию теории тахионов, указывает, что виртуальные частицы в квантовой теории поля - это тахионы что неуловимые гравитоны - это тоже тахионы, а потому гравитация распространяется со скоростями, на много порядков величины превосходящими скорость света вакууме. Более того, в книге [9] показано, что всепроникающие нейтрино - это, по видимому, тоже тахионы! А нейтрино уже зарегистрированы экспериментально. Значит, тахионы всё-таки можно регистрировать?
Теория движения показывает, что виртуальный мир сверхсветовых частиц должен быть столь же богат (если не богаче), как и наш мир досветовых частиц. Богаче с может быть хотя бы потому, что тахионы обладают способностью двигаться во врем< ни как вперед, так и назад (а мы - только вперед). В [9] развивается гипотеза украинского физика из г. Бердянска М.Т. Попова о том, что именно тахионы несут информацию из будущего, которую каким-то образом воспринимают ясновидцы гадалки.
В заключение данной главы отметим следующее. Если движение объектов в "горизонтальном запредельном мире" описывается чисто действительной скоростью, а движение объектов "вертикального запредельного мира" - чисто мнимой J, то читатели могут подумать, что объекты "вертикального запредельного мира" обнаружить еще сложнее, чем "горизонтального". Но четвертая глава покажет, что наоборот. Более того, читатели увидят, что с объектами "вертикального запредельного мира они имеют дело буквально на каждом шагу и хорошо с ними знакомы. Только вот достаточно ли хорошо?
2. Скорость движения тела во времени
следует определять подобно скорости движения его в пространстве
как производную от пути по времени t, измеряемому наблюдателем, относительно которого движется данное тело.
3. точку пространства - времени следует описывать не комплексным числом
, как это делал Г. Минковский, а комплексным числом
. Это значит, что четвертой осью координат пространства - времени является ось
, а не ось
.
4. Безразмерная скорость движения тела во времени y и безразмерная скорость движения его в пространстве
(где С - скорость света в вакуума) связаны основным уравнением теории движения
.
5. Кроме действительных решений (попарных чисел
), графиком которых является единичная окружность, основное уравнение теории движения имеет ещё два семейства мнимых решений, графиками которых являются гиперболы. При мнимых y основное уравнение описывает движение частиц со сверхсветовыми скоростями
(тахионов), а при мнимых ß - вращательное движение тела, имеющего в результате вращения скорость движения во времени y больше единицы.
ЭЛЕМЕНТЫ ДИНАМИКИ ДВИЖЕНИЯ ВО ВРЕМЕНИ
Все мы понимаем, что непрерывно движемся во времени из прошлого в будущее вместе с окружающими нас предметами. Тем не менее до сих пор не существует целостной теории движения во времени. Рождение таковой задерживало, как ни странно, изобретение часов. Ибо с появлением механических часов, стрелки которых "идут" мелкими шагами, люди стали говорить не о движении времени, а о "ходе времени", как еще раньше, с изобретением водяных и песочных часов - клепсидр, начали говорить о "течении времени", наблюдая за течением воды или песка в этих часах.
Поэтому, когда в 1905 г. А. Эйнштейн предложил СТО, он заявил, что из нее следует, что ход времени зависит от скорости движения в пространстве. Про движение во времени даже речи не было. Эйнштейн изучал закономерности движения в пространстве, а затем и само пространство. Исходя из только-только открытого тогда факта, что в природе не существует скоростей, больших скорости света в вакууме С, он говорил о "ходе времени".
Лишь в 1908 г. Г. Минковский, помогавший Эйнштейну разрабатывать математический аппарат теории относительности, догадался, что пространство и время взаимосвязаны, и объединил их в единое четырёхмерное пространство-время, в котором движутся все тела.
Однако четырёхскорость Минковского, о которой мы говорили в разделе 1.2, была далеко не лучшим изобретением СТО - ее недостатки слишком бросались в глаза. Поэтому после смерти Минковского в 1909 г. этим понятием пользовались редко. Потому-то все до сих пор говорят о "ходе времени", а не о движении во времени, упуская из-за этого из вида динамические параметры движения тел во времени.
Это все равно, что говорить "бег дороги" вместо "бег автомобиля по дороге". Некоторые скажут, что не видят особой разницы между этими двумя выражениями, поскольку движение - понятие относительное. Но все же на повороте заносит автомобиль, а не дорогу. Поэтому для безопасного движения автомобиля учитывают его скорость и массу (произведение этих величин называют импульсом), а не массу дороги.
Мы уже говорили, что Е. Л. Фейнберг в [7] выражал беспокойство о том, что аддиционный кинематический подход к СТО делает её формальной наукой. Он указал, что для улучшения понимания предмета надо бы исходить из динамических характеристик движения, и сетовал, что этого никто не сделал. Но сделать это, исходя
из динамических характеристик движения тел в пространстве, было, по-видимому, невозможно, а рассматривать динамические характеристики мнимого движения во времени никому, увы, и в голову не приходило до появления работы [8].
В ней впервые было показано, что если учесть динамические параметры движения тел во времени, как учитывают аналогичные параметры движения автомобиля по дороге, то в СТО, столь трудной для понимания, все становится очень простым и ясным.
Хотя мнимого движения тел во времени мы не видим, попробуем представить, что оно в какой-то мере подчиняется законам обычной классической механики, в которой скорость V перемещения тела в пространстве заменим скоростью у движения его во времени. По аналогии с известным уравнением закона сохранения обычного импульса (количества движения) Р = mV в системе центра инерции
(2.1)
(2.2)
Мы воспользовались частным случаем уравнения для закона сохранения импульса (2.1). В нем m1 и V1 - это, например, масса и скорость пули, а m2 и V2 - соответственно масса винтовки и скорость отдачи, приобретаемой винтовкой при выстреле. Это же уравнение (2.1) описывает и закон сохранения импульса вагона, свободно катящегося по рельсам под мостом, с которого в вагон насыпают песок. Если до моста масса вагона была та скорость V1, то после моста масса вагона с песком возрастает до m2. При этом импульс вагона Р остаётся неизменным.
То же самое справедливо и при движении тела во времени. Только теперь не скорость движения является функцией от массы движущегося тела, как было в примере с вагоном, а наоборот: величина массы тела зависит от скорости у движения данного, тела во времени. Это и отражает уравнение (2.2) и получаемая из него простым алгебраическим преобразованием известная в СТО формула для релятивистской массы
(2.3)
Из (2.3) понятно, что масса тела возрастаете увеличением скорости У его движения в пространстве. (Так как
. СТО объясняет, что это увеличение массы тела вызывается тем, что в массу превращается кинетическая энергия, сообщаемая телу при его ускорении. А вот из теории движения не только понятна причина возрастания массы, но и объясняется закон, по которому происходит это увеличение массы. Оно обусловлено действием закона сохранения количества движения тела во времени. Это один из важнейших законов природы наряду с хорошо всем известным законом сохранения обычного импульса.
Вооружившись законом сохранения-количества движения во времени, мы теперь можем приступить к реализации мечты Е. Л. Фейнберга о выводе основных уравнений формул СТО исходя из динамических характеристик движения тел. Посмотрим, например, что происходит с размерами тел при их движении в пространстве-времени. Для этого домножим обе части уравнения (2.2) на некоторую длину l0, измеренную вдоль направления движения тела в пространстве. Этим мы превратим данное уравнение в уравнение для закона сохранения момента количества движения тела во времени:
(2.4)
Обозначим произведение lоу в уравнении (2.4) как некую новую длину l, а величину m заменим её значением m0lу из формулы (2.3). Тогда уравнение (2.4) превратится в тождество, и мы тем самым докажем известную формулу СТО для лоренцева сокращения длин при движении тел:
(2/5)
Если же мы возьмем отрезок l0 не вдоль, а перпендикулярно направлению движения тела в пространстве, то векторное произведение l0 на mу будет равно нулю при любых значениях у (как векторное произведение параллельных векторов).
Поэтому в последнем случае l1 = l0 при любых у. То есть размеры тел в направлениях, перпендикулярных направлению их движения в пространстве, остаются неизменными при любых скоростях движения.
Ну а формулу СТО для релятивистского замедления хода времени на движущихся телах
(2.6)
Разберем теперь, что такое преобразования Лоренца, о которых уже упоминалось выше. Когда вы едете в поезде и находитесь на расстоянии X' от задней стенки последнего вагона, то расстояние от Вас до станции, от которой отъехал поезд, составляет:
(2.7)
В конце XIX века результаты опыта Майкельсона указали, что свет от фар едущего паровоза летит вперед относительно паровоза с такой же скоростью, с какой он летит, в тот же момент и относительно столба на обочине дороги. Это открытие потрясло физиков. Начались поиски таких преобразований координат, которые оставляли бы скорость света С неизменной при переходе от движущейся к неподвижной системе отсчёта. Они были найдены в 1904 г. X. Лоренцем.
Поскольку мы уже знаем, как зависят длина тела и ход времени на нем от скорости движения тела в пространстве, то для нас уже не составит особого труда вывести: формулы преобразований Лоренца.
Для едущего в поезде наблюдателя кажется, что это не поезд едет, а окрестным поля и леса движутся относительно него в обратную сторону со скоростью - U. Поэтому расстояния Х до станции (отмеченные верстовыми столбами вдоль дороги) на движущейся относительно него земле подвергаются лоренцевому сокращению по формуле (2.5) и становятся для него равным Х' = Ху, где
- скорость движения поезда во времени. Тогда вышеприведенное выражение для преобразования Галилея (2.7) превращается в формулу преобразования Лоренца, для пространственных координат:
(2.8)
получим:
(2.9)
- время, измеряемое собственными часами пассажира поезда, а t -время, измеряемое часами на станции. Понятно, что, когда поезд был еще на станции (Х= 0), показания обоих часов совпадали.
Ну и, наконец, выведем формулу сложения скоростей СТО, которая даст ответ на вопрос, почему столь странные результаты получились в опыте Майкельсона и в; опытах Физо. Когда пассажир поезда шагает вперед по ходу поезда со скоростью V' относительно вагона, то расстояние X' пройденное пассажиром в вагоне за собственное время т, измеренное часами в вагоне, составит величину X'= 1/
. Подставим это выражение вместо X' в формулы (2.8) и (2.9), а затем разделим (2.8) на (2 9) В результате получим формулу для суммарной скорости движения пассажира относительно земли, по которой едет поезд:
(2.10)
Начав этот раздел с разговора о количестве движения во времени, давайте и закончим его разговором об этом мнимом импульсе mу. Домножив обе части уравнения (1.16) на m2с2(m квадрат с квадрат) и вспомнив, что mу = m0у0, получим выражение:
(2.11)
А домножив почленно обе части уравнения (2.11) на С2(c квадрат), получим известное в СТО уравнение:
(2.12)
Эти формулы скоро понадобятся нам. А отсылать читателя за ними к учебникам по СТО мы постеснялись, ибо тогда ему пришлось бы "перелопатить" десятки страниц, и неизвестно еще, с каким результатом. Наш же вывод с помощью теории движения во времени занял всего несколько страниц. Надеемся, что преподаватели физики с Удовольствием возьмут его на вооружение. Это позволит им и их слушателям экономить немало времени даже без "машины времени", к изобретению которой (чем черт не шутит!) может привести дальнейшая разработка теории движения во времени.
Для понимания дальнейшего в теории движения и вихревой энергетике нэп понадобится одна очень важная формула. А именно - знаменитая формуя Эйнштейна, связывающая массу с энергией Е = mС2(c квадрат). До Эйнштейна в классической механике полагали, что кинетическая энергия движения тела в пространств) определяется формулой
(2.13)
импульс Р - это произведение массы тела на его скорость, а скорость фотонов света: С, то в данном случае Р = mС. Отсюда следовало для фотонов:
(2.14)
(1.15)
Расчёты по формуле (2.15) показывали, что в каждом грамме любого веществ содержится столько внутренней энергии, что если бы её высвободить и превратить электроэнергию, то хватило бы на год отапливать и освещать целый город. Но в начале XX века никто не знал, как высвободить эту энергию. Лишь последующее развитии ядерной физики, физики элементарных частиц и ядерной энергетики с высоко точностью подтвердило догадку Эйнштейна и правильность формулы (2.15).
Но никто до сих пор не мог объяснить, что это за "энергия покоя" и откуда он берётся. Да и строгого вывода формулы (2.15) не существовало. Сам Эйнштейн при ее выводе в [16] использовал методы приближенного исчисления, дающие заведомо не очень точные результаты. А последователи гения, угадавшего эту формулу, по примеру В. Паули пытались найти точный вывод ее с помощью интегрального исчисления. В некоторых справочниках (например, в [17]) до сих пор фигурирую этот "вывод":
(2.16)
. Дифференциалы в нем означают пределы бесконечно малых величин ?Р и ?l при ?t, стремящемся к нулю. Но соотношение неопределенностей квантовой механики, открытое В. Гейзенбергом пять лет спустя после публик В Паули вышеприведенного "вывода" формулы Эйнштейна, гласит, что произвел не может быть меньше величины постоянной Планка h. Значит, в (2.16] знаком интеграла
. И при
это выражение стремится к бесконечности вместо ожидаемой бесконечно малой величины С2(c квадрат)dm. Так квант механика зачеркнула труд разработчиков теории относительности, пользовавшихся классической механикой с ее бесконечно малыми величинами. Остается то удивляться составителям современных справочников.
Но ценность формулы Эйнштейна от этого не уменьшается, она блестяще подтверждается работой атомных электростанций, в которых высвобождает используется часть энергии покоя урана.
Современный французский критик теории относительности Л. Бриллюэн отмечал, что формулу Эйнштейна
"невозможно вывести ни из одной, существующей в настоящее время теории или модели", как и формулу М. Планка
. Он писал, что эти угаданные двумя гениями формулы - "не результат исходного пункта нашего мышления", что смысл "троицы", энергия = масса на скорость в квадрате, составляющей итог всех законов физики, всё ещё находится в глубокой тайне".
В книге [8] указан ещё один возможный ответ на вопрос о том, что такое энергия покоя тела. Из закона всемирного тяготения Ньютона вытекает, что всякое тело со; вокруг себя гравитационное поле (поле тяготения), каждая точка которого характеризуется потенциалом
(2.17)
Энергия гравитационного взаимодействия
(2.18)
кг, составляет -6-106(десять в шестой степени). Чтобы поднять яблоко и забросить его в дальний космос, где притяжение Земли уже исчезающе мало, надо совершить положительную работу 6-106(десять в шестой степени) Дж. Сумма этой положительной энергии и найденной выше отрицательной энергии связи и даст почти нулевую энергию связи яблока с Землей в дальнем космосе.
В этом примере мы учли притяжение яблока только к Земле. Но на него действ еще и поля тяготения от Луны, Солнца и других бесчисленных тел Вселенной Попробуем вычислить суммарный гравитационный потенциал, создаваемый всеми ими, а затем и суммарную энергию гравитационной связи нашего яблока со всеми телами Вселенной. На первый взгляд эта задача может показаться немыслимой, ибо Вселенная безгранична, а расстояния до небесных тел так велики...
Но по современным представлениям Вселенная имеет конечный объём, определяется радиусом кривизны её пространства (или, для краткости, прорадиусом Вселенной)
. В этом объеме довольно равномерно распределены галактики, составляющие массу Вселенной
г. Величины
хоть и не очень точно, но уже вычислены астрофизиками по результатам многочисленных наблюдений. А согласно космологическому принципу Эйнштейна все точки Вселенной равноценны. Поэтому любую из них можно рассматривать находящуюся на расстоянии R0 от "центра массы" Вселенной. Тогда гравитационный потенциал, создаваемый всей массой Вселенной в точке, где находится наше яблоко (как и в любой другой точке), будет как на поверхности шара с радиусом и массой Вселенной и составит величину
(2.19)
0 приблизительно равен квадрату скорости света -С2(с квадрат), но со знаком минус. (Гравитационный потенциал имеет размерность квадрата скорости.)
Вычислим теперь энергию гравитационной связи тела со всеми остальные телами Вселенной как произведение массы этого тела на гравитационный потенциал Вселенной:
(2.20)
Видим, что с этой точки зрения величина -С2(с квадрат) в формуле Эйнштейна - это просто квадрат скорости света, а гравитационный потенциал Вселенной.
Приблизительное, а не строгое равенство мы получили потому, что не очень-то знаем величины
. Но строгое равенство не доказано ни в одном известном выводе формулы Эйнштейна. Не исключено, что за неточностью этого равенства кроется будущая фундаментальная теория, развивающая далее теорию относительности. Ведь и казавшаяся в прошлом столь точной механика Ньютона тоже, как оказалось, давала только приблизительные значения вычисляемых величин. За этой неточностью скрывалась релятивистская механика, без которой невозможно решать такие, например, задачи, как движение частиц в ускорителях, где скорости приближаются к скорости света С.
Полученная формула (2.20) отличается от эйнштейновской ещё и знаком минус, потому что энергия гравитационной связи считается отрицательной. На это можно было бы сказать, что знак - дело условное, и напомнить, что на самом деле отрицательных энергий не бывает, как и отрицательных масс. Что отрицательная энергия связи в системе из нескольких тел, например в атоме, - это всего лишь недостача положительной массы-энергии до какой-то большей величины. А в целом сумма всех энергий системы остается положительной величиной. Но в следующих разделах книги мы найдем более интересный ответ на этот вопрос об отрицательных
энергиях.
А здесь ещё раз отметим, что как висящее на дереве яблоко обладает потенциальной энергией, которая высвобождается при падении яблока на землю так и все "висящие" в пространстве Вселенной тела тоже обладают такого же рода потенциальной энергией
. Но только они не могут "упасть" к "центру Вселенной", как не падает на планету её спутник.
2 принимала значения, большие скорости света С. Это получилось потому, что величин расстояний l и времени
при этом брали из разных систем отсчета, что некорректно
Но именно так экипажам космических межзвездных кораблей в будущем удобнее всего будет выражать и измерять "собственную скорость" корабля:
(2.21)
А вычисляя импульс своего корабля, его экипаж будет просто умножать масса покоя корабля m0 на "собственную скорость":
(2.22)
при преобразованиях Лоренца, так же, как считается инвариантным собственное время.
Получаемая по (2.22) величина импульса соответствует релятивистскому импульсу корабля, вычисляемому земным наблюдателем по формуле Р = mV, в которой m = m0/y релятивистская масса корабля.
По аналогии с существующим в СТО выражением "энергия покоя" тела назовем величину "
(2.23)
В формулах (2.21) и (2.22) появился любопытный сомножитель - отношение ß/y на который обращалось внимание еще в книге [8]. Это отношение означает безразмерную собственную скорость тела
(2.24)
3 (ей соответствует скорость движения в пространстве
. В [8] обнаружены и
перегиба на графиках еще двух функций (при
и при у ~ 0.933)
наибольшую важность для нас имеет, конечно же, приведенная здесь кривая зависимости импульса тела Р от скорости у движения этого тела во времени.
Эйнштейновское утверждение о равноправии всех скоростей предполагало отсутствие особых точек на графиках зависимостей энергии и импульса тела от его скорости. Но никому не приходило в голову строить графики зависимостей величин от какого-то "фактора Лоренца", как называли величину
2 (бетта в квадрате)
догадываясь, что она означает скорость движения тела во времени.
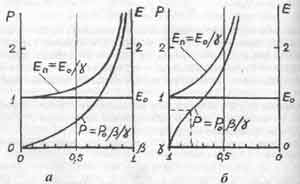
Рис. 2.1
Отмеченные выше скорости, соответствующие точкам перегиба графиков, можно назвать особыми скоростями движения. Следует согласиться, что скорость с вакууме С - тоже особая скорость, можно сказать, самая особая, мировая коне Следующая за ней по важности - особая скорость
, которая в [8] названа "первой космической скоростью Вселенной" в предложении, что с такой скор движутся наиболее отдаленные от нас галактики, и что именно с такой скор движется относительно "центра масс Вселенной" каждое ее тело. При этой скорости ß = у и потому достигается равнораспределение энергий движения в пространстве и во времени и наблюдается ряд экстремумов на графиках, строившихся в [8].
Называя указанные скорости движений особыми, мы, казалось бы, замахиваемся на то, что ещё недавно считалось святая святых современной физики - постулаты Эйнштейна. Но ведь найденные точки перегибов и экстремумов существуют! От этого факта уже не отмахнуться, как не отмахнуться и от наличия во Вселенной выдел (абсолютной) системы отсчета, связанной с реликтовым излучением. Остается только выяснить, в каких процессах проявляются эти особые скорости.
Кстати, с особой скоростью
мы имеем дело повседневно: т минимальная скорость распространения света (электромагнитных волн) в воде. Случайно ли? Ведь вода хранит в себе столько тайн и обладает столь удивительными аномальными свойствами, отличающими её от других веществ. А совпадения природе редко бывают случайными.
(2.25)
- вектор ускорения, возникающего под действием внешней силы
.
Эта формула написана на основании третьего закона Ньютона: действие противодействию. Но в справочниках Вы вряд ли найдете ее. Объясним почему. В данном случае сила инерции противодействует внешней силе F, вызывающей ускорение тела в пространстве, описываемое вторым законом Ньютона:
(2.26)
Со времен Э. Маха бытует мнение, что силы инерции обусловлены гравитационным взаимодействием тела со всеми остальными телами Вселенной. Но почему тогда проявляются мгновенно? Ведь до остальных тел Вселенной так далеко, а теория относительности утверждает, что взаимодействие не может передаваться мгновенно! Этот вопрос тоже остаётся без ответа и мучает физиков. Силы инерции - одна из самых больших загадок физики. Не сумев объяснить их, физики в последние десятилетия начали даже изгонять упоминания об этих силах со страниц учебнике Так, например, бытовавшее ранее выражение "центробежные силы" (они являют одним из проявлений сил инерции) напрочь исчезло из литературы. Вместо это теперь говорят о противодействующих центробежным центростремительных силе описываемых формулой (2.26), забывая, что у всякой силы всегда имеется противодействующая ей.
В [9] было сделано предположение, что гравитоны являются тахионами, а любые гравитационные взаимодействия могут распространяться почти мгновенно на любые расстояния. Это возвращает нас на позиции принципа дальнодействия сил гравитации, выдвинутого И. Ньютоном. Кроме того, это объясняет мгновенное проявления сил инерции как результата гравитационного взаимодействия тела ? всеми остальными телами Вселенной.
В [8] с помощью теории движения во времени выведена формула (2.25) исходя из (2.26), т.е. сделано то, что до сих пор не удавалось поколениям механиков. Для это было вычислено ускорение движения тела во времени как производная по dt от y.
(2.27)
Но, как следует из формулы (2.27), ускорение движения во времени зависит еще и от параметра ß/y, названного нами безразмерной собственной скоростью движения тела. Этот параметр возрастает с ростом скорости V движения тела в пространств. Следовательно, ускорение движения тела во времени должно возрастать по абсолютной величине с ростом скорости движения этого тела в пространстве. Последнее обстоятельство совершенно непривычно для людей, привыкших иметь дело с классической механикой.
Если выражение (2.27) домножить на массу тела m, то получается выражение для силы, аналогичное формуле (2.25):
(2.28)
Полученное выражение (2.28), имея требуемый знак минуса, удивительно похоже на выражение (2.25) для сил инерции. Только малопонятный параметр ß/y мешает полному совпадению формул. Но если в формуле (2.28) величину ускорения V не связывать с величиной параметра ?/?, то есть считать независимой от него (или считать отношение ß/y постоянно равным единице), тогда формула (2.28) превратится в формулу (2.25) для сил инерции!
Но разве возможно, чтобы тело ускорялось, а отношение ß/y оставалось неизменным? Разве бывает так, что тело ускоряется, а абсолютная величина скорости его движения не изменяется? Оказывается, бывает. Так, центростремительное ускорение, перпендикулярное тангенциальной скорости Vr движения тела по круговой траектории, не изменяет абсолютную величину этой скорости.
В [8] сделано предположение, что фигурирующие в выражении (2.28) величины ? и ? относятся не к локальному движению тела под действием ускоряющих его локальных внешних сил, а к вселенскому движению вещества в гравитационного замкнутой Вселенной вокруг ее "центра масс", аналогичному движению спутника Земли по круговой орбите. Только если первая космическая скорость у поверхности Земли составляет 7,9-103(10 в третей степени) м/сек, то "первая космическая скорость" для всей Вселенной, имеющей массу ~1055 г и радиус ~1028 см, должна составлять C/V2 . Именно при такой скорости тела ß/y. Это та самая особая скорость, на которую мы уже обратили внимание выше.
Остается только допустить, что локальные ускорения тел под действием тех или иных локальных сил не изменяют абсолютной величины скорости "орбитального" движения этих тел относительно "центра масс" Вселенной, а только изменяют ее направление. Но в разделе 1.3 мы уже видели, что изменение скорости движения тела в пространстве не изменяет абсолютной величины |C| комплексной скорости J движения тел. Следовательно, при переходе к космологическим масштабам надо говорить уже не о движении в пространстве, а о движении в пространстве-времени, как на это давно указывает теория относительности.
Таким образом, можно полагать, что в формуле (2.28) отношением ß/y характеризует не локальные движения тел, а движения вещества Вселенной в целом по круговой траектории. И можно говорить, что силы инерции действительно зависят от движения вещества Вселенной в целом, но возникают как силы ускорения движения тела во времени.
Выводы к главе
2. Вывод остальных основных формул специальной теории относительности в теории движения столь же прост, нагляден и понятен.
З. Энергия покоя тела, которую называют еще внутренней энергией тела, выражаемая формулой Эйнштейна E0 = m0C2(с квадрат), численно совпадает с энергией гравитационной связи данного тела со всеми остальными телами Вселенной. При этом квадрат скорости света С2(с квадрат) равен гравитационному потенциалу Вселенной, взятому с противоположным знаком.
4. График зависимости импульса тела от скорости движения его во времени у имеет точку перегиба при
, которой соответствует скорость движения в пространстве
. Скорость
- тоже особая скорость движения. При ней
5. Силы инерции - это силы ускорения движения тела во времени при замедлении его движения в пространстве. С другой сторон, силы инерции - это силы взаимодействия тела со всеми телами Вселенной. Мгновенность проявления сил инерции объясняется мгновенностью распространения во Вселенной переносчиков этих сил - гравитонов, являющихся разновидностью тахионов.
ЭНЕРГИЯ В ТЕОРИИ ДВИЖЕНИЯ
Условившись применять по мере возможности законы обычной механики к движению тел во времени, подумаем теперь над тем, может ли существовать энергия движения тела во времени Ет. Мы уже поняли, что покоящееся в пространстве тело движется во времени с наибольшей мнимой скоростью у0= 1. Следовательно, оно в состоянии покоя будет обладать максимальной энергией движения во времени если последняя существует. Интересно, как будет соотноситься эта энергия с энергией покоя тела Ео? А с полной энергией тела Еп?
В СТО полная энергия движущегося тела определяется формулой Эйнштейна Еп = mС2(с квадрат). Подставляя сюда значения m из (2.3) и учитывая (2.15), получают
(3.1)
В учебниках часто приводят график зависимости
который мы воспроизводим на рисунке 3.1. Справедливо полагают, что полная энергия складывается из энергии покоя тела E0 = m0C2(с квадрат) и кинетической энергии Ек, которую тело получает от движения, ускоряющего данное тело до скорости V. То есть
(3.2)
(3.3)
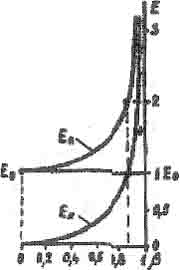
Рис (3.1)
Но сначала определим точнее это понятие. Для этого умножим обе части уравнения (1.16) на
Еп=mС2 (с квадрат).Получим:
(3.4)
(3.5)
(3.6)
На рисунке 3.2 приведены графики этих энергий как функции от скоро движения тела во времени у, величина которой отложена на оси абсцисс в линейном масштабе, а величина ß - в нелинейном (на рис. 3.1. в линейном масштабе вкладывали, наоборот, величину ß ). Надо сказать, что при переходе от линейной к нелинейной шкале оси абсцисс картина хода кривых изменяется, хотя все координаты их точек остаются теми же.
Рис.(3.2)
Видим, что с уменьшением скорости движения тела во времени энергия его движения во времен уменьшается линейно. При этом покоящемуся в пространстве телу соответствует Ет = E0, Ev = 0. Значит энергия покоя тела Е0 - это энергия движения во времени тела покоящегося в пространстве.
Поколения физиков лом головы над вопросом, что такое таинственная "энергия покоя" тела, понятие о которой ввел Эйнштейн не расшифровав это понятие. И мы с вами наконец выяснили, что такое. Вы спросите, что тогда такое потенциальная энергия тела в гравитационном поле Вселенной которой велась речь в предыдущем разделе? Но ничто не запрещает, чтобы это была одна и та же энергия.
Дуализм!
Рассматривая рис. 3.2, замечаем, что если энергия движения тела в пространстве может расти неограниченно с увеличением ß то энергия его движения во времени не превышает величину Е0. Но поначалу, при
, она больше энергии движения в пространстве. Такое поведение энергии определяется неукоснительным соблюдением закона сохранения количества движения тела во времени, о котором мы говорили в разделе 2.1.
Может, скорость движения
потому и является особой скоростью, что при ней достигается не только равенство скоростей движения тела в пространстве и во времени y, но и равенство энергий этих движений. То есть достигается равнораспределение энергий движения в пространстве и во времени.
Эйнштейн, показав, что энергия покоя тела Е0 инвариантна при преобразованиях Лоренца, отождествлял ее с внутренней энергией этого тела. Мы же всё более убеждаемся, что эти два термина обозначают разные понятия, что под внутренней энергией тела следует понимать энергию движения данного тела во времени Ет, которая уменьшается с ростом скорости V движения тела, а потому далеко не инвариантна, в отличие от Е0.
Хотя с увеличением скорости V движения тела в пространстве энергия его движения во времени Ет уменьшается, полная (релятивистская) энергия Еп этого тела растёт в соответствии с (3.1). Следовательно, при замедлении движения тела во времени разность энергий
(3.7)
(3.8)
(3.9)
Если при замедлении движения тела во времени часть энергии этого мнимого движения превращается в энергию движения в пространстве, то возникает вопрос: а нельзя ли найти такие условия, при которых эту энергию, бывшую до того частью "энергии покоя" тела, можно было бы использовать в полезных целях, например высвечивая ее в виде излучения, а затем превращая в электроэнергию. Ведь это огромная энергия! Из каждого грамма вещества - "топлива" - ее могло бы выделяться в тысячи раз больше, чем выделяется из грамма урана в ядерном реакторе. Это было бы самое калорийное "топливо"! В таком процессе масса непосредственно превращалась бы в энергию, а "топливом" могло бы служить любое вещество.
Ведь атомы любого вещества - это словно консервы со сгустками энергии. Но туристы хорошо знают, что можно умереть от голода на мешке с запаянными консервными банками, если не иметь ключа для их открывания. Таковым "ключом" для высвобождения внутренней энергии вещества до последнего времени считались только ядерные реакции, протекающие, например, в реакторах атомных электростанций и в атомной и водородной бомбах. Но и там для эффективного протекания процесса требуется создавать особые условия (критические массы, сверхвысокие температуры). Да и опасны эти источники энергии. А потому дорогие и в конечном счете низкоэффективные. Поэтому надо продолжать поиски других "ключей" для высвобождения внутренней энергии вещества.
Из вышеизложенного понятно, что для высвобождения внутренней энергии вещества необходимо прежде всего замедлять движение его во времени, ускоряя движение в пространстве. А для этого необходимо привносить извне кинетическую энергию, притом большую той, которая выделяется. Процесс на первый взгляд может показаться энергетически невыгодным. Но только на первый взгляд. Ведь и для получения энергии от сжигания угля необходимо сперва разогреть уголь до воспламенения. Вложенная извне энергия не исчезает, а остается в системе, при этом выделяющаяся энергия, которую мы хотели бы использовать, добавляется к ней. Посмотрите: кривая графика для Еv на рис. 3.2 лежит выше кривой Eк. Расстояние между ними и есть выигрыш в энергии. Он появляется уже при значениях у, близких к 1. Это значит, что не до такой уж большой температуры надо разогревать наше "топливо", чтобы получить ощутимый выход энергии. Может, даже температуры топки паровоза хватило бы, чтобы разогнать молекулы "топлива" до необходимых скоростей теплового движения?
Конечно, для этого надо знать, в каком именно веществе наиболее легко может пойти такой процесс высвечивания внутренней энергии, и надо знать, при каких условиях он может идти наиболее эффективно. Ведь и обыкновенный уголь в обыкновенной топке не при любых условиях загорается.
И только ли ускорением в пространстве можно тормозить движение тела во времени? Может, существуют более рациональные методы? Ведь мы только-только осваиваем азы теории движения во времени, которая находится еще в зачаточном состоянии!
Похоже, что в природе существуют мощные источники энергии, освобождающейся при замедлении движения тел во времени. Это не только "черные дыры", в которых определённо идёт этот процесс. Думается, что он идёт и в недрах Солнца, может быть, даже и в недрах Земли в какой-то степени. Ведь давно известно, что в ней существуют какие-то неучтённые источники энергии.
До последнего времени источником энергии излучения Солнца считались реакции термоядерного синтеза, идущие в его недрах. Но они должны были сопровождаться выделением огромного количества нейтрино - всепроникающих безмассовых частиц, движущихся, как до сих пор считают почти все физики, со скоростью света С. (В книге [9] выдвинута гипотеза, что нейтрино летят со сверхсветовыми скоростями.) В 60-е годы сначала в США, а затем в СССР построили большие установки для регистрации солнечных нейтрино, но оказалось, что их поток по крайней мере в 3 раза ниже ожидавшегося. С тех пор учёные теряются в догадках.
Так, может быть, действительно основным источником энергии Солнца являются не термоядерные реакции, а просто разогретое вещество высвечивает часть энергии движения во времени?
Но для этого ей надо каким-то образом превратиться не в энергию движения в пространстве Ev, а в кинетическую энергию атомов Ек. Последняя, как мы уже видели, не идентична Ev, а является её составной частью.
В СТО кинетической энергией E. называют энергию, определяемую формулой (3.3). Не будем ломать эту традицию, хотя член-корреспондент PAEH "нерелятивист" В. M. Мигунов [18], а вслед за ним академик АЭН РФ Г. E. Иванченко [19],тоже пришедший к выводу об уменьшении внутренней энергии элементарных частиц с увеличением скорости их движения в пространстве, утверждают, что кинетической энергией тела следует называть разность энергий Ед, определяемую выражением (3.7).
Они уверяют, что энергия Ек, сообщаемая телу от движителя при ускорении движения тела в пространстве и называемая в СТО кинетической энергией, на самом деле затрачивается на деформацию пространства-времени (или эфира), в котором движется тело. При этом Мигунов пишет, что энергия Eк идёт на изменение гравитационной связи частицы со Вселенной и перераспределяется во Вселенной, со всеми телами которой частица находится в "динамическом равновесии" [18].
А у движущейся частицы, уверяет Иванченко, всегда остаётся только суммарная масса-энергия Е0 = Ет + Е?, которая, по его мнению, инвариантна. Напомним, что в СТО тоже считают энергию покоя тела Eо, инвариантом, не зависящим от скорости движения тела. Если бы это было действительно так, то на этом можно было бы закончить нашу книгу, так как это закрывало бы возможность превращения части массы покоя вещества в энергию излучения. Но, к счастью, это не совсем так, точнее, не всегда так, в чем мы убедимся в четвертой главе.
В книге [8] далеко не впервые было написано столь необычное для специалистов по теории относительности уравнение, получаемое из (3.4):
(3.10)
(3.11)
(3.12)
(3.13)
Сам M. Планк выводил формулы (3.13) довольно сложным путем, приведенным например, в [21, 22] и основанном на предварительном доказательстве инвариантности давления газа и энтропии при преобразованиях Лоренца.
Необходимость возврата теоретиков в 60-е годы к широкому обсуждению форм (3.13), 50 лет не вызывавших сомнения у физиков, была обусловлена тем, что в 191 году появилась посмертная публикация Г. Отта [23], в которой обращалось внимание на то, что в некоторых случаях формулы (3.13) ведут к парадоксальным результата! и предлагалось заменить их формулами.
(3.14)
Дискуссия теоретиков продолжалась несколько лет, пока Луи де Бройль уравнением (3.11) не показал, что результаты Планка-Лауэ и Отта не противоречат друг - другу, а просто авторы разговаривают на разных языках. Ибо член
в уравнении (3.11), совпадающий с формулой Планка-Лауэ (3.13), утверждал де Бройль, описывает переносимую телом при его движении тепловую энергию, а член
описывает "Энергию переноса" этой тепловой энергии (или просто тепла) из одной инерциальной системы отсчета в другую.
К сказанному остается только добавить, что тепловая энергия газа в баллоне - это ведь часть внутренней энергии, содержащейся в баллоне, она является добавкой энергии покоя молекул, находящихся в баллоне. Поэтому формула (3.13) для тепло газа совпадает с нашей формулой (3.6) для внутренней энергии тела или энергии его движения во времени.
А то, что де Бройль назвал "энергией переноса", является не чем иным, как определяемой формулой (3.5) энергией движения в пространстве.
Таким образом, и де Бройль, и мы пришли разными путями к одному и тому же результату. Только великий французский физик на том и остановился в данном вопросе, рассматривая уравнение (3.11) лишь как вспомогательное.
И вообще участники той дискуссии 60-х годов считали, что рассматриваемые ими вопросы имеют исключительно теоретическое значение и далеки от насущных потребностей людей. Так, советский участник той дискуссии В.А. Угаров в [22] писал: " ... формулы (3.13) имеют скорее принципиальное, чем практическое значение".
Такая убежденность основывалась на том, что при доступных людям технических скоростях движения макроскопических тел (например, баллонов с газом) релятивистский фактор ß = V/C чрезвычайно мал, а потому значения Q и Т, вычисляемые по формулам (3.13), оказывались практически неотличимыми от значений Q0 и Т0 даже при космических скоростях (V ~ 104 (10 в четвертой степени) м/с) движения тел.
Эксперимент, настоящий эксперимент, в большинстве случаев идет впереди теории, которой остается только объяснить его результаты. Так произошло и в случае, описанном в 1989 году немецким журналом "Пространство и время" [24]. Студент-энергетик Людвиг Гербранд в 1930 году был направлен на преддипломную практику на гидроэлектростанцию Рейнфельден, где монтировали новый электрогенератор взамен износившегося. На этой электростанции, построенной еще в конце XIX века, не было высокой плотины, а просто часть потока реки Рейн отводилась дамбой к турбогенераторному залу. Студент обратил внимание на то, что турбогенераторы, пропуская через себя всего 50 куб. м воды в сек., производят электроэнергии столь же много, как на соседней новой гидроэлектростанции в Рыбурге, имеющей высоту напора воды 12 м, вырабатывают огромные турбогенераторы с пропускной способностью 250 куб. м в сек.
Заинтересовавшись этим парадоксальным фактом, Гербранд понял, что причина - в динамическом напоре потока воды, подводимой к турбине.
Перегораживая реку высокой плотиной, проектировщики стремятся создать как можно больший гидростатический напор воды. При перепаде уровней воды H гидростатическая (гравитационная) энергия, запасенная водой за плотиной, составляет
(3.15)
(3.16)
(3.17)
А вот на старой электростанции не было высокой плотины, зато дамба захватывала самую быструю часть течения реки и по сужающемуся каналу подводила его прямо к турбинам. При этом в сужающемся канале скорость потока, подаваемого на лопатки турбины, ещё возрастала и оказывалась гораздо большей, чем на новой электростанции с ее высокой плотиной. А кинетическая энергия потока, согласно формуле (3.16), является квадратичной функцией от его скорости! Если скорость потока в 2 раза больше, то энергии вырабатывается в 4 раза больше при одном и том же расходе воды.
Но в действительности турбогенераторы старой электростанции вырабатывали электроэнергии еще больше, чем показали студенту эти простые расчёты. Откуда она берется? Обеспокоенный студент пишет письмо своему научному руководителю профессору Финзи. Тот ответил следующее: "Не волнуйтесь. Генератор работает без проблем... Мы инженеры-электрики. Поэтому остальные вопросы не наши, чтобы их решать. Оставьте их гидравликам...".
У немцев уже тогда торжествовал узкопрофессиональный подход к делу.
Увы, скоро Гербранда призвали в армию, а потом война не позволила ему заниматься гидроэнергетикой. Только в 70-е годы он возвратился к своим студенческим вычислениям. Пытается взять патент на способ повышения энергетического выхода гидроэлектростанций, но получает отказ со ссылкой на то, что его предложения нарушают закон сохранения энергии. Обращается к правительству и промышленникам - без успеха. Дымовая завеса вульгарно понимаемого закона сохранения энергии мешает им признать факты.
Попробуем дать объяснения эффекту, подмеченному Гербрандом, с позиций теории движения. Она утверждает, что при ускорении движения тела в пространстве часть его внутренней энергии превращается в энергию движения тела в пространстве EV2(v в квадрате) названной де Бройлем "энергией переноса", и суммируется с кинетической энергией Ек, привносимой извне. Правда, такое превращение напоминает перекладывание денег из левого кармана в правый: от этого человек не становится богаче. Но не надо забывать, что внутренняя энергия - это не только энергия покоя атомов, составляющих тело, но и плюс к этому еще и энергия их теплового движения в теле. Однако при земных скоростях движения тел изменение величины тепловой энергии Q, как показывали формулы (3.13), должно быть весьма незначительным. Но...
Но формулы (3.13) выведены для баллона с газом, а ведь вода - это не газ, состоящий из отдельных не связанных друг с другом и почти свободно движущихся в пространстве и соударяющихся друг с другом молекул. Вода ведь имеет межмолекулярные связи, обеспечивающие ее монолитность и целостность как единого квантового механизма. Вода - хоть и текущее, но цельное тело, а не рой молекул! Поэтому можно предположить, что когда мы ускоряем движение воды как целого тела, то требуемое теорией движения превращение части массы-энергии покоя воды и части ее тепловой энергии в энергию движения в пространстве Еv происходит не по отдельности, а вместе, ибо вместе они и составляют внутреннюю энергию воды.
А дальше остается только допустить, что тепловой энергии колебаний молекул легче превращаться в энергию движения в пространстве, нежели внутренней энергии атомов, составляющей основную часть энергии покоя воды. И происходит то, чего никак не ожидали теоретики, обсуждавшие в 60-е годы формулы Планка-Лауэ: в ускоряемом потоке воды происходит ее самопроизвольное охлаждение с превращением части запасенной в воде тепловой энергии в энергию движения потока в пространстве. Масса покоя воды m0 при этом остается неизменной: вода как бы "откупается" от совершаемого над ней насилия (ускорения) "разменной монетой" -тепловой энергией, сохраняя неизменным число своих атомов и их массу-энергию
покоя.
При этом не нарушается закон сохранения энергии, хотя в результате поток воды приобретает скорость большую, чем ожидалось исходя из затрат только привнесенной извне энергии Ек. Но поскольку теплоемкость воды рекордно высока среди всех известных людям веществ, то даже при охлаждении всего на 10®С каждый литр воды может ускориться на 9 м/с. Представляете, какие огромные запасы только тепловой энергии содержатся в реках?!
Конечно, все это пока только робкая гипотеза, требующая додумываний и тщательной экспериментальной проверки. Но игра стоит свеч, хотя пока мало надежд, что всё это окажется столь просто и именно так. Ведь энергия движения в пространстве Ev, или "энергия переноса", как ее называл де Бройль, в которую превращается часть внутренней энергии тела при ускорении его прямолинейного поступательного движения, - это ещё не кинетическая энергия тела, а нечто иное. Да и с законом сохранения импульса тут мы, похоже, не всё согласовали.
Тем не менее, в предложениях Гербранда было ещё одно рациональное зерно, не отмеченное в [24]. Советские гидроэнергетики тоже подметили, что турбины с горизонтально расположенной осью, установленные, например, на Череповецкой ГЭС, вырабатывают энергии на 15- 20% больше, чем вертикальные турбины, имеющие такой же диаметр [25]. Это объясняют тем, что к горизонтальной турбине вода подается по прямому, а не изогнутому водоводу, и к гидростатическому напору воды, обусловленному перепадом высот ее уровней до и после плотины, добавляется еще и динамический напор течения реки, если оно не совсем "убито" плотиной.
Кроме того, работает эффект "гидравлического тарана": на лопатки турбины давит не только гидростатическая сила, создаваемая столбом воды высотой Н, но и сила инерции всей массы воды, движущейся в прямом водоводе и в примыкающей к нему части реки. Эта сила инерции больше гидростатической силы! С помощью "гидравлического тарана" мелиораторам при перепаде высот уровней воды всего в 1 м удаётся поднять воду по длинной трубе на высоту до 10 м [25].
1. Энергия движения тела во времени - это величина
. Она максимальна у покоящегося в пространстве тела, то есть когда у = 1. Из этого следует, что энергия покоя тела Ео - это энергия движения во времени тела, покоящегося в пространстве.
2. В теории относительности необоснованно и ошибочно отождествляют внутреннюю энергию тела с его энергией покоя Ео, которая инвариантна при преобразованиях Лоренца. Под внутренней энергией тела следует понимать энергию его движения во времени Ет которая не инвариант, а уменьшается с ростом скорости V движения тела в пространстве.
3. При ускорении поступательного движения тела часть его энергии покоя превращается в энергию переноса тела
, в состав которой входит еще и кинетическая энергия Eк, привносимая источником движущей силы, Но при поступательном движении тела наблюдатель может измерять только полную массу - энергию тела
, в состав которой аддитивно входят энергия движения тела во времени (внутренняя энергия тела Ет) и энергия переноса Ev.
4. Если бы удалось помешать разности между энергией покоя тела Ео и энергией движения его во времени Ет превращаться при ускорении тела в энергию переноса Еv а заставить эту разность энергий высвободиться, например излучиться, то это был бы неиссякаемый источник даровой энергии для человечества, ибо кинетическая энергия Ек, затраченная на ускорение тела, при этом не исчезает, а тоже может быть использована.
5. Понятие энергии переноса Ev ввел Л. де Бройль, рассматривая формулы Планка-Лауэ для релятивистского преобразования теплоты и температуры при переходе от одной инерциальной системы отсчета к другой. В них теплота, как внутренняя энергия газа в баллоне, тоже уменьшается с ростом скорости движения баллона в пространстве по такому же закону, как и энергия движения тела во времени в наших выкладках.
6. Практики-энергетики давно подметили, что в ускоряемом потоке воды происходит её самопроизвольное охлаждение с превращением части тепловой энергии воды в кинетическую энергию потока.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Мир животных не знаком с вращательным движением. Поэтому человечество в своём младенчестве ассоциировало движение в основном с поступательным перемещением в пространстве: ходьба человека, бег оленя, полёт птиц, стрелы, пули... Наконец, человек изобрел колесо (наконец потому, что американский континент до Колумба не знал колеса). Но кроме колеса да веретена люди много тысячелетий почти не использовали вращение. Даже астрономы пришли к мысли о вращении Земли лишь во времена Коперника и то через костры инквизиции. Только XX век, заменивший паровую машину с ее возвратно-поступательно движущимися поршнями на турбину и насадивший везде электромоторы, продемонстрировал возможности и преимущества вращательного движения.
Эйнштейн был дитя XIX века, хотя и дожил до середины XX. А в XIX веке всё ещё господствовали представления о том, что первичным является поступательное движение, а вращательному отводилась вспомогательная роль. Действительно: молекулы газа или пара до столкновения с поршнем движутся прямолинейно, поршень паровой машины тоже движется прямолинейно, и лишь колёса паровоза вращаются, чтобы сообщить поезду опять же поступательное движение по рельсам. Всё вокруг человека двигалось в основном поступательно и прямолинейно. Лишь планеты обращались вокруг Солнца. Но с ними имели дело только астрономы. Да и движение планет в первом приближении на небольших участках их орбит принимали за прямолинейное - уж слишком велики радиусы кривизны их орбит. Так поступал, например, А.Майкельсон в расчётах своего знаменитого опыта. Наверно, потому Эйнштейн не придавал особого значения вращательному движению и не уделил ему должного внимания в своих работах. Это было серьёзное упущение.
Ведь ещё великий Ньютон указывал, что вращательное движение, в отличие от относительного равномерного поступательного движения, абсолютно. Проявление абсолютности вращательного движения он усматривал в центробежных силах, возникающих при вращательном движении тел. Они всегда позволяют "не выходя из лаборатории" и без внешних ориентиров определить направление оси вращения и абсолютную скорость вращения. Именно абсолютность вращательного движения Ньютон считал подтверждением своих представлений об абсолютном пространстве и абсолютном времени. На особую роль вращательного движения указывал и Э. Мах, удивляясь тому, что силы инерции, проявляющиеся при вращательном движении к центробежные силы и обусловленные, по его мнению, влиянием далеких звезд, Действуют мгновенно, хотя до звезд так далеко...
Может, Эйнштейн потому и не любил говорить о вращательном движении, что казался от ньютоновских представлений об абсолютном пространстве и абсолютом времени? С другой стороны, вращательное движение с самого начала упорно не хотело укладываться в прокрустово ложе теории относительности, в чем мы убедимся в данной главе.
Теперь мы знаем, что круговое движение превалирует не только в звездном небе, но и в субатомном мире: электроны, согласно моделям Э. Резерфорда и Н. Бора обращаются вокруг ядра атома, а ядра тоже обладают моментом вращения. И вообще все элементарные частицы обладают спином - чем-то вроде внутреннего момента вращения. Даже фотон - частица того самого света, которому Эйнштейн уделил так много внимания, имеет спин 1h.
Но в познании законов вращательного движения мы по-прежнему проигрываем по сравнению с познанием прямолинейного движения, которого, по большому счёту, вообще не существует. Ибо прямая - это дуга окружности с бесконечным радиусом. А в природе, если верить теории относительности, не существует бесконечно больших расстояний. Самое большое расстояние равно радиусу кривизны Вселенной (или просто радиусу Вселенной) Rо. Потому прямая - это дуга с радиусом кривизны Вселенной R0.
Поступательное движение, как известно, - относительное. По крайней мере, так считают в СТО. А вот вращение - понятие абсолютное: если тело вращается, то этого свойства у него уже не отнять никакими преобразованиями координат. Ибо во вращающемся теле (или при вращении тела) возникают центробежные силы, а силы неустранимы ни при каких преобразованиях координат. Более того, как уже отмечалось в книге [8], силы, возникающие даже при мнимом движении тел, всегда являются реальными.
Релятивисты этого признавать не хотели. Им конечно же не нравились центробежные силы, напоминавшие об абсолютном пространстве и абсолютном движении в нем. А поскольку силы неустранимы никакими преобразованиями координат, то "релятивисты", недолго колеблясь, решили уничтожить их по-другому: объявили центробежные силы "кажущимися", обусловленными не физическими причинами, а изменением направления движения наблюдателя [26]. Получается, что испытуемому на центрифуге перегрузки только кажутся!
Но усилиями последователей Эйнштейна упоминания о центробежных силах постепенно исчезли из литературы и учебников по физике, где вместо них стали говорить только о противоположных им центростремительных силах, словно забывая о том, что у каждой силы имеется противодействующая ей.
Следует признать, что к концу XX века обозначился явный пробел в мировой науке в деле изучения вращательного движения. Пробел, приведший к тому, что человечеством упущено очень многое из того, что давно могло бы приносить ему огромную пользу.
В книге [9] показано, что "вертикальный запредельный мир" основной диаграммы теории движения, приведенной на рис. 1.1, описывает вращательное движение тел. Из диаграммы следует, что безразмерная тангенциальная скорость ßт вращательного движения не ограничена единицей (т.е. тангенциальная скорость V. вращения не ограничена величиной скорости света С), а может принимать и большие значения. Этот вывод, противоречащий постулату Эйнштейна, следует не только из диаграммы рисунка 1.1.
Такой вывод можно сделать и анализируя результаты известных экспериментов Ф. Гарриса (1913 г.) и Г. Саньяка (1914 г.), повторенных в 1925 г. А. Майкельсоном и А Гейлем, о которых рассказывается, например, в книге [27]. В их экспериментах луч света, поочередно отражаясь от зеркал, установленных по периметру вращающегося диска, облетал этот периметр как по вписанному многоугольнику и давал на экране интерференционную картину, складываясь с таким же лучом, облетающим диск в противоположном направлении.
В экспериментах выяснилось, что время t облета лучом диска при совпадении направления его полета с направлением вращения диска больше, чем когда свет летит навстречу направлению вращения диска. Притом ровно настолько, как если бы скорость света С суммировалась с тангенциальной скоростью Vт движения периферии диска, имеющего радиус R, по классической формуле сложения скоростей, то есть:
(4.1)
Этот результат, названный эффектом Саньяка, настолько в свое время ошарашил ученых, уже начавших свыкаться с утверждением Эйнштейна о том, что в природе не может существовать скоростей относительного движения, больших скорости света С, что... они предпочли не афишировать этот результат, не укладывающийся в прокрустово ложе теории относительности. Так, например, о нем ни слова не говорилось в претендовавшем на фундаментальность учебнике для вузов по оптике Г.С. Ландсберга [28], выдержавшем много переизданий.
И немудрено, ибо даже академик С.И. Вавилов, ставший впоследствии президентом АН СССР, в 1928 г. признавал: "Если бы явление Саньяка было открыто раньше, чем выяснились нулевые результаты опытов (с интерферометром Майкельсона) второго порядка, оно, конечно, рассматривалось бы как блестящее экспериментальное доказательство эфира" [29]. Но далее С.И. Вавилов пишет, что данные ротационные эффекты не противоречат теории относительности, поскольку эта теория не рассматривает вращательное движение...
Может поэтому и в знаменитой "Теории поля" Л.Д. Ландау и Е.М. Лифшица [14]
движению света по замкнутому контуру длиной L, охватывающему площадь S на
диске вращающемся с угловой скоростью ?, отведена всего одна страница. Тем не менее авторы делают вывод, что скорость света, измеренная как отношение длины контура L ко времени t, которое проходит между отправлением и возвращением луча света, составляет величину
(4.2)
Взломать лед замалчивания эффекта Саньяка, противоречившего теории относительности, заставило лишь в 70-е годы дальнейшее развитие техники. Лазерные гироскопы, работа которых основана на эффекте Саньяка, теперь широко используются в ракетной технике и авиации, так как они оказались и легче, и точнее механических гироскопов [30].
В связи с изложенным в данном разделе не лишним будет напомнить, что попытки объяснить наличие у элементарных частиц спина - h как результата механического вращения частицы вокруг своей оси наталкивались на необходимость признать, что тангенциальная скорость движения "поверхности" частицы при таком вращении должна намного превышать скорость света С. Это останавливало развитие мысли в данном направлении и привело к пониманию спина лишь как квантового числа, не связанного с механическим вращением частицы. Теперь, после анализа положения вещей, осуществленного в [9], мы видим, что ограничений на скорость вращения не существует, а потому не исключено, что элементарные частицы действительно вращаются со сверхсветовыми скоростями.
СТО не отрицала движения во времени, а только не акцентировала внимание на нем, остерегаясь широкого обсуждения парадоксов четырехскорости, о которых мы говорили в разделе 1.2. Но и в теории движения во времени, развитой в [8], появляются парадоксы, не менее интересные, чем в СТО. В книге [9] описан, например, такой.
Если ускоренная элементарная частица - тардион в своем движении во времени отстает от окружающих ее неподвижных предметов лаборатории, то эта частица должна бы, по идее, вдруг бесследно исчезнуть из нашего поля зрения как бы в никуда, оставшись в нашем вчерашнем дне, в то время как мы вместе с лабораторией уже перешли в следующий момент времени. На практике же ускоренные частицы -тардионы не исчезают, а вместе с нами благополучно кочуют в будущее. Просто в них медленнее, чем у нас, протекают все внутренние процессы. Значит, движение во времени - это лишь внутренний процесс каждой частицы - тардиона? А вычерчивавшаяся нами и нашими предшественниками ось времени - это всего лишь математическая формальность, абстракция, не более того?
Но тогда четырёхмерное пространство-время, с которым имеет дело теория относительности, - это всего лишь математический образ?! Неужели на самом деле существует только обычное трехмерное пространство?
Еще Птолемей писал на тему о размерности пространства и утверждал, что в природе не может существовать более трех пространственных измерений. И. Кант в XVIII веке, подчеркивая, что причина трехмерности нашего пространства ещё неизвестна, отмечал, что только в трехмерном пространстве гравитационные силы могут быть обратно пропорциональны квадрату расстояний между телами. В XX веке П. Эренфест и Дж. Уитроу показали, что если бы число измерений пространства было больше трех, то существование планетарных систем было бы невозможным. Материальная точка в четырехмерном пространстве либо падала бы на силовой центр, либо уходила бы от него в бесконечность. Только в трехмерном мире могут существовать устойчивые орбиты планет в планетных системах [31 ].
Почему же тогда развитый в [8] формализм движения тел во времени как вдоль четвертой оси координат с учетом динамических характеристик этого мнимого движения так красиво и просто приводит к хорошо согласующимся с экспериментальными данными результатам, если четвертой оси координат не существует?
Ответ подсказывает теория электрона, разработанная В. М. Мигуновым из Запорожья [18]. Представьте себе движение электрического сигнала по цилиндрической спирали электроплитки. Он бежит по проволоке спирали со скоростью света. Это движение по цилиндрической спирали складывается из двух взаимно перпендикулярных компонент: движения вдоль оси спирали и движения по окружности витков проволоки. Скорости указанных компонент суммируются как векторы по теореме Пифагора, т.е. по формуле, аналогичной (1.16). Чем растянутее спираль, то есть чем больше ее шаг, тем больше скорость движения сигнала вдоль ее оси и тем меньше скорость и частота кругового движения. Если же спираль туго сжата с торцов в один виток-кольцо, то остается только круговое движение сигнала. Этот случай соответствует покоящейся в пространстве частице. Она неподвижна в пространстве, но сигнал (материя) в ней мчится по кругу со скоростью света.
Мигунов утверждает, что это и есть модель элементарной частицы. Только диаметр кольца в ней меньше классического радиуса электрона. А далее вспомним, что момент количества движения mCR материи в частице должен квантоваться, и запишем:
(4.3)
, где v0- частота вращения частицы, h - постоянная Планка.
Поэтому из (4.3) получается
(4.4)
Мигунов в [18] указывает, что соотношения (4.3) и (4.4) впервые получил еще в 20-е годы Луи де Бройль, который, как и мы сейчас, пытался найти связь между полной энергией частицы и частотой внутренних процессов в ней.
Если частица имеет конечный радиус R, то тангенциальная скорость движения материи в частице составляет величину
(4.5)
где
. Отождествляя внутренне вращательное движение частицы с ее движением во времени, приравняем скорость последнего уС с тангенциальной скоростью Vт. Тогда понятно, что с уменьшением ут при неизменном R частота v должна уменьшаться:
(4.6)
(4.7)
Для этого он, исходя из выражения для полной (релятивистской) энергии частицы Е = Е0/y и учитывая (4.4), записал:
(4.8)
(4.9)
Так родилась теория де Бройля с ее непонятными "волнами материи" (позже названными "волнами де Бройля"). Их групповая скорость Vгр = dЕ/dР соответствовала скорости V движения в пространстве частицы, имеющей импульс P = mV,a вот фазовая скорость Vф = E/P = С2(с в квадрате)/V принимала значения, большие скорости света С. Теоретики до сих пор заявляют, что фазовая скорость волны де Бройля относится к числу "принципиально ненаблюдаемых величин и имеет чисто символическое значение", (см. стр. 487 в [17]). Но думается, что теоретики опять поспешили с выводами, и на самом деле фазовая скорость волн де Бройля как-то связана с виртуальными частицами - тахионами, играющими немаловажную роль в процессах движения досветовых частиц - тардионов.
В теории де Бройля частота v1 уже не имела отношения ни к какому внутреннему процессу и возрастала с увеличением скорости V поступательного движения частицы, как возрастает частота фотона с ростом его энергии.
А отложенная де Бройлем в сторону первоначальная идея пролежала полвека, пока с нее не "стряхнул нафталин" украинский физик В.М. Мигунов.
Но обратите внимание на то, что полученная Луи де Бройлем формула (4.7) совпадает с формулой (3.6) для энергии движения тела во времени Ет. Не говорит ли это о том, что энергия движения элементарной частицы во времени Eт - это энергия внутреннего движения материи в частице?
Данная мысль смыкается с высказанным выше предположением о том, что мнимое движение во времени - это лишь внутренний процесс каждой элементарной частицы, к которому мы пришли из совершенно других предпосылок. Отождествление кругового движения материи в элементарных частицах с движением их во времени наводит на мысль и о том, что движение во времени элементарных частиц - тардионов не имеет внешней направленности. Траектория движения тардиона во времени должна быть не прямолинейной, а замкнутой внутри элементарной частицы. И когда мы чертим прямую ось времени, то как бы разматываем, распрямляем и натягиваем по прямой "нить времени", которая на самом деле как бы намотана на шпулю внутри элементарной частицы и вытягивается в цилиндрическую спираль при ее движении в пространстве. Не потому ли движение во времени мнимо, что это внутренне круговое движение в частице?
Последнее великолепно согласуется с теорией Калуцы - Клейна, предложенной еще в 20-е годы. В ней предполагается, что пространство-время имеет столько дополнительных измерений, сколько разного рода полей существует в природе. Но каждая дополнительная ось координат, начиная с пятой, как предположил 0. Клейн, "свернута" в петлю с диаметром ~10-32(10 в минус 32 степени) см (планковская единица длины). Поэтому движение вдоль такой оси координат ненаблюдаемо в макромире, но проявляется в виде разного рода полей. Электромагнитному полю, по Т. Калуце, соответствует пятое измерение.
В свете вышеизложенного нам остается только предположить, что ось времени тоже свернута в петлю с размерами порядка планковских. И что движение вдоль этой четвертой оси координат - оси времени - проявляется в виде гравитационного поля и сил инерции, что не противоречит теории Эйнштейна. Чем медленнее движение во времени, тем больше релятивистская масса и инерция тела, тем больше напряженность создаваемого им гравитационного поля.
Отождествление кругового движения материи в элементарной частице с движением ее во времени возвращает нас к старому спору о том, прямолинеен или цикличен ход времени. В античные времена наблюдения за распространенными тогда солнечными часами, стоявшими на центральной площади каждого города, привели философов к выводу, что "Время не подобно прямой линии, а описывает окружность" (Прокл, V в. н. э.). Эта точка зрения отражала единство противоположностей: ограниченность и вместе с тем бесконечность, обеспечиваемые свойствами окружности.
Объединение двух других противоположностей - замкнутости движения по окружности и безграничности прямолинейного движения - достигается в спирали, что подметил еще Архимед. Это объединение и используется в описанной выше спиралеобразной модели движения.
А.Д. Чернин в своей книге [32] указывает, что спиралеобразные узоры, символизирующие время, археологи находили на сосудах IY-III тысячелетий до н. э., а также на календаре, вырезанном на бивне мамонта, найденном в Сибири. Значит, мы не первые. И это радует, ибо древние люди знали кое-что такое, до чего мы еще не додумались. Наверно, они несли с собой отголоски каких-то очень глубоких знаний предыдущих цивилизаций.
Получив в начале 20-х годов так удивившую его формулу (4.7) для внутренней энергии вращающейся элементарной частицы, Луи де Бройль почему-то не обратил внимания на то, что она очень напоминает уже известную к тому времени формулу Планка-Лауэ (3.13) для релятивистского преобразования количества теплоты, и отказался от своей формулы. Теперь понятно, что совершенно напрасно отказался. Он, видимо, тоже со временем понял это. Потому-то в 60-е годы Луи де Бройль с таким энтузиазмом отстаивал формулы Планка и Лауэ [20].
Но некоторые толкователи теории относительности, например [33], и в наши дни вопреки (4.7) утверждают, что чем быстрее вращается тело, тем больше должна быть его полная масса-энергия, потому-де, что к энергии покоя этого тела добавляется кинетическая энергия вращения тела. Попробуем сосчитать так ли это.
Рассмотрим планету с массой m0, обращающуюся с тангенциальной скоростью Vт по круговой орбите с радиусом R вокруг Солнца или другой звезды, имеющей массу М. Центробежной силе
(4.10)
(4.11)
учитывающая возрастание массы планеты при движении ее со скоростью Vr.
Орбита планеты равновесна, если указанные силы уравновешивают друг друга:
(4.12)
Подставим в (4.12) значения Fц и Frp из (4.10) и (4.11 ) и найдем из получившегося развернутого уравнения выражение для радиуса равновесной (устойчивой) орбиты.
(4.13)
(4.14)
На устойчивой круговой орбите планета обладает кинетической энергией движения по орбите:
(4.15)
- энергия покоя планеты, Еп = Ео/ут - ее полная (релятивистская) энергия.
С другой стороны, планета в гравитационном поле удерживающей ее звезды обладает потенциальной гравитационной энергией
(4.16)
Ниже мы увидим, что эта энергия отрицательна отнюдь не условно, а потому, что она уходит из связанной силами тяготения системы.
Из формулы (4.13) понятно, что фигурирующая в (4.16) комбинация GM/R определяет квадрат тангенциальной скорости Vr движения планеты по равновесной круговой орбите. И тогда, подставив в (4.16) ещё и значение m = m0/yr, получим вместо (4.16) ещё одно выражение для потенциальной энергии планеты в гравитационном поле звезды:
(4.17)
(4.18)
(4.19)
раз больше первой. Подчеркнем: при первой соблюдается равенство противодействующих сил, при второй - энергий, связанных с ними.
А теперь вычислим суммарную энергию планеты. Она состоит из суммы энергий покоя Е0, кинетической Ек и потенциальной Епот и составляет