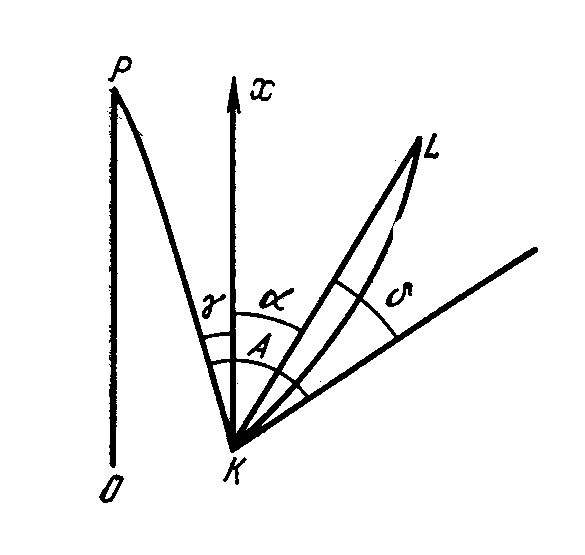- -- Общие сведения о проекции Гаусса -- Крюгера
L0 = 6®n -- 3®,
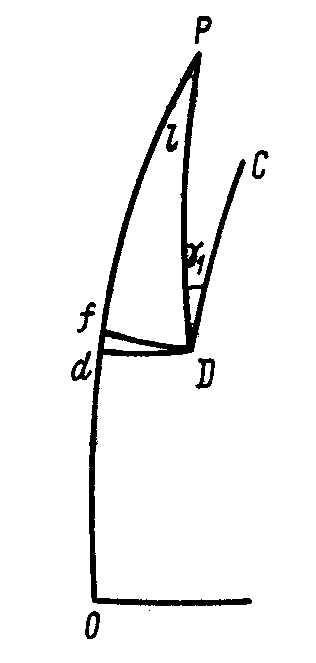
Рис. 2.1
(2.1)
, (2.2)
(2.3)
sin и sin l по два члена ряда, получаем
можно принять
, тогда
. (2.4)
(2.5)
.
) определим tg В:
tg В = cos l tg Bf.
возьмем два члена ряда, тогда
можно принять
в формулу для sin(Bf -B),
, в ввиду его малости, отброшен). Делая дальнейшие преобразования, последовательно получаем
6 cos2 В -- 1 = 6 cos2 В -- sin2 В -- cos2 В = 5 cos2 В -- sin2 В,
(2.6)
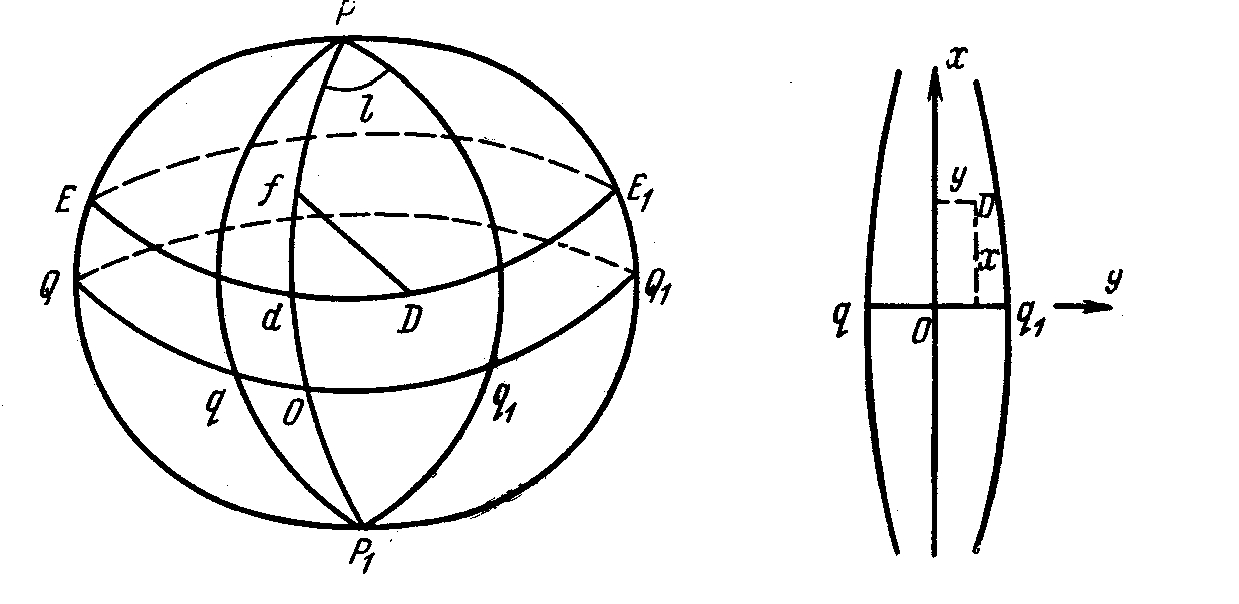
.
m =
.
m = n =
.
cos -- в ряд и возьмем три члена ряда, тогда
(3.1)
следует, что ордината уc зависит от широты и долготы точки, поэтому масштаб в каждой точке проекции различный и искажения зависят от удаления точки от осевого меридиана зоны по оси у (табл. 3.1).
Таблица 3.1
Масштабы на краю шестиградусной зоны (при l = 3®)
|
Масштаб |
Широта |
||||||
|
|
0® |
15® |
30® |
45® |
60® |
75® |
90® |
|
|
1,0014 |
1,0013 |
1,0010 |
1,0007 |
1,0004 |
1,0001 |
1 |
|
|
1,0028 |
1,0026 |
1,0020 |
1,0014 |
1,0008 |
1,0002 |
1 |
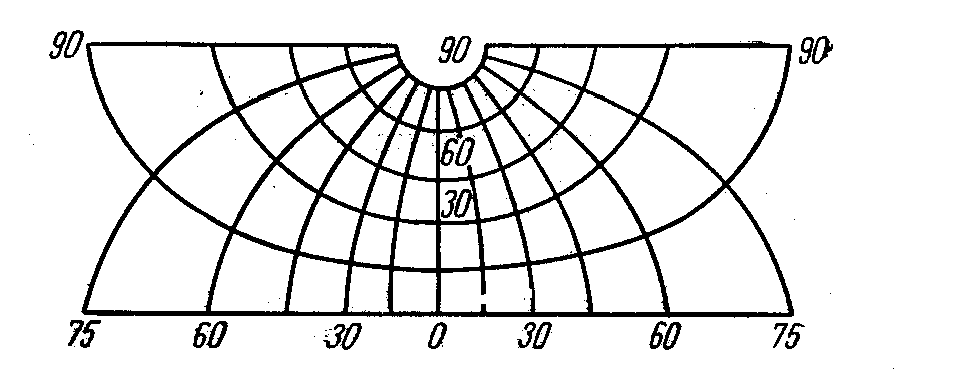
Рис. 3.3
(4.1)
будем иметь
взято для ус приближенное его значение
.
. (4.2)
(4.3), (4.4)
.
.
.
(4.5)
b"=- (Bf -- В)"; s = х -- Х..
(4.6)
(4.7)
B = Bf - (Вf -- В). (4.8)
(4.9)
L = L0 + l, (4.10)
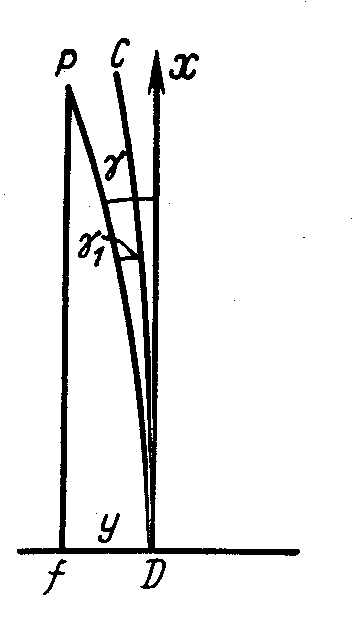
Рис. 5.1
) Гауссово сближение меридианов ? очень мало отличается от геодезического сближения меридианов ?1 и практически их можно считать равными. Точная формула для Гауссова сближения меридианов такая
(5.1)
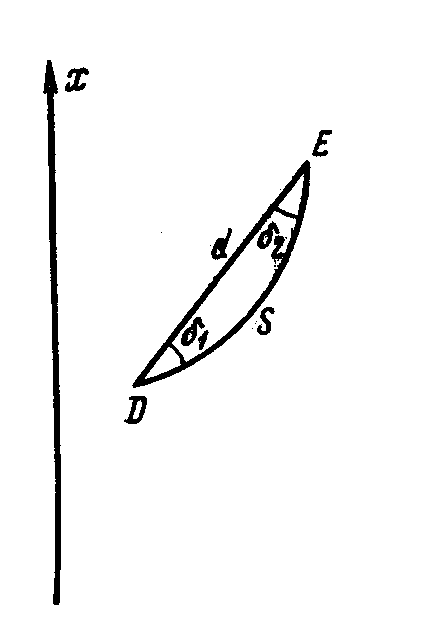
Рис. 6.1
) для масштаба изображения два первых члена ряда и напишем
ds=s и dS=S.
(6.1)
всегда положительная, следовательно, длины изображений линий в проекции Гаусса -- Крюгера всегда больше длин соответствующих линий на поверхности эллипсоида. Это также видно и по величине масштаба, так как он больше единицы. Формула (6.1) показывает, что при переносе линий с поверхности эллипсоида на проекцию нужно во все измеренные линии вводить поправку, равную
. Эта поправка называется р е д у к ц и е й р а с с т о я н и я.
(6.2)
Табл. 6.1
Относительные искажения длин линий на краях 6® зоны в различных широтах
|
Широта |
Относительные искажения |
|
0® |
1 : 720 |
|
30® |
1 : 1000 |
|
45® |
1 : 1430 |
|
60® |
1 : 2500 |
1g (1+ х) = ?х,
Табл. 6.2
Относительные искажения в зависимости от удаления (от величины ym ) линии
От осевого меридиана зоны
|
В километрах |
Относительные искажения |
В километрах |
Относительные искажения |
|
50 |
1 : 32 000 |
200 |
1 : 2500 |
|
100 |
1 : 8000 |
250 |
1 : 1300 |
|
150 |
1 : 3500 |
300 |
1 : 900 |
(6.3)
(6.4)
(6.5)
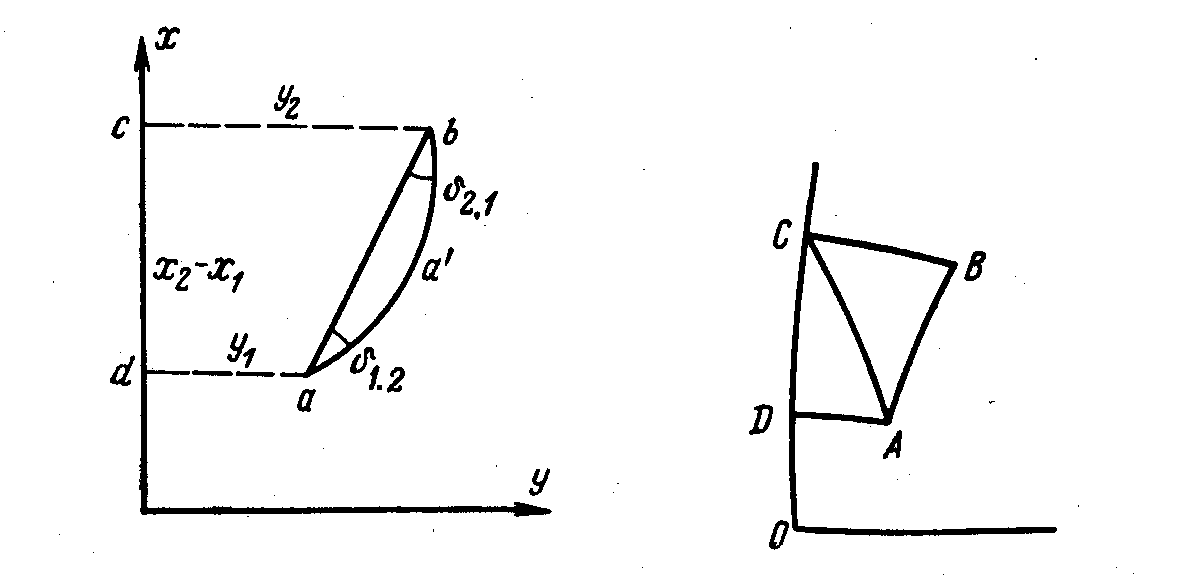
? = 360® + ?1 + ?2
?1 = 360® + ?1.2 + ?2.1,
?1.2 + ?2.1 = ?1 + ?2.
или
?1 + ?2 = ?1.2 + ?2.1 =
.
?1.2 = ?2.1 =
.
?''1.2 = ?''2.1 =f(x2 - x1 )ym (7.1)
?''2.1 = - ?''1.2 , (7.2)
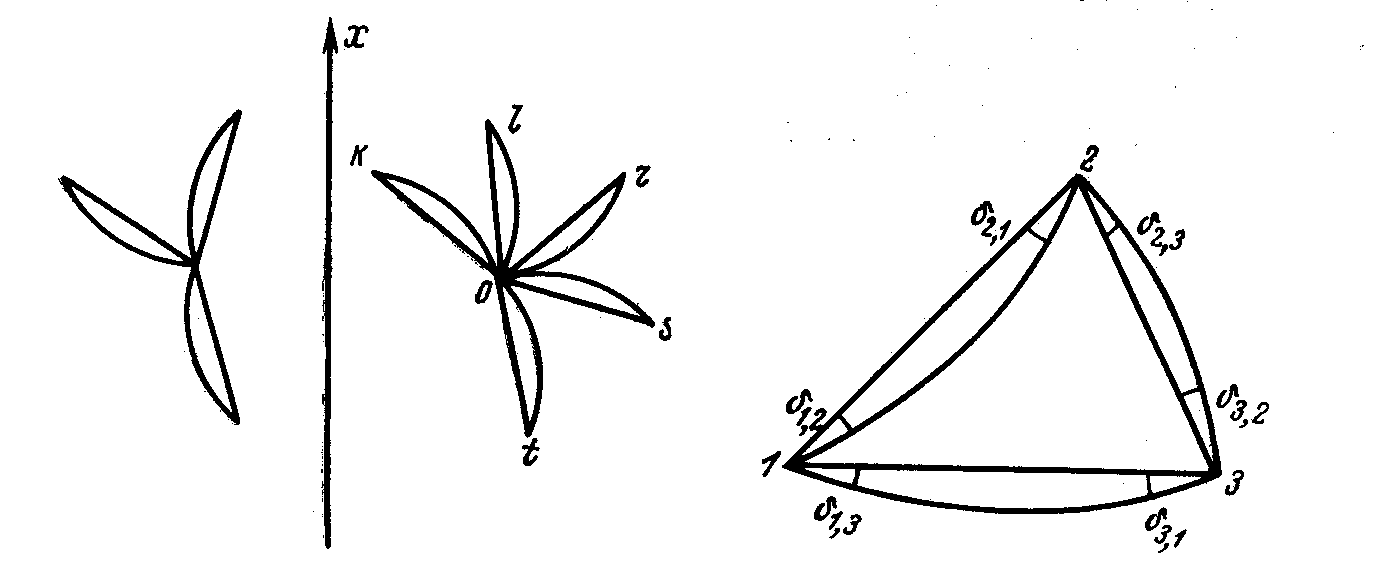
(7.3)
kol (рис. 7.3), редуцированный на плоскость, равен
.
180® = 180® + ? + (?1.2 - ?1.3) + (?2.3 - ?2.1) + (?3.1 - ?3.2)
(?1.2 - ?1.3) + (?2.3 - ?2.1) + (?3.1 - ?3.2) = - ? (7.4)
. (7.5)
(7.6)
. (7.7)