МИНИСТЕРСТВО ОБРАЗОВАНИЯ
И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Новосибирский национальный исследовательский государственный университет" (Новосибирский государственный университет, НГУ)
Философский факультет
Кафедра: Логики и методологии науки
Кормин Михаил Викторович
МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ
Формализация и принятие решений
Новосибирск, 2012
|
|
|
|
|
|
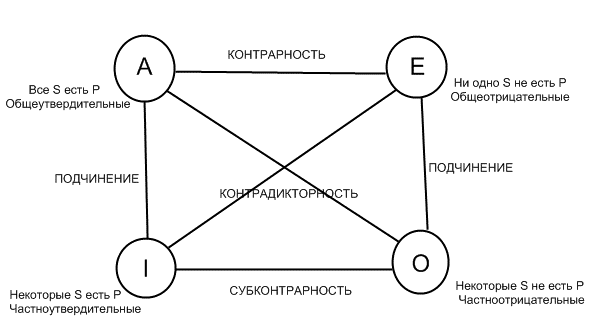
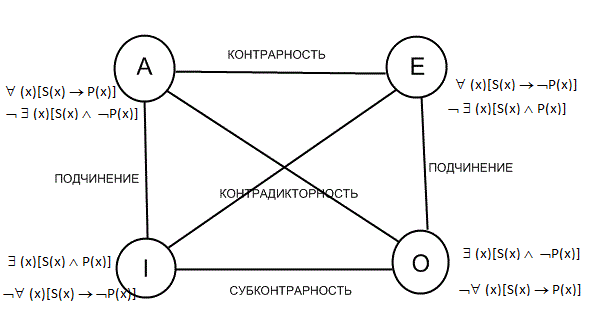
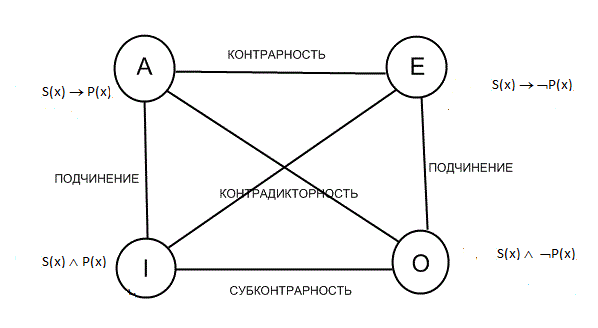
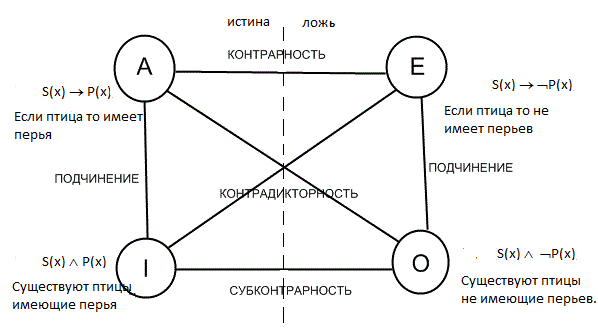
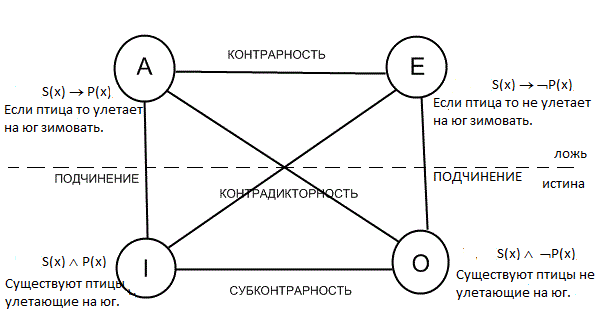
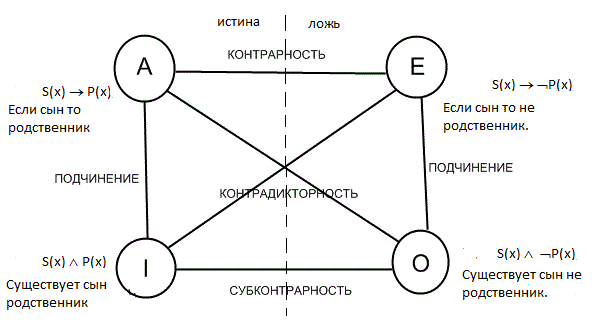
Родовая связь
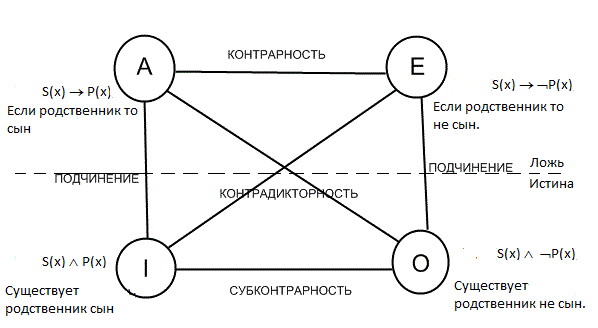
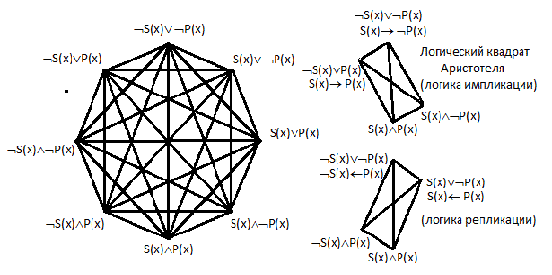
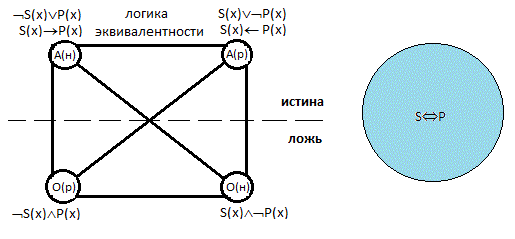
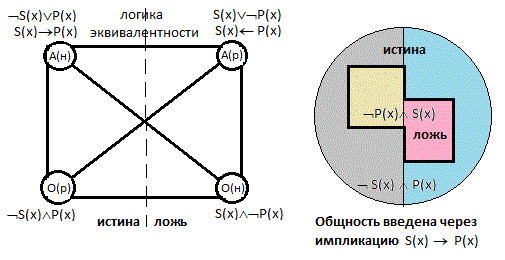
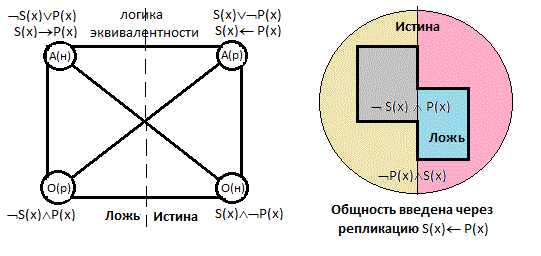
либо не заключили её Ǝ(х)Ǝ(у) -S(x,у)
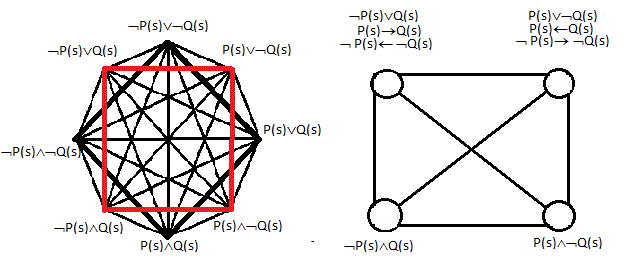
Ǝ(х)Ǝ(у)ƎS(x,у)[Р(s)-˂-˃Q(s)] А это уже два потенциальных варианта логических взаимоотношений находящихся под квантором общности. Для наглядности представим эти отношения в графической форме.