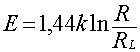Кириллов Михаил Александрович : другие произведения.

Психофизические законы и экономика

Самиздат: [Регистрация] [Найти] [Рейтинги] [Обсуждения] [Новинки] [Обзоры] [Помощь|Техвопросы]
Ссылки:
Школа кожевенного мастерства: сумки, ремни своими руками
 Ваша оценка:

Психофизические законы и экономика

  
   Экономическая подсистема является фундаментальной и неотъемлемой частью более широкой социально-экономической системы. Основным элементом, в интересах которого создаются, функционируют и совершенствуются такие системы, следует признать человека, индивидуума. Поэтому, в первую очередь, нас должны интересовать присущие каждому отдельному человеку, характеристики и параметры, а также возможности их количественного измерения в общепринятых физических величинах.
   К числу таких параметров, относятся потребности и способности человека, его интересы, испытываемые им ощущения и удовольствия. Несмотря на огромное количество действующих на человека стимулов, в качестве которых можно рассматривать и потребляемые им товары (услуги), конечный смысл такого потребления сводится к получению необходимых для обеспечения его нормальной жизнедеятельности количеств энергии и информации. Используемые для этого способности человека также могут быть выражены в единицах измерения энергии и информации. Человек, как физическая система, регулярно обменивается с окружающим его миром энергией и информацией.
   Для выявления физического смысла перечисленных выше терминов и обоснования возможности измерения интересующих нас параметров в общепринятых единицах необходимо обратиться к результатам тех исследований, которые еще в позапрошлом веке выполнил основатель психофизики Г.Т.Фехнер [1,2,3,4].
   Используя экспериментально установленное Э.Г.Вебером [5,6] соотношение:
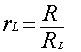   0x01 graphic , (1)
   где R - величина действующего на человека раздражителя (стимула);
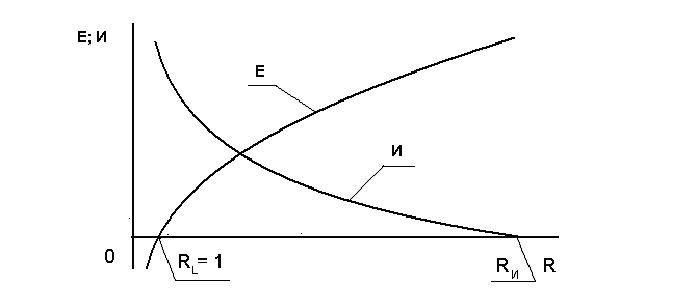
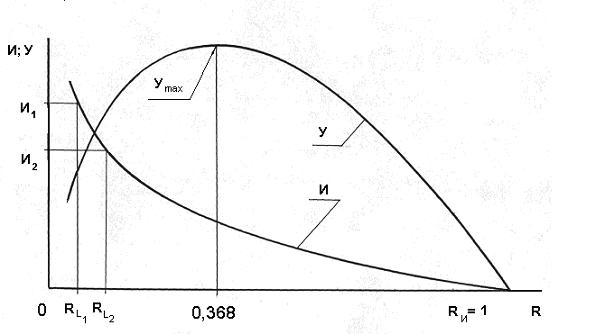
   0x01 graphic - прирост раздражителя, впервые замечаемый человеком,
   Г.Т.Фехнер теоретическим путем вывел свой закон, выражающий зависимость ощущений человека от величины воздействующего стимула (раздражителя):
   0x01 graphic , (2)
   где Е - величина испытываемого человеком ощущения;
   R - величина действующего стимула;
   RL - пороговое значение стимула, при котором ощущение
   еще не возникает;
   k - коэффициент пропорциональности.
   Физический смысл коэффициента пропорциональности (k) сводится к учету различий в испытываемых отдельными индивидуумами ощущениях.
   Далее Г.Т.Фехнер ввел понятие фундаментальной величины стимула (rL):
   0x01 graphic , (3)
   И в окончательном виде закон Г.Т.Фехнера (при принятом им условии RL = 1) приобретает вид (рис.1):
   Е=1,44k ln rL , (4)
   Графически этот закон, а также закон, устанавливающий зависимость интереса от величины действующего стимула, о котором речь пойдет ниже, представлены на рис.1.
   0x01 graphic
Рис.1. Зависимости ощущения и интереса от величины стимула.
   Параметр rL в выражении (4) является безразмерным и может быть определен из выражения (3), в котором величины R и RL измеряются в тех или иных единицах, исходя из физического смысла действующего стимула. Вопрос количественной оценки величины самого ощущения Е остается открытым. Сам Г.Т.Фехнер, полагая, что ощущение невозможно измерить непосредственно, поскольку оно субъективно, предложил косвенный метод получения искомой величины, которая может быть определена как сумма едва заметных различий (ЕЗР) в ощущениях. При соблюдении исходного соотношения (1) сумма равных между собой ЕЗР откладывается по оси ординат. Однако использование этого показателя не решает проблемы измерения ощущений, и обоснование такой единицы остается крайне необходимым. Логарифмический закон Г.Т.Фехтнера должен надежно работать при том условии, что все величины действующего на человека стимула имеют равную вероятность.
   Наличие экспериментального материала, не укладывающегося в закон Г.Т.Фехтнера, заставило С.Стивенса [7] предложить степенной закон изменения величины ощущения от действия стимула. Попытку объединения двух законов предпринял отечественный исследователь Ю.М.Забродин [8].
   Не вдаваясь во все тонкости логического обоснования основного психофизического закона, вернемся к вопросу измерения величины ощущения в законе Г.Т.Фехнера, который столь же актуален и для других трактовок закона.
   Можно предположить, что, при равной вероятности воздействия всех возможных значений стимула, величину ощущения, выраженную в битах на единицу стимула, позволяет получить предложенная Р.Хартли [9] формула для определения количества информации:
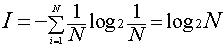   0x01 graphic , (5)
   где N - число равновероятных событий.
   Закон Г.Т.Фехнера фактически идентичен выражению (5) за исключением коэффициента к, который отражает способность конкретного индивидуума к восприятию информации и в частном случае может быть равен 1.
   Сам Р.Хартли прекрасно понимал, что разные сообщения (стимулы) имеют различную вероятность, и, следовательно, неожиданность их появления для получателя неодинакова. Однако он решил, что фактор "неожиданности" "относится к компетенции психологии и не должен интересовать инженера-связиста" [9].
   Хотя предлагаемый принципиальный подход и последующие рассуждения не зависят от конкретного вида кривой (логарифмической, степенной или какой-либо другой, вытекающей из обобщенного закона Ю.М.Забродина), в дальнейшем мы будем пользоваться именно логарифмической зависимостью, позволяющей объяснить физический смысл измерения и существенно упростить математические выкладки.
   В соответствии с негэнтропийным принципом, предложенным Л.Бриллюэном [10], приобретение некоторого количества информации неизбежно уменьшает энтропию системы на ту же самую величину.
   Необходимость поиска аналогичного процесса отметил Ф.Ф.Драгель [11]: "...философские основания психологии диктуют необходимость каждому ощущению иметь свою противоположность, - и далее, - ... между тем, развивающаяся эмпирическая медицина до сих пор не замечала этого".
   Если ощущения человека отражают получаемую им информацию, то соответствующее уменьшение энтропии можно рассматривать как противоположность, связав её с изменением интереса человека к тому или иному стимулу (раздражителю, воздействию, и др.) в зависимости от их интенсивности или количества.
   Изменение интереса человека по аналогии с его ощущением также опишем логарифмической функцией. Её вид может быть определен методом, использовавшимся Г.Т.Фехнером при выводе своего закона, с той лишь разницей, что вместо пороговой величины стимула RL используется другая пороговая величина RИ, при которой интерес индивидуума к воздействующему стимулу становится равным 0.
   Полученная таким образом новая функция, описывающая адекватное испытываемому ощущению изменение интереса от величины действующего стимула, имеет вид:
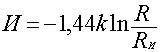   0x01 graphic , (6)
   где И - величина проявляемого человеком интереса к
   действующему стимулу;
   R - действующая величина стимула;
   RИ - пороговое значение стимула, при котором интерес
   падает до 0;
   k - коэффициент пропорциональности ( тот же , что и в
   законе Г.Т. Фехнера).
   Графически функция интереса (6) представлена на рис.1.
   Сумма величин испытываемого ощущения и соответствующего ему интереса есть величина постоянная для любого стимула:
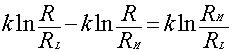   0x01 graphic , (7)
   Несмотря на то, что пороговые величины стимула RL у разных индивидуумов не равны между собой, Г.Т.Фехнер принял эту величину равной 1. Пороговую величину RИ также можно принять за 1. При этом выражение (6) примет вид:
   И = - 1,44 k ln rИ ,(8)
   где rИ- вторая фундаментальная величина стимула (в отличие от
   первой, введенной Г.Т.Фехнером):
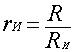   0x01 graphic , (9)
   График выражения (8) представлен на рис.2.
   При RИ = 1 пороговые величины RL1 и RL2 для двух разных индивидуумов окажутся неодинаковыми, наглядно отражая их различную чувствительность к действию стимула, и различную величину их интереса И1 и И2, что показано на рис.2. Величина интереса измеряется в битах на единицу стимула.
   0x01 graphic
Используя зависимость (8) интереса от величины действующего стимула и саму величину стимула, можно получить новую чрезвычайно интересную функцию удовольствия человека, которой З.Фрейд [12] придавал императивное значение.
   Y = - 1,44k rИ ln rИ , (10)
   Графически она представлена на рис.2.
   0x01 graphic
   Рис.2 Зависимости интереса и удовольствия от величины стимула
  
   Как хорошо видно из графика, эта функция в отличие от зависимостей (4), (6) и (8) имеет экстремум, который можно вычислить, продифференцировав выражение (10). Соответствующая величина rИЭ, при которой Y достигает максимума, оказалась постоянной и в принятых для её измерения относительных единицах одинаковой для всех индивидуумов:
   rИЭ = e-1 = 0,368 = const , (11)
   Функция (10) отражает количество удовольствия, получаемого человеком в зависимости от величины действующего на него стимула, которое адекватно количеству вновь приобретенной информации или уменьшению энтропии. Единица измерения - бит.
   Далее необходимо поставить вопрос об области определения функций: ощущения, интереса, удовольствия, поскольку величина воздействующего стимула R теоретически может быть как меньше RL , так и больше RИ .
   Это весьма сложная задача, предполагающая необходимость количественной оценки величин информации и энтропии в нейронных системах головного мозга человека, на которые воздействуют изменяющиеся в широких пределах стимулы. Если изменение количества информации и энтропии в этих системах может осуществляться в более широких пределах, чем это происходит в результате воздействия стимула (как, например, отрицательные ощущения в законе Г.Т.Фехнера), то все три функции будут иметь смысл и за пределами диапазона, ограниченного пороговыми значениями стимулов RИ и RL. В данной работе возможность изменения функций ощущения, интереса и удовольствия за этими пределами не рассматривается и область их определения считается заданной в пределах 0x01 graphic .
   Отдельный индивидуум, а тем более некоторое их множество (общество), характеризуются присущими им разнообразными интересами, способностью испытывать широкую гамму ощущений и удовольствий. В связи с этим возникает задача определения обобщенных (суммарных) характеристик как отдельного индивидуума, так и того или иного их множества.
   Суммирование выражений (2), (8) и (10), отличающихся величиной коэффициента к, характерной для каждого отдельного индивидуума, позволяет получить обобщенные характеристики некоторого множества ощущений, интересов и удовольствий в виде следующих функций:
   Е1 +Е2+... +Еn = 1,44 (к1+к2+... +кn) ln rL , (12)
   И1+И2+...+Иn = - 1,44(к1+к2+... +кn) ln rИ , (13)
   Y1 +Y2+... +Yn = - 1,44(к1+к2+... +кn) r И ln rИ , (14)
   В точке экстремума, в которой логарифм величины rL = e равен 1, a rИ = е-1 равен -1, величину функций (12), (13) и (14) можно определить из выражений:
   Етах = 1,44(к1+к2+...+кп), (15)
   Иmax = - 1.44 (к1+к2+... +кn) , (16)
   Ymax = - 1.44 (к1+к2+... +кn) rИ , (17)
   Полученные в настоящей работе новые функции интереса и удовольствия, отражающие реакции человека на действие различных стимулов, которые в экономической системе выступают в виде товаров, предлагается в качестве гипотезы считать аналогами экономических понятий цены и дохода. Данные функции наряду с другими положениями, изложенными в следующих работах, составляют основу предлагаемой концепции экономики, которую мы обсудим ниже. Но прежде, чем перейти к изложению других важных положений этой концепции, а также метода построения различных макроэкономических моделей, необходимо остановиться на проблеме денег, которые играют весьма существенную роль в экономике. Этому вопросу и будет посвящена вторая статья.

Основные выводы

   1. К числу основных характеристик психической деятельности человека относятся его ощущения, интересы и удовольствия.
   2. Предложены два новых закона, отражающих изменение интереса и удовольствия от величины действующего стимула, а также установлена функциональная связь между ощущением, интересом и удовольствием человека.
   3. Величину ощущения, интереса (цены) и удовольствия (дохода) предложено рассчитывать с помощью полученных в работе зависимостей. Размерность величины ощущений и интересов - бит на ед./стимула, удовольствий - бит.
   4. Приведенные в работе характеристики психической деятельности человека могут быть положены в основу ряда научных дисциплин, которые занимаются изучением различных аспектов деятельности и поведения индивидуума или сообщества, в частности, экономики и социологии.

Литература

   1. Fechner G. Elemente der Psychophysik. 1 Aufl. Leipzig. 1860; 2 Aufl. Leipzig. 1889.
   2. Fechner G. In Sachen der Psychophysik. Leipzig. 1877.
   3. Фехнер Г.Т. О формуле измерения ощущений. // Проблемы и
   методы психофизики / под ред. А.Г. Асмолова и М.Б.
   Михалевской. - М.: Изд-во МГУ. 1974. С.13-19.
   4. К.В. Бардин Основной психофизический закон и его варианты //
   Проблемы психофизики и дифференциальной психофизиологии /
   под ред. Кашина А.П. Изд-во Казанского ун-та. 1981.
   5. Weber E. De tacto // "Annotationes anatomical et
   physiologicae". Leipzig . 1834.
   6. Weber E. // The sense of touch. N.-Y. 1978.
   7. Стивенс С. С. О психофизическом законе // Проблемы и
   методы психофизики / под ред. А.Г. Асмолова и М.Б.
   Михалевской. - М.: Изд-во МГУ. 1974. С. 56-102 .
   8. Забродин Ю.М. Введение в общую теорию сенсорной
   чувствительности // Психофизические исследования / под ред.
   Б.Ф. Ломова и Ю.М.Забродина. - М.: "Наука".1977.С.31-125.
   9. Хартли Р. Математическая теория связи // Теория
   информации и ее приложения. - М. 1959.
   10. Бриллюэн Л. Наука и теория информации. - М. 1960.
   11. Драгель Ф.Ф. Общая теория процесса ощущения
   антиощущения организмом воздействий среды - основа
   методологии познания сущности паба1 и других
   психофизических процессов в ортопедии // Профилактика,
   комплексное лечение и медико - социальная реабилитация
   детей с заболеваниями опорно- двигательного аппарата:
   тезисы докл. / под ред. В.Л. Андрианова. - Владимир. 1988.
   12. З. Фрейд По ту сторону принципа удовольствия //
   Психология бессознательного. - М.: "Просвещение". 1989.
   С. 382 - 424.
  
  
  
  
   Примечание:
   Вместо используемого в данной работе термина "интерес" Г.Т.Фехнер применял термин "стремление", а З.Фрейд [12] - "влечение".
  
  
  
  
  
 Ваша оценка:
Связаться с программистом сайта.

Новые книги авторов СИ, вышедшие из печати:
О.Болдырева "Крадуш. Чужие души" М.Николаев "Вторжение на Землю"

Как попасть в этoт список

Кожевенное мастерство | Сайт "Художники" | Доска об'явлений "Книги"