__________________________________________________________________

ВСТУП

Незважаючи на колосальну кiлькiсть сучасних матерiалiв, що мають велике розмаїття властивостей, iнодi вражаючих, одним з основних типiв конструкцiйних матерiалiв залишаються сталi. Це недивно, тому як саме матерiали на основi залiза мають унiкальне поєднання вiдносно низької вартостi i високих механiчних i експлуатацiйних властивостей, якi, в свою чергу, можуть вiдповiдно умов iнженерної задачi змiненi в широких межах за рахунок легування й обробки. Систем легування розроблено безлiч, так саме як i створена велика кiлькiсть технологiй деформацiйної, термiчної, деформацiйно-термiчної, хiмiко-термiчної обробки. Не дивлячись на той факт, що сталi вiдомi людству з давнiх часiв, вони не тiльки не втратили актуальностi як незамiнний матерiал, але i потенцiал дослiдження металофiзики й технологiй обробки матерiалiв на основi залiза далеко не вичерпано. Сучаснi сталi є складними багатокомпонентними системами, а теоретичне вивчення i моделювання процесiв, що вiдбуваються у них є непростою комплексною задачею.

Так в основi структуроутворення велику роль вiдiграють фазовi перетворення, в тому числi фазовi перетворення у твердому станi. Саме наявнiсть останнiх у багатьох матерiалiв на основi залiза обумовлює їх унiкальнi властивостi, наприклад здатнiсть до гартування на мартенсит або бейнiт. Структурний стан i властивостi сталi визначаються умовами, у яких протiкає таке перетворення, як розпад аустенiту. Це обумовлює важливiсть дослiдження термодинамiки i кiнетики вказаного процесу. Такi дослiдження, здебiльшого експериментальнi, проводилися вже досить давно. Навiть у 1928 роцi було видано один з перших довiдникiв росiйською мовою, у якому було зiбрано кiнетичнi дiаграми розпаду переохолодженого аустенiту, що однак мiстив данi по не досить великiй кiлькостi сталей. Пiзнiш було напрацьовано значну кiлькiсть матерiалiв. Так, популярний довiдник авторства Л. Є. Попової i А. А. Попова мiстить дiаграми для декiлькох сотен сталей рiзного складу. Але, як зазначалося вище, сучасна сталь є складною багатокомпонентною системою. Тому бiльш глибокий i детальний аналiз довiдникових даних показав, що у просторi безлiчi комбiнацiї набору i кiлькостi легуючих елементiв iснує досить багато "бiлих плям", у тому сенсi, що кiнетика розпаду аустенiту для них не вивчена, або вивчена недостатньо. Iнодi наявних довiдникових даних недостатньо навiть для того, щоб побудувати достовiрну емпiричну модель для певного класу сталей. Навiть для вiдомих марок сталi iнодi буває досить важко знайти термокiнетичну дiаграму. Окрiм того на кiнетику фазових перетворень впливають окрiм хiмiчного складу також такi фактори як структурний стан металу (зокрема розмiр зерна аустенiту), наявнiсть i ступiнь попередньої деформацiї. Варiювання хiмiчного складу в межах навiть однiєї окремої марки сталi також може мати суттєвий вплив на термокiнетичну дiаграму, i, як наслiдок, на структурний стан, що буде отриманий у певних умовах. Реальнi умови перетворення можуть включати непостiйну швидкiсть охолодження, в тому числi рiзко змiнну або циклiчну, обумовленi особливостями технологiчного процесу. Подiбний випадок робить данi довiдникової дiаграми, наведенi для дещо iдеалiзованих умов, лише орiєнтовними.

Експериментальнi дослiдження в областi термодинамiки фазових рiвноваг i кiнетики фазових перетворень є надiйним i достовiрним, але витратним i трудомiстким методом, що не завжди може бути швидко реалiзованим. Тому велика увага придiляється математичному моделюванню вказаних явищ. Ще у 70-х роках ХХ столiття почали активно розробляти емпiричнi моделi, що описують стiйкiсть переохолодженого аустенiту залежно вiд температури i хiмiчного складу. Розробка подiбних моделей продовжує розвиватися i у наш час. I це не дивно. Такi моделi можуть давати прийнятний результат i досить простi у створеннi, тому як не потребують глибокого проникнення у сутнiсть фiзичних явищ, а лише статистичної обробки масиву експериментальних даних i пiдбору апроксимуючих функцiй, якi, в свою чергу, не зобов'язанi мати певного фiзичного сенсу. Але їх важливим недолiком є обмеженiсть i "негнучкiсть". Тобто розповсюдження їх результатiв за межi дiапазону дослiдної вибiрки не є надiйним.

Бiльш сучасним напрямком, i в той же час бiльш складним, є розробка фiзично обґрунтованих математичних моделей. Такий пiдхiд вимагає розумiння фiзичних явищ, що лежать в основi процесiв, що розглядаються i застосування рiвнянь математичної фiзики для їх опису. Слiд зазначити, що такi моделi також потребують експериментального визначення багатьох своїх параметрiв. Але оскiльки вони є фiзично обґрунтованими визначенi параметри також можуть бути вiдповiдно iнтерпретованими як мiра певного явища чи фiзичної властивостi. Тому область застосування такої моделi є значно бiльш широкою.

Таким чином, дана робота присвячена головним чином розробцi фiзично обґрунтованих моделей, якi описують термодинамiчнi i кiнетичнi аспекти фазових перетворень, зокрема розпаду аустенiту, у сталях. Такi моделi, окрiм просто опису, наприклад, кiнетики, у якостi "побiчного продукту" дають таку цiнну iнформацiю, як данi про структуру, що утворюється в сталi в ходi перетворення, яке вiдбувається в певних умовах.

РОЗДIЛ 1

Сучаснi досягнення у сферi математичного моделювання фазових перетворень i структуроутворення у легованих сталях

Процеси фазових перетворень, зокрема у твердому станi, вiдiграють ключову роль у формуваннi структури i властивостей сталей i сплавiв. Вивчення їх має велике практичне значення. Експериментальнi дослiдження є зазвичай досить дорогими i трудомiсткими, тому набувають розвитку методи математичного i комп'ютерного моделювання. Їх основною цiллю є передбачити хiд процесiв фазових перетворень та їх результати. Отримана iнформацiя використовується для розробки i оптимiзацiї технологiй термiчної, хiмiко-термiчної i деформацiйно-термiчної обробок.

На даний час створено досить багато моделей, що описують термодинамiку i кiнетику розпаду переохолодженого аустенiту в вуглецевих i легованих сталях. Але до сих пiр найбiльш поширеними залишаються чисто емпiричнi моделi [1-5]. Вони простi у розробцi i у рядi випадкiв здатнi забезпечити достатню точнiсть. Але їх недолiком є жорстка прив'язанiсть для конкретної марки чи вузької групи сталей. Бiльш складними є фiзично обґрунтованi моделi [6-14], якi використовують рiвняння математичної фiзики для опису процесiв, що вiдбуваються. Вони є бiльш гнучкими i мають значнiшу здатнiсть до коректного передбачення у широкому дiапазонi випадкiв [6]. Але слiд зазначити, що навiть такi моделi завжди мають певну складову емпiричних параметрiв, що вимiрюються експериментально. Але необхiднi експерименти є модельними i лабораторними. Математична модель, використовуючи цi данi, здатна, в свою чергу, описати бiльш складну, наближену до реальностi систему.

1.1 Методи математичного моделювання фазових перетворень у легованих сталях

1.1.1 Емпiричнi моделi. Оскiльки емпiричнi моделi фазових перетворень через їх простоту досить часто використовуються [6] слiд розглянути їх окремо. Також подiбнi моделi можуть бути застосованi для розрахунку першого наближення, що буде уточнюватися за допомогою бiльш складної (але вибагливою до обчислювальних ресурсiв) та точної фiзично обґрунтованої моделi.

Бiльша частина емпiричних моделей для опису кiнетики розпаду аустенiту побудована на основi рiвняння Колмогорова-Аврамi [6], що має вигляд:

(1.1)

де f - об'ємна частка продукту перетворення; f^max - максимально можлива частка продукту перетворення; m та n - емпiричнi параметри.

Запропоновано цiлий ряд формул для обчислення значень параметрiв m i n. Так у роботi [4] для феритного перетворення наводяться наступнi формули:

(1.2)

(1.3)

де w_C^r - вмiст вуглецю у остаточному аустенiтi, мас. %; d_? - розмiр зерна аустенiту, мкм.

Для перлiтного перетворення формули мають вигляд:

(1.4)

n = 1.5

А для бейнiтного перетворення:

(1.5)

n = 1.5

(1.6)

Наведеннi вище формули дають досить точнi результати, але не враховують легування (окрiм марганцю i частково кремнiю) i тому пiдходять лише для вуглецевих сталей, причому тiльки доевтектоїдних [6]. В свою чергу данi про кiнетику розпаду аустенiту в подiбних сталях є вiдомими i доволi добре дослiдженi експериментально. Але модель подiбного роду не є взагалi непотрiбною. Можливою сферою застосування її може бути опис процесу, що вiдбувається на фонi фазового перетворення, де вона виступатиме як швидкообчислюваний орiєнтир.

В роботi [15] розроблено емпiричнi моделi кiнетики розпаду аустенiту, що враховують вплив бiльшої кiлькостi легуючих елементiв. Вказанi моделi являють собою набори рiвнянь регресiї, що не мають за собою нiякого фiзичного пiдґрунтя. Тому кожен набiр таких рiвнянь пiдходить лише для заданої марки сталi у досить вузькому дiапазонi варiювання параметрiв.

Модель, запропонована у роботi [16] також базується на рiвняннi (1.1), але пропонує бiльш простi формули для обчислення параметрiв m та n у порiвняннi з роботою [4]. Значення параметру n у нiй приймається за 3, а m розраховуэться за формулою (1.7).

(1.7)

(1.8)

де K₀, Q₀, Q₁, A - емпiричнi параметри;
- швидкiсть охолодження, ®С/с.

Недолiком даної моделi є те, що значення емпiричних параметрiв, що входять до неї, потрiбно визначати окремо для кожного складу сталi. Це в тiй чи iншiй мiрi притаманне бiльшостi емпiричних моделей.

Для розрахунку температури початку мартенситного перетворення у вiтчизнянiй лiтературi розповсюджена формула А. А. Попова [17]:

(1.9)

Дещо бiльш точна модель, що також описує кiнетику мартенситного перетворення, запропонована у роботi [1]. ЇЇ рiвняння наступнi:

(1.10)

де f_M - частка мартенситу при температурi T; M_S - температура початку мартенситного перетворення, К; T - поточна температура, К; m та n - емпiричнi параметри, що залежать вiд хiмiчного складу сталi.

(1.11)

(1.12)

(1.13)

Оскiльки мартенситне перетворення вiдбувається дуже швидко i за умов охолодження, то кiнетичнi формули подiбнi (1.10), що описують процес, як залежний вiд температури (яка змiнюється з плином часу), а не вiд часу є цiлком прийнятними для використання.

Одну з найбiльш точних [6] емпiричних моделей перетворення аустенiту розроблено у роботах [18-21]. Основне кiнетичне рiвняння даної моделi для низьколегованих сталей має вигляд:

(1.14)

де
- миттєва швидкiсть охолодження; n = 0,9 - параметр Аврамi; M, b₁ i b₂ - емпiричнi параметри.

Для середньолегованих сталей:

(1.15)

(1.16)

де m, b₀, b₁ та b₂ - емпiричнi параметри.

Вищевказана модель покладена в основу комп'ютерної програми HSMM, що розробляється з середини 90-х рокiв унiверситетом Британської Колумбiї (Канада) спiльно з американським iнститутом чавуну i сталi (AISI). Модель не є дуже складною i вибагливою до обчислювальних потужностей у порiвняннi з фiзично обґрунтованими моделями i має задовiльну для багатьох практичних випадкiв точнiсть. Тим не менш, у роботi [6] зазначається, що недолiком цiєї моделi є обмежена здатнiсть до передбачення ефектiв змiни хiмiчного складу сталi на розвиток процесiв, що моделюються. Для рiзних марок сталi значення емпiричних параметрiв i сам вид рiвнянь рiзняться доволi сильно. Так розрахунки проведенi для сталей 10ХСНД i 09Г2С за допомогою програми HSMM давали досить низьку точнiсть при порiвняннi з експериментом [6].

1.1.2 Термодинамiка фазових перетворень. Перед тим як перейти до розгляду фiзично обґрунтованих пiдходiв до моделювання кiнетики фазових перетворень слiд розглянути термодинамiчнi аспекти даного питання. Важливiсть їх обумовлена, по-перше, тим, що процес перетворення починається лише тодi, коли система знаходиться при температурi нижчiй за рiвноважну (нижче вiдповiдної лiнiї на дiаграмi стану), по-друге, як буде показане нижче, кiнетичнi рiвняння, що описують швидкiсть зародкоутворення нової фази мiстять значення змiни енергiї Гiббса при заданiй температурi.

Розвиток апарату математичного i комп'ютерного моделювання фiзико-хiмiчних процесiв при фазових переходах в останнi десятилiття зробив можливим виникнення i розвиток обчислювальної термодинамiки як синтезу фiзичної хiмiї i термодинамiки з комп'ютерними технологiями. Цей науковий напрям вже став невiд'ємною частиною дослiджень, що проводяться в областi створення нових сплавiв i розробцi технологiй виготовлення виробiв з них [22].

Iсторично моделi фiзико-хiмiчної термодинамiки у матерiалознавствi пройшли еволюцiю вiд простих (iдеальний розчин) до значно бiльш складних (субрегулярний розчин). В останнi роки зусиллями Scientific Group Thermodata Europe було описано структуру моделi субрегулярного розчину, оброблено великi об'єми експериментальних даних, отриманi кiлькiснi оцiнки параметрiв моделей для багатокомпонентних систем [6,22]. Важливою особливiстю моделi субрегулярних розчинiв є її унiверсальна здатнiсть описати властивостi фаз рiзної фiзичної природи i врахувати вклад магнiтного упорядкування, можливiсть використання її для багатокомпонентних систем з високою концентрацiєю кожного з компонентiв [22]. Теоретичнi термодинамiчнi дослiдження на її основi (в тому числi розрахунок дiаграм стану) отримали назву CALPHAD-метод (скорочення вiд CALculation of PHase Diagrams).

Основнi принципи CALPHAD-методу, що використовується при моделюваннi фазових рiвноваг полягають в математичному описi температурно-концентрацiйної залежностi термодинамiчних потенцiалiв (зазвичай енергiї Гiббса) фаз i пошуку спiльної дотичної екстраплощини (у випадку двокомпонентної системи - прямої) до них. Точки дотику вiдповiдають рiвноважним концентрацiям компонентiв системи у фазах. При цьому у рiвновазi у системi присутнi тiльки тi фази для яких значення сукупностi точок дотику мiнiмальне (для двокомпонентних систем вiдомо як правило натягнутої нитки). Оскiльки абсолютне значення енергiї Гiббса не визначене, то для практичних розрахункiв використовують вiдноснi величину, значення якої вiдраховують вiд ентальпiї iзобарного стандартного стану при 298,15 К i нормальному атмосферному тиску.

Найбiльш простою моделлю властивостей розчину є модель iдеального розчину, для якого при усiх складах i температурах виконується закон Рауля:

(1.17)

де p_i - тиск насиченої пари компонента i над розчином, Па;
- тиск насиченої пари компонента i над чистим компонентом при тiй же температурi, Па; x_i - мольна частка компонента i у розчинi.

Змiна енергiї Гiббса при утвореннi iдеального розчину описується формулою (1.18) [23]:

(1.18)

де R - унiверсальна газова постiйна Дж/моль?К; T - температура, К.

Ентальпiя iдеального розчину дорiвнює нулю.

Модель iдеального розчину є простою i не потребує додаткових параметрiв. В реальностi iснує доволi мало систем, якi задовiльно можуть бути описанi цiєю моделлю, особливо це стосується твердих розчинiв i багатокомпонентних систем. Але iдеальнiй розчин є нульовим наближенням i основою для бiльш складних моделей, для яких вводять поняття надлишкової енергiї Гiббса, окрiм того, замiсть поняття "мольна частка" компоненту x_i вводиться поняття активностi, що є дещо виправленим значенням концентрацiї, таким чином, щоб закон Рауля виконувався:

(1.19)

де
- коефiцiєнт активностi

Активнiсть може бути вираженою також через вiдносну парцiальну енергiю Гiббса для даного компонента (1.20):

(1.20)

Поширеною моделлю, що описує вiдхилення багатокомпонентного розчину вiд iдеального є модель розбавленого розчину. У рамках даної моделi один iз компонентiв, що мiститься у переважаючiй кiлькостi вважається розчинником. Вплив iнших компонентiв один на одного враховується за допомогою параметрiв взаємодiї для даного розчину [24].

Основна суть методу полягає у розкладеннi надлишкової термодинамiчної функцiї у ряд Тейлора бiля точки, що вiдповiдає чистому розчиннику. Зазвичай обмежуються членами не бiльше другого (рiдше третього порядку). Згiдно з даною моделлю логарифм коефiцiєнту активностi можна розрахувати за формулою (1.21):

(1.21)

Бiльш докладний опис i аналiз рiвнянь, що описують фазовi рiвноваги у рамках CALPHAD-методу i моделi субрегулярного розчину наведенi у роздiлi 2.

Оскiльки CALPHAD-метод потребує досить об'ємних обчислень, в роботах [6, 25] запропонованi емпiричнi залежностi, що описують залежнiсть критичних точок сталi вiд хiмiчного складу i температурну залежнiсть рiвноважних концентрацiй вуглецю в феритi i аустенiтi у сталях рiзного хiмiчного складу.

Для обчислення температури фазової рiвноваги мiж аустенiтом i феритом А₃ за аналогiєю вiдомої формули Кiркалдi [26], використовується вираз виду (1.22):

(1.22)

де ?₃₁ i ?₃₂ - емпiричнi параметри, що є функцiями концентрацiй легуючих елементiв замiщення в сталi; w_C - концентрацiя вуглецю, %.

Для параметрiв ?₃₁ i ?₃₂ методами багатопараметричної оптимiзацiї були отриманi наступнi рiвняння:

?₃₁ = 946,79 - 53,7?w_Mn + 52,07?w_Si + 14,24?w_Si² - 9,20?w_Cr - 49,62?w_Ni +

+ 27,05?w_Mo + 1,72?w_Mo² - (14,22?w_Mn?w_Si + 4,91?w_Mn?w_Si²) (1.23)

?₃₂ = 252,39 - 28,80?w_Mn + 36,72?w_Si + 18,30?w_Si² - 28,31?w_Ni + 19,69?w_Mo +

+ 2.21?w_Mo² - (8,39?w_Mnw_Si + 5,76?w_Mn?w_Si²) (1.24)

Емпiрична формула, що описує залежнiсть температури А₁ вiд складу сталi має дещо простiший вигляд:

А₁ = 726,5 - 21,11?w_Mn + 14,90?w_Si - 8,13?w_Cr -

- 15,88?w_Ni + 3,11?w_Mo - 1,97?w_Mn?w_Si (1.25)

Температурнi залежностi рiвноважних концентрацiй вуглецю у феритi i аустенiтi добре апроксимуються полiномами другого ступеню, що мають вигляд:

C_C? = a_?1 + a_?2?T + a_?3?T² (1.26)

C_C? = a_?1 + a_?2?T + a_?3?T² (1.27)

де a_?1, a_?2, a_?3 та a_?1, a_?2, a_?3 - емпiричнi параметри, що є функцiямi вiд концентрацiй легуючих елементiв замiщення.

Показано [25], що параметри a_?1, a_?2, a_?3 можна виразити через параметри ?₃₁ i ?₃₂, вказанi вище. Отриманi наступнi спiввiдношення:

(1.28)

(1.29)

(1.30)

Для параметрiв, що входять до рiвняння (1.27) отриманi наступнi залежностi вiд хiмiчного складу:

a_?1 = 0,02395 + (- 1,96?w_Mn - 8,29?w_Si + 10,05?w_Cr - 0,87?w_Ni + 8,21?w_Mo)в10^-3 +

+ (- 1,43?w_Mn² + 3,26?w_Si² - 1,29?w_Ni²)в10^-4 (1.31)

a_?2 = (7,1200 + 0,5835?w_Mn + 0,0683?w_Mn² - 1,4545?w_Cr + 0,0180?w_Cr² -

- 0,5186?w_Mo)в10^-5 (1.32)

a_?3 = (- 1,0723 + 0,1875?w_Si - 0,0730?w_Ni + 0,0047?w_Ni²) в10^-7 (1.33)

Аналогiчний полiном другого ступеню використовували i для опису температурної залежностi концентрацiї вуглецю в аустенiтi, рiвноважної з цементитом:

C_C?? = a_?1 + a_?2?T + a_?3?T² (1.34)

Параметри цiєї формули дорiвнюють:

a_?1 = - 0,267 + (0,168?w_Mn + 3,894?w_Si + 1,484?w_Cr)в10^-2 + (0,116?w_Mn² -

- 8,307?w_Si² + 2,36?w_Mn?w_Si²)в10^-3 (1.35)

a_?2 = (3,8190 + 0,0703?w_Mn - 1,2190?w_Si + 0,1378?w_Si² +

+ 0,1460?w_Ni - 0,0040?w_Ni² + 0,2670?w_Mo +

+ 0,0043?w_Mo² - 0,0270?w_Mn?w_Si - 0,0550?w_Mn?w_Si²)в10^-4 (1.36)

a_?3 = (1,4206 + 0,0272?w_Cr)в10^-6 (1.37)

Автори заявляють про доволi високу точнiсть отриманих формул i їх придатнiсть для широкого спектру легованих сталей (в тому числi комплексно легованих багатокомпонентних). Порiвняння розрахованих за ними результатiв з даними наведеними в довiднику [27] показали певну кореляцiю, але досить значна для практичних потреб розбiжнiсть вiдмiчалася для ряду складiв.

Зазначенi формули використовувались нами у комп'ютернiй моделi якостi розрахунку у першому наближеннi, що потiм уточнювалися за допомогою CALPHAD-методу.

Термодинамiка описує лише принципову можливiсть протiкання перетворення, але не дає вiдповiдь про розвиток цього процесу у часi i просторi. Для цього слугує кiнетика.

1.1.3 Моделювання дифузiї у твердих розчинах Кiнетика фазових перетворень, особливо у твердому станi, контролюється насамперед дифузiєю компонентiв. З одного боку - це самодифузiя, що вiдповiдальна за перебудову кристалiчної гратки, з iншого боку розчиннiсть (рiвноважнi концентрацiї) деяких компонентiв сильно вiдрiзняється у фазах мiж якими вiдбувається перехiд, отож потрiбний перерозподiл розчинених компонентiв.

Реальнi сталi i сплави є багатокомпонентними системами, опис дифузiї у якiй є непростою задачею. Теорiя, що кiлькiсно описує залежнiсть коефiцiєнту дифузiї вiд складу твердого розчину викладена в роботах [28-33].

Залежнiсть коефiцiєнту дифузiї вiд температури має вигляд типу рiвняння Аренiусу [28,34] (1.38):

(1.38)

де D₀ - постiйний множник, м²/с; Q - енергiя активацiї дифузiї, Дж/моль

Iснує дуже багато рiзних коефiцiєнтiв дифузiї [35, 36]. Для позначення цих коефiцiєнтiв рiзнi автори використовують рiзну термiнологiю. Запишемо перше рiвняння Фiка для x-компоненти вектора щiльностi дифузiйного потоку атомiв компоненту j_x в наступному виглядi (1.39):

(1.39)

де C_x - об'ємна концентрацiя атомiв компоненту, м^-3; D_x - ефективний коефiцiєнт дифузiї, який ще називають коефiцiєнтом хiмiчної дифузiї [28].

Iстинний коефiцiєнт дифузiї зв'язаний з рухливiстю атомiв M_x вiдомим рiвнянням Ейнштейна (1.40):

(1.40)

Зв'язок мiж зазначеними коефiцiєнтами дифузiї визначається рiвнянням Даркена [35] (1.41):

(1.41)

де ?_x - коефiцiєнт термодинамiчної активностi елементу х, а множник в дужках - термодинамiчний фактор коефiцiєнта дифузiї.

Розчиннiсть вуглецю в феритi i аустенiтi значно вiдрiзняється - рiвноважнi концентрацiї вiдрiзняються на два прядка. Тому у процесi ??? перетворення дифузiйний перерозподiл вуглецю вiдiграє важливу роль.

Згiдно з пiдходом, розвиненим А.А. Смирновим при розрахунку бар'єрiв активацiї мiграцiї атомiв вуглецю використовується статистичний метод середнiх енергiй [35, 36]. Суть методу полягає в тому, що замiсть явного облiку всiх можливих конфiгурацiй атомiв навколо атома, що дифундує, i його енергiй при цих змiнах йому приписується середнє значення потенцiйної енергiї за всiма положеннями того типу, в якому вiн знаходиться. Так, для атомiв вуглецю приймається, що у всiх октаедричних мiжвузлях i перевальних точках вони мають однакову енергiю. Таким чином, сплав замiнюється деяким ефективним чистим металом, в потенцiйному полi якого атом вуглецю має середнi енергiї. Але роботи А.А. Смирнова є чисто теоретичними i не доведенi до кiлькiсного опису i прикладного використання для реальних сплавiв.

Iснує також iнший пiдхiд до розрахунку коефiцiєнтiв дифузiї (дифузiйних рухливостей) атомiв впровадження в сплавах металiв з кубiчною граткою (в тому числi залiза), який є альтернативним пiдходу А.А. Смирнова. Вiн базується на результатах робiт Дж. Агрена та Дж. О. Андерсона [37-39], в яких викладено узагальнений варiант сучасної феноменологiчної теорiї дифузiї в багатокомпонентних системах. Порiвняння двох зазначених пiдходiв у роботi [28] показує, що фiзично вони є еквiвалентними. Дж. Агрен та Дж. О. Андерсон на базi розвиненого ними пiдходу розробили кiлькiсну математичну модель для розрахунку коефiцiєнту дифузiї елементiв впровадження (зокрема вуглецю) в легованому аустенiтi. Дана модель, iнтегрована в комерцiйний програмний пакет DICTRA, але у вiдкритих виданнях вона не опублiкована [28]. При цьому, навiть маючи в своєму розпорядженнi пакет DICTRA, його користувач не має можливiсть застосовувати обговорювану модель для проведення розрахункiв у власних комп'ютерних програмах.

Робота [40] є однiєю з небагатьох, у якiй приводяться кiлькiснi розрахунковi формули для обчислення коефiцiєнту дифузiї у легованому аустенiтi. Приведений у нiй вираз має вигляд (1.42-1.45):

(1.42)

(1.43)

(1.44)

(1.45)

де a_C^? - активнiсть вуглецю в аустенiтi; k_B - постiйна Больцмана; h - постiйна Планка; ?F^* - енергiя активацiї дифузiї вуглецю; Г_m - коефiцiєнт активностi; ? - вiдстань мiж площинами (002) в аустенiтi; ? - молярна доля вуглецю; ?_? - енергiя взаємодiї атомiв вуглецю, розташованих на вiдстанi найближчих сусiдiв.

Наведена вище модель з роботи [40], як зазначається у роботi [28] є дуже неточною. Так згiдно з експериментальними даними з робiт [41-44] розходження з розрахунками становить декiлька разiв (до порядку). При чому, зi зниженням температури вiдхилення розрахунку вiд реальностi зростає. Значна розбiжнiсть з експериментом, в основному, обумовлена тим, що легування змiнює не тiльки термодинамiчний фактор коефiцiєнта дифузiї, але i ефективну енергiю активацiї процесу. Останнiй момент повнiстю iгнорується в обговорюванiй моделi.

Однiєю з найбiльш точних емпiричних формул для розрахунку коефiцiєнту дифузiї вуглецю в аустенiтi наведено в роботах [45, 46]. Вона має вигляд (1.46):

(1.46)

де y_C - концентрацiя вуглецю, що виражена як частка вузлiв пiдґратки впровадження, яка зайнята атомами вуглецю.

Значення емпiричних параметрiв у формулi (1.46) отриманi на базi експериментальних даних роботи [47].

Iснує також цiлий ряд емпiричних формул для обчислення коефiцiєнту дифузiї вуглецю у феритi [28]. Найбiльш поширеними i точними з них є (1.47) з роботи [48]:

(1.47)

i формула (1.48) з роботи [49]:

(1.48)

де Т - абсолютна температура, К

Однак практично усi вiдомi емпiричнi формули для обчислення коефiцiєнту дифузiї не враховують впливу легування, особливо легування елементами замiщення.

Найбiльш точна фiзично обґрунтована модель для розрахунку коефiцiєнту дифузiї в аустенiтi отримана в роботi [28]. Формула має вигляд (1.49):

(1.49)

(1.50)

де u_CC - енергiя взаємодiї атомiв, розташованих в найближчих мiжвузлях (на вiдстанi
, де a - параметр гратки; ?U_С(y_C) - потенцiйний бар'єр активацiї мiграцiї, як функцiя вiд концентрацiї вуглецю; ? - модуль зсуву залiза.

Рiвняння (1.49) може бути розширене для потрiйної системи Fe-C-X, де Х - легуючий елемент замiщення, розчинений в аустенiтi [28, 33]. Такий вираз має вигляд (1.51):

(1.51)

де
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом у пiдгратцi впроваджень решiтки залiза, Дж/моль;
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом у пiдгратцi впроваджень решiтки легуючого елемента, Дж/моль.

Лiнiйна залежнiсть ефективної енергiї активацiї мiграцiї вуглецю вiд його концентрацiї виду
не є просто постульованою, а строго отримана i доведена у роботi [28]. При незмiнному потенцiалi парної взаємодiї атомiв вуглецю лiнiйнiсть концентрацiйної залежностi енергiї активацiї зберiгається при облiку довiльного числа взаємодiючих сусiдiв. Цей момент є важливим з точки зору доцiльностi використання зазначеної лiнiйної залежностi енергiї активацiї вiд концентрацiї вуглецю в математичних моделях.

У роботi [33] вказаний пiдхiд до розрахунку коефiцiєнту дифузiї було розширено на багатокомпонентнi системи з довiльним числом легуючих елементiв. При цьому припускалася адитивнiсть впливу легуючих елементiв замiщення на термодинамiчний фактор i на ефективну енергiю активацiї дифузiї вуглецю. В цьому випадку можна записати наступне рiвняння (1.52) для коефiцiєнту дифузiї:

(1.52)

де D_C0 - предекспоненцiальний множник, що залежить вiд параметра кристалiчної гратки i середньої частоти теплових коливань атомiв [33], м²/с,

D_C0 - a²??, де a - параметр гратки, ? - середня частота коливань атомiв; y_C - пiдграткова концентрацiя атомiв вуглецю; y_S - пiдграткова концентрацiя атомiв легуючого елемента;
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом в пiдгратцi впроваджень решiтки залiза, Дж/моль;
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом в пiдгратцi впроваджень решiтки легуючого елемента, Дж/моль; ? - параметр, що визначає зв'язок мiж ентропiєю i енергiєю активацiї мiграцiї [28], К^-1,
- енергетичний бар'єр активацiї мiграцiї вуглецю в залiзi без легування як функцiя концентрацiї вуглецю [28], Дж/моль: ?_S i ?_S - параметри впливу елементiв на бар'єр активацiї мiграцiї атомiв вуглецю, Дж/моль.

Наведена формула на даний час є однiєю з найбiльш точних [28].

Формула для розрахунку коефiцiєнту дифузiї вуглецю у феритi, беручи до уваги вкрай низьку рiвноважну концентрацiю вуглецю у ньому, має дещо простiший вигляд (1.53) [28]:

(1.53)

де сукупнiсть параметрiв ?_X...?_Z визначає залежнiсть розглянутого коефiцiєнта дифузiї вiд вмiсту легуючих елементiв замiщення.

Кiлькiснi значення параметрiв моделей (1.52 i 1.53) були експериментально вiдмiренi i обчисленi у роботах [28, 47, 50].

1.1.4 Фiзично обґрунтованi моделi розпаду аустенiту У фiзично обґрунтованих моделях розглядаються процеси зародження i зростання фаз - продуктiв розпаду аустенiту, якi описуються на основi рiвнянь математичної фiзики. При цьому максимально використовуються достовiрнi експериментальнi данi.

Утворення фериту стає термодинамiчно вигiдним коли термодинамiчна рухова сила формування фериту стає рiвною рiзницi енергiй Гiббса фериту i аустенiту i менше нуля. Але розрахунок рухової сили, особливо у багатокомпонентних системах, зазвичай виконується в той чи iншiй ступенi наближення. Розрiзняють три ступеня наближення: повна рiвновага (equilibrium) - атоми всiх легуючих елементiв замiщення встигають перерозподiлитися мiж аустенiтом i феритом; орторiвновага (ortoequilibrium) - має мiсце тiльки перерозподiл легуючих елементiв впровадження (зазвичай вуглецю та якого-небудь iншого елементу замiщення); парарiвновага (paraequilibrium) - перерозподiляються атоми тiльки одного елемента впровадження (зазвичай вуглецю).

У бiльшостi фiзичних моделей для опису розпаду аустенiту в умовах безперервного охолодження використовується наближення парарiвноваги. Такий пiдхiд є виправданим, тому як атоми легуючих елементiв замiщення мають значно меншу дифузiйну рухливiсть у порiвняннi з атомами вуглецю.

Розглядають декiлька мод зародження фериту: вершини, ребра, гранi i тiло зерна. Для спрощення розрахункiв зерна фериту апроксимують полiедрами однакової форми i розмiру. При цьому форма полiедру має бути такою, щоб їм можна було щiльно замостити об'єм. Таким є тетраедр, куб, ромбододекаедр та усiчений октаедр. Найбiльш точно аустенiтне зерно апроксимується усiченим октаедром [51]. В такому разi на одне зерно припадає 5 першин, 12 ребер i 7 граней.

При розрахунках швидкостi зародження фериту використовується рiвняння виду (1.54) з роботи [52] та його модифiкацiї:

(1.54)

де D_N - коефiцiєнт дифузiї, що вiдноситься до процесу, що лiмiтує зародження (зазвичай - коефiцiєнт дифузiї вуглецю в аустенiтi); K_PF, A_PF - параметри, що залежать вiд мiсць зародження i форми зародкiв; ?_?? - ефективна питома енергiя границi роздiлу фаз.

Приклади модифiкацiй рiвняння (1.54) можна зустрiти в роботах [6, 11, 53]. Згiдно роботи [6] воно має вигляд (1.55):

(1.55)

де С_k - емпiричний множник, фактор мiсця зародження;
- об'ємна щiльнiсть потенцiйних мiсць зародження;
- енергiя активацiї перебудови гратки; ?_k - ефективна поверхнева енергiя зародку фериту;
- термодинамiчна рухаюча сила ??? перетворення.

Перша експонента з рiвняння (1.54) представляє собою температурну залежнiсть коефiцiєнту самодифузiї. Так згiдно з уявленнями з роботи [6], зародження фериту лiмiтується саме перебудовою гратки. Температурною залежнiстю передекспоненту знехтували. Передекспонент С увiбрав у себе всi константнi величини.

Згiдно з роботою [11] зародження фериту пiдчас розпаду аустенiту описується формулою (1.56):

(1.56)

де N_S - об'ємна щiльнiсть потенцiйних мiсць зародження; Q_N - енергiя активацiї дифузiйного процесу перебудови кристалiчної гратки, Дж/моль; ?G_V - термодинамiчна рушiйна сила перетворення, Дж/м³; ?_eff - питома поверхнева енергiя зародку.

Врахування параметру K_i у формулi (1.56) дозволяє врахувати рiзницi у енергетичному бар'єрi утворення критичного зародку в залежностi вiд мiсця (вершини, ребра, гранi, або тiло зерна). Значення поверхневої енергiї також може змiнюватись за рахунок формування зернограничних сегрегацiй атомiв легуючих елементiв i домiшок [11]. Але у тiй роботi значення Q_N приймали фiксованим.

Пiдчас феритного перетворення вiдбувається ряд процесiв, що мають вплив на нього: дифузiя атомiв легуючих елементiв, перебудова кристалiчної гратки, дифузiя атомiв вуглецю. Звичайно у моделях в якостi лiмiтуючих факторiв феритного перетворення розглядають процеси дифузiйного перерозподiлу вуглецю i перебудову кристалiчної гратки [19, 54-57]. Такi моделi називають mixed mode models.

Для опису швидкостi зростання фериту, що контролюється дифузiєю вуглецю, використовують рiвняння параболiчного росту (1.57) [58]:

(1.57)

де D_C - коефiцiєнт об'ємної дифузiї вуглецю; ? - параметр параболiчного зростання.

Для швидкостi перемiщення мiжфазної границi, що контролюється перебудовою кристалiчної гратки, використовують рiвняння виду (1.58, 1.59) [59]:

(1.58)

(1.59)

де Q^* - енергiя активацiї перебудови кристалiчної гратки (дорiвнює приблизно 140000 Дж/моль).

У роботi [53] наводиться емпiрична залежнiсть енергiї активацiї перебудови кристалiчної гратки при ??? перетвореннi вiд хiмiчного складу аустенiту. Дана залежнiсть має вигляд (1.60):

(1.60)

де y_x - концентрацiя елемента x як доля зайнятих вузлiв у вiдповiднiй пiдргатцi.

Як вiдмiчається у роботi [6] зараз розповсюдження набувають моделi, у яких одночасно розглядаються обидва лiмiтуючи процеси. Такi моделi в англомовнiй лiтературi називають mixed mode models. В зазначених моделях вводиться поняття про ефективне значення концентрацiї вуглецю на мiжфазнiй границi, яке забезпечує рiвнiсть швидкостей її перемiщення за рахунок обох факторiв: дифузiйного вiдтоку вуглецю i перебудови гратки. Вказана концентрацiя вуглецю (iнтефейсна концентрацiя) знаходиться у межах вiд поточної концентрацiї вуглецю в серединi аустенiтного зерна до рiвноважної концентрацiї вуглецю при данiй температурi.

Зародження перлiту в евтектоїдних сталях вiдбувається на границях зерен аустенiту. У низько- i середньо вуглецевих сталях воно починається у мiжфазних областях, що збагаченi вуглецем. В роботi [60] для опису швидкостi зародження перлiтних колонiй використовується вираз (1.61):

(1.61)

де N - щiльнiсть мiсць зародження; ? = k_B?T/h - частотний фактор; Q - енергiя активацiї дифузiї вiдповiдних атомiв через мiж фазну границю; ?G^* - термодинамiчний бар'єр зародження.

Лiмiтуючим процесом при зростаннi перлiтної колонiї є об'ємна дифузiя вуглецю в аустенiтi [6, 53]. Виходячи з даного положення, рiвняння для швидкостi росту перлiту має вигляд (1.62), представлений у роботi [61]:

(1.62)

де S - вiдстань мiж ламелями, що дорiвнює сумi товщин пластин фериту S_? i цементиту S_?; S₀ - критична вiдстань, для якої, згiдно з роботою [57] можна записати:

(1.63)

У роботах [62, 63] розвинуто пiдхiд при якому у якостi лiмiтуючого процесу розглядається дифузiя вздовж мiжфазної границi. Наприклад, у роботi [63] при моделюваннi перлiтного перетворення для сталi з високим вмiстом марганцю у якостi лiмiтуючого процесу дифузiя атомiв марганцю у границi зерен. Рiвняння для швидкостi в цьому випадку записується у виглядi (1.64):

(1.64)

де K_P - коефiцiєнт зернограничної сегрегацiї марганцю;
- коефiцiєнт зернограничної дифузiї атомiв марганцю; ? - товщина мiжфазної границi;
i
- рiвноважнi концентрацiї марганцю на вiдповiдних границях роздiлу фаз;
- середнiй вмiст марганцю в аустенiтi.

В деяких моделях нехтується описом процесу зародження перлiту, тому як вважається, що вiн вiдбувається досить швидко [6, 53, 64].

Зростають перлiтнi колонiї зi швидкiстю, що контролюється дифузiєю вуглецю [6]. При цьому провiдною фазою є цементит [61]. Тому моделювання зростання перлiтної колонiї зводиться до опису росту цементитної пластини у глибину зерна аустенiту.

Найбiльш складним для моделювання є бейнiтне перетворення. Його фiзична природа до кiнця не вивчена i є предметом дискусiй. Воно є дифузiйним i зсувним одночасно. Роботи [10, 65, 66] моделюють його як у першу чергу дифузiйне, тодi як у роботах [67-70] його вважають в основному зсувним.

Для змiни енергiї Гiбса при протiканнi бейнiтного перетворення у роботi [6] наводиться вираз (1.65):

G_N = 3.637?(T - 273.15) - 2540 (Дж/моль) (1.65)

У дифузiйних моделях швидкiсть зародження бейнiтних пластин розраховується з використанням рiвняння (1.66), що наводить автор роботи [6]:

(1.66)

де K - емпiричний параметр; Q - енергiя активацiї процесу, що контролюється дифузiєю; ?G^* - термодинамiчний бар'єр зародження.

У роботi [6] спираючись на експериментальнi данi про бейнiтне перетворення у сталях рiзного складу знайдено емпiричну залежнiсть ефективної енергiї активацiї зародження бейнiтних елементiв вiд концентрацiї легуючих елементiв в аустенiтi. Залежнiсть має вигляд (1.67):

Q_B = 4000 + 28000?y_C + 24000? y_Mn + 58000?y_Mo + 31000?y_Cr (Дж/моль) (1.67)

Для опису зростання бейнiтних елементiв, що мають вигляд пластин, по дифузiйному механiзму у роботi [71] використано наступний вираз (1.68):

(1.68)

де ?_С - радiус вершини бейнiтної пластини, ?_* - параметр, що залежить вiд концентрацiї вуглецю у фазах.

Радiус вершини бейнiтної пластини розраховується за формулою (1.69):

(1.69)

Для розрахунку параметру ?_* наводяться наступнi формули:

(1.70)

(1.71)

У зсувних моделях бейнiтного перетворення нехтується процесом зростання бейнiтних елементiв. Процес перетворення описується як зародження субелементiв, з яких складаються бейнiтнi пластини. Тобто кiнетика процесу визначається кiнетикою зародження субелементiв, якi по зсувному механiзму швидко (майже миттєво) досягають певного розмiру [6]. При цьому видiляють рiзнi типи субелементiв - первиннi (зароджуються на границях зерен i фрагментiв) i автокаталiтичнi (зароджуються на поверхнi iснуючих бейнiтних елементiв).

1.1.5 Врахування впливу деформацiї. Деформацiя аустенiту прискорює процес його розпаду i призводить до значного подрiбнення кiнцевої мiкроструктури [72]. Причиною ефекту прискорення розпаду є прискорення зародження зерен фериту по границях зерен аустенiту [73] та стимуляцiя додаткового зарождення на деформованiй субструктурi всерединi аустенiтних зерен [73]. У iснуючих моделях феритного перетворення вплив деформацiї враховується за допомогою змiни числа мiсць зародження i збiльшення рушiвної сили процесу за рахунок енергiї деформацiї.

Робiт, що фiзично обґрунтовано описують вплив попередньої деформацiї на розпад аустенiту доволi небагато. Як показують експериментальнi дослiдження впливу пластичної деформацiї аустенiту на утворення фериту, проведенi у роботi [72], у деформованому аустенiтi суттєво прискорюється зародження феритних зерен на вихiдних аустенiтних границях. Аналiз, проведений у роботi [74], показав, що цей ефект неможливо пояснити просто збiльшенням числа потенцiйних мiсць зародження на границях. Характер кривих перетворення вдається вiдтворити тiльки при значному зниженнi бар'єра для зародження. При цьому видається, що збiльшення рушiйної сили перетворення (змiни енергiї Гiббса) за рахунок запасеної енергiї деформацiйної субструктури аустенiту занадто мало для забезпечення прискорення зародження, у тiй мiрi, як воно спостерiгається в експериментi [72]. В роботi [11] автори вважають, що зниження бар'єра зародження пов'язано з пiдвищенням енергiї самих границь за рахунок пiдвищення ступеня їх дефектностi i формуванням приграничної деформацiйної субструктури. Даний ефект описують за рахунок введення фактора форми, що залежить вiд ступеня деформацiї наступним чином:

(1.72)

де добуток деформуючої напруги ? на ступiнь деформацiї ? взято у якостi мiри енергiї деформацiї; K_i - фактор форми без урахування деформацiї; q - емпiричний параметр.

Для розрахунку деформуючої напруги при гарячiй деформацiї у роботi [75] отримане емпiричне рiвняння (1.72):

(1.73)

де d_? - розмiр зерна аустенiту, мкм; ? - iстина деформацiя; T_? - температура деформацiї, К; Nb - вмiст нiобiю у твердому розчинi, %.

Для першої моди процесу зародження число потенцiйних мiсць зародження (вершин зерен) не змiнюється. Для другої моди з'являються додатковi мiсця зародження: згiдно даним роботи [11], це мiсця змикання границi зерна з границями субзерен. Враховуючи, що розмiр субзерна зворотно пропорцiйний деформуючому напруженню ?, можна записати [76]:

(1.74)

де k_? - калiбрувальний параметр.

Згiдно з результатами роботи [11], значення емпiричних параметрiв з формул (1.72) та (1.74), що мають вiдношення до зародження на вихiдних границях зерен аустенiта, дорiвнюють вiдповiдно: q_? = 0,0025; k_? = 0,025.

На вiдмiну вiд стимульованого деформацiєю прискорення зародження на вихiдних границях зерен, зародження всерединi зерен, згiдно з роботою [74], спостерiгається тiльки пiсля деякого критичного ступеня деформацiї.

Автори роботи [11] зв'язують цей факт з тим, що у деформованiй субструктурi аустенiту мiсцями зародження енергетично вигiдне, є дiлянки великокутових границь деформацiйного походження. Тому швидкiсть зародження пропорцiйна питомiй площинi поверхнi дiлянок S_HA, яка, в свою чергу, пропорцiйна питомiй площинi поверхнi субзерен (величина, зворотна середньому розмiру субзерна d_SG) i частцi великокутових границь ?_HA.

Тодi для параметра S_HA можна записати:

(1.75)

Iснує спiввiдношення мiж деформуючим напруженням i розмiром субзерна, що було пiдтверджено експериментально [11]. Воно задається формулою (1.76):

(1.76)

де ? - безрозмiрний коефiцiєнт; M - фактор Тейлора; ? - модуль зсуву; b - модуль вектора Бюргерса; ? - деформуюче напруження.

Для оцiнки залежностi частки великокутових границь фрагментiв ?_HA вiд ступеня деформацiї запропоноване рiвняння (1.77):

(1.77)

де b(T) та n - емпiричнi параметри.

В роботi [77] було показано, що параметр b(T) залежить вiд температури вiдповiдно формули (1.78):

(1.78)

Там же було показано, що n = 3.

Швидкiсть зародження фериту всерединi аустенiтних зерен визначається рiвнянням, аналогiчним до наведеної ранiше формули (1.56). Об'ємна щiльнiсть потенцiйних мiсць зародження N_s3 в цьому випадку буде визничатися наступним чином:

(1.79)

де ?_HA - частки великокутових границь (визначається формулою 1.77); ? - деформуюча напруга, a - параметр кристалiчної гратки.

Фактор форми K₃ - у рiвняннi (1.56), що характеризує великокутовi участки границь фрагментiв, мало залежить вiд ступеня деформацiї i, згiдно з результатами роботи [11] дорiвнює 1,20.

1.2 Теорiя i базовi фiзичнi процеси, що лежать у основi деформацiйно-термiчної обробки низьколегованих сталей

1.2.1 Процеси структуроутворення при гарячiй деформацiї Нормальне зростання зерна аустенiту є одним з важливих процесiв, що визначають його мiкроструктуру, що формується при гарячiй деформацiї сталi. Рiст зерна має мiсце пiдчас нагрiвання заготiвлi перед деформацiєю (прокаткою, куванням, штамповкою). Окрiм того, як вiдмiчається в роботi [78], даний процес може активно розвиватися в паузах мiж рiзними етапами деформацiї, коли метал ще має достатньо високу температуру.

Найбiльш часто для опису кiнетики зростання зерна в iзотермiчних умовах використовують рiвняння виду (1.80):

(1.80)

де D_? - розмiр зерна в момент часу t; D_?0 - початковий розмiр зерна аустенiту; Q_GG - ефективна енергiя активацiї процесу; A i n - емпiричнi параметри.

Практика використання рiвняння (1.80) для аналiзу експериментальних даних для рiзних матерiалiв показує, що величина параметру n суттєво залежить вiд природи матерiалу i змiнюється у дiапазонi вiд 2 до 10 [79]. При цьому параболiчний рiст (n = 2), вперше показаний у роботi [78], спостерiгається тiльки у випадку дуже чистих металiв [79, 80].

Великi значення n i їх залежнiсть вiд температури зв'язують з ефектом гальмування руху границь зерен часточками фазових видiлень та ефектом твердорозчинного гальмування атомами домiшок i легуючих елементiв [81]. У зв'язку з цим ефективне значення енергiї активацiї, що отримують при використаннi рiвняння (1.80) на думку автора роботи [78] не мають певного фiзичного сенсу. Для аустенiту значення цiєї енергiї змiнюються у широких межах в залежностi вiд хiмiчного складу сталi i температурного iнтервалу, в якому аналiзується рiст зерна [82]. У роботах [83-85] енергiя Q_GG є пiдгiнним параметром [78].

В роботi [83] здiйснена спроба побудови простої математичної моделi для опису кiнетики зростання зерна в залежностi вiд температури i хiмiчного складу сталi. Запропоноване в результатi рiвняння має вигляд (1.81 - 1.82):

(1.81)

(1.82)

де D_? - розмiр зерна, мкм; Q(X_AE) - ефективна енергiя активацiї процесу; X_AE - вмiст легуючих елементiв, масс. %.

Величина параметру n близька до 4, що, можливо свiдчить про значний ефект гальмування границь зерен атомами легуючих елементiв у твердому розчинi. Автор роботи [78] виказує сумнiв щодо адекватностi формули (1.82) i вiдмiчає невисоку точнiсть i узгодженiсть з експериментальними даними результатiв, отриманих за допомогою рiвняння (1.81).

Формула, схожа з рiвнянням (1.81) використовувалася у роботi [84] для дослiдження впливу мiкролегування титаном на рiст зерна у сталi. Формула має наступний вигляд:

(1.83)

де f та r - вiдповiдно, об'ємна частка i середнiй радiус частинок нiтриду титану.

Наведене рiвняння (1.83) враховує ефект гальмування зростання зерен частинками нiтриду титану. У роботi [78] стверджується, що результати отриманi за рiвнянням (1.83) добре узгоджуються з експериментом.

Рiвняння для опису зростання зерна аустенiту, наведене у роботi [86] має наступний вигляд:

(1.84)

Автори стверджують, що рiвняння (1.84) дає результати, що добре узгоджуються з експериментом для сталi наступного складу: C - 0,99 %, Si - 0,24 %, Mn - 0,31 %, Cr - 1,44 %, Ni - 0,05 %, Cu - 0,12 %, Mo - 0,02 %. Про достовiрнiсть отриманих за формулою (1.84) результатiв для iнших сталей даних немає.

У роботi [87] запропоновано вiдносно просту модель для розрахунку швидкостi росту зерна:

(1.85)

де Q - ефективна енергiя активацiї процесу, значення якої прийнято рiвним 330 кДж/моль; M₀, ?_GB, P - емпiричнi параметри.

Рiвняння, подiбне до (1.85) також було запропоновано i у роботi [78]. Воно має наступний вигляд:

(1.86)

де f, r - вiдповiдно, об'ємна частка i середнiй розмiр частинок карбiдiв i карбонiтридiв.

Таким чином, можна зробити висновок, що емпiричний параметр P з рiвняння (1.85), спираючись на результатi роботи [78] слiд iнтерпретувати як фактор впливу дисперсних частинок на гальмування зростання зерна. Також, слiд звернути увагу, що не дивлячись на рiзнi склади сталей у роботах [78] i [87], в них були отриманi однаковi значення енергiї активацiї Q = 330 кДж/моль. Це очевидно свiдчить про незначний вплив хiмiчного складу сталi на енергiю активацiї процесу росту аустенiтного зерна. Тим не менш, у роботi [85] вiдмiчають її залежнiсть вiд вмiсту у сталi вуглецю.

Вiдомо, що динамiчна рекристалiзацiя розвивається в процесi деформацiї матерiалу. У зв'язку з цим, для цього виду рекристалiзацiї потрiбнi високi температури i низька швидкiсть деформацiї. Для початку динамiчної рекристалiзацiї необхiдна критична ступiнь деформацiї, ?_с, величина якої залежить вiд температури, швидкостi деформацiї i хiмiчного складу сталi. У процесах гарячої прокатки даний вид рекристалiзацiї можливий на її чорновiй стадiї (у чорнових клiтях), що характеризується максимальною температурою i низькими швидкостями деформацiї [78].

Метадинамiчна (або постдинамiчна) рекристалiзацiя характеризується тим, що динамiчна рекристалiзацiя, що почалася при недостатньо високому ступенi деформацiї, проходить не до кiнця, а матерiал остаточно рекристалiзується в процесi пiслядеформацiйної витримки. Вказаний вид рекристалiзацiї суттєво вiдрiзняється вiд статичної в силу того, що вiдразу пiсля деформацiї у матерiалi вже мiстяться сформованi зародки рекристалiзованих зерен, якi в подальшому можуть зростати, забезпечуючи завершення процесу.

Динамiчна рекристалiзацiя супроводжується сильним зниженням мiцностi деформованого матерiалу. ЇЇ розвиток приводить до характерної форми кривих пластичного плину, що мають вираженi пiки [78]. Формування первинних зародкiв динамiчно рекристалiзованих зерен вiдбувається на границях вихiдних зерен аустенiту. Цей факт пояснює залежнiсть величини критичної деформацiї вiд розмiру вихiдного зерна.

Для кiлькiсного опису росту частки динамiчно рекристалiзованого об'єму в залежностi вiд деформацiї пiсля досягнення її критичного значення (? > ?_c) в роботах [88 - 92] використовують рiвняння типу Аврамi наступного виду:

(1.87)

де k та n - емпiричнi параметри, значення яких залежать вiд температури, швидкостi деформацiї i хiмiчного складу сталi.

Типове значення параметру n з формули (1.87) для мiкролегованих сталей становить вiд 1 до 2.

Критична деформацiя значно залежить вiд температури, швидкостi деформацiї, хiмiчного складу сталi i величини зерна аустенiту. В роботi [78] вiдмiчається, що ключовим моментом при створеннi дiєвої кiлькiсної моделi динамiчної рекристалiзацiї є розробка рiвнянь для визначення критичної деформацiї. Це потребує наявностi широкої бази експериментальних даних. У бiльшостi робiт величина критичної деформацiї визначається методом диференцiювання кривих пластичного плину, що було вперше запропоновано у роботi [93]. У даному методi визначається напруження ?_c при якому має мiсце перегин на кривiй залежностi деформацiйного змiцнення вiд напруження. Потiм за знайденим значенням критичного напруження на основi вихiдної кривої пластичного плину знаходиться критична деформацiя. Основна проблема використання цього методу полягає в тому, що прояв перегину на кривих може бути обумовленим iнтенсивним динамiчним поверненням, а не початком рекристалiзацiї. Докладно цей метод описаний у роботi [88].

Згiдно з даними роботи [88], навiть при пiковiй деформацiї динамiчна рекристалiзацiя знаходиться на досить раннiй стадiї. Аналогiчне розходження рiвня критичної деформацiї, що отриманий методом диференцiювання кривих пластичного вплину з даними, що отриманi на основi металографiчних дослiджень, вiдмiчається в рядi робiт.

У роботi [78] вказується наявнiсть прямої пропорцiйностi мiж критичною i пiковою деформацiями:

?_c = ???_p (1.88)

де ? - постiйний коефiцiєнт, що може становити вiд 0,75 до 0,90.

Моделей для розрахунку пiкової деформацiї, на основi якої розраховують величину критичної деформацiї є не досить багато. У роботi [78] наводиться рiвняння (1.89):

(1.89)

де D_?0 - початковий розмiр зерна аустенiту; Z - параметр Зiнера-Холломона;
- функцiя хiмiчного складу сталi; p, q - чисельнi параметри.

Для розрахунку параметру Зiнера-Холломона iснує наступне рiвняння (1.90) [78]:

(1.90)

де
- швидкiсть деформацiї; Q_d - ефективна енергiя активацiї процесу деформацiй, що залежить вiд хiмiчного складу.

Iснує ряд робiт, у яких наводяться формули для розрахунку пiкової деформацiї. Наприклад, у роботi [94] спираючись на експериментальнi данi отримано вираз (1.91):

(1.91)

де w_X - вмiст елементу X; D_?0 - розмiр зерна, мкм

У роботi [95] наведено дещо iншi формули (1.92, 1.93):

(1.92)

(1.93)

де
- ефективний вмiст Nb, з поправкою на вмiст Ti.

Також у данiй роботi було отримано емпiричну залежнiсть (1.94) енергiї активацiї деформацiї вiд хiмiчного складу сталi. Розрахованi на її основi значення можуть бути використанi у формулi (1.90).

(кДж/моль) (1.94)

Однак невелика база вихiдних даних знижує надiйнiсть вищенаведених емпiричних залежностей.

Масштабнi системнi експериментальнi дослiдження динамiчної рекристалiзацiї проведенi в роботах [96 - 98]. Для розрахунку частки рекристалiзованого об'єму використано вираз (1.95):

(1.95)

де k, m - емпiричнi параметри моделi, що залежать вiд температури, швидкостi деформацiї i хiмiчного складу сталi. Значення параметру ? складає приблизно 0,95.

Для розрахунку параметрiв k i m у роботi [98] запропонованi формули (1.96 i 1.97):

(1.96)

(1.97)

Параметр А залежить вiд хiмiчного складу. Для нього було запропоновано наступну емпiричну залежнiсть (1.98):

(1.98)

Дiаметр рекристалiзованого зерна, з достатньо хорошою точнiстю обчислюється за формулою (1.99) з роботи [98]:

(1.99)

Сукупнiсть процесiв релаксацiйної перебудови мiкроструктури деформованого металу, що передує рекристалiзацiї називають поверненням. Воно не веде до утворення нових ректисталiзованих зерен, але при ньому вiдбувається зниження щiльностi дислокацiй, а також формування дислакоцiйних конфiгурацiй зi зниженою енергiєю [99]. За допомогою фiзично обґрунтованих теоретичних кiлькiсних моделей повернення описане доволi мало. Зокрема у роботi [100] наводяться рiвняння (1.100, 1.101), якi дозволяють описати змiну щiльностi дислокацiй i змiну границi текучостi у ходi процесу повернення. Рiвняння мають вигляд:

(1.100)

де ?_y - границя текучостi; M - фактор Тейлора; ? - модуль зсуву; b - модуль вектора Бюргерса; ?_r - емпiричний параметр ?_r - 0,15.

(1.101)

де U_a - енергiя активацiї процесу повернення; V_a - об'єм повернення; v_d - частота Дебая; E - модуль Юнга.

Пiсля завершення деформацiї в металi можливi процеси статичної рекристалiзацiї [78]. Такий вид рекристалiзацiї розвивається, наприклад, у паузах мiж деформацiями при прокатцi чи куваннi. Зародження нових зерен, як i в бiльшостi випадкiв, в ходi даного процесу має мiсце на дефектах кристалiчної будови (це на сам перед висококутовi границi), поблизу яких в результатi пластичної деформацiї утворюються областi з високими градiєнтами кристалографiчних орiєнтувань [101]. В роботi [102] вiдзначається, що новi зерна зароджуються на границях вихiдних, а їх рiст вiдбувається в сторону зерен з бiльш високою щiльнiстю дислокацiй. При великих деформацiях зародження рекристалiзованих зерен може вiдбуватися також в об'ємi зерен за рахунок формування фрагментованої мiкроструктури [102].

Швидкiсть зростання рекристалiзованих зерен є фактично швидкiстью перемiщення їх границь [101]. Зниження рушiйного тиску рекристалiзацiї за рахунок повернення знижує швидкiсть зростання рекристацiзованих зерен.

Кiнетика статичної рекристалiзацiї найбiльш часто описується з використанням рiвняння (1.102) [78]:

(1.102)

де
- частка рекристалiзованого об'єму; t - час iзотермiчної витримки матерiалу пiсля пластичної деформацiї; t₅₀ - час рекристалiзацiї половини об'єму; n - емпiричний параметр.

Залежнiсть часу, за який вiдбувається рекристалiзацiя половини об'єму, вiд температури параметрiв деформацiї i зерна аустенiту описується рiвнянням (1.103) [103-105]:

(1.103)

де ? - ступiнь деформацiї; v - швидкiсть деформацiї;
- розмiр вихiдного зерна аустенiтна; Q_SRX - ефективна енергiя активацiї процесу; A_SRX, p, q - емпiричнi параметри.

Для значення енергiї активацiї процесу в роботi [105] отримана емпiрична залежнiсть вiд хiмiчного складу, що має наступний вигляд (1.104):

Q_SRX = 148636,8 - 71981,3"w_C + 56537,0"w_Si + 21180,0"w_Mn + 121243,3"w_Mo+

+ 64469,6"w_V + 109731,9"w_Nb (Дж/моль) (1.104)

де w_X - вмiст елементу X (мас %).

У роботах [106 - 108] також видiляють метадинамiчну рекристалiзацiю. Цей її вид зводиться до зростання зародкiв, що утворюються у процесi деформацiї. Метадинамiчна рекристалiзацiя практично не має iнкубацiйного перiоду i протiкає вiдносно швидко. На її кiнетику впливають швидкiсть i температура деформацiї, практично незалежно вiд розмiру зерна [78].

1.2.2 Теорiя утворення карбiдних i канбонiтридних фаз у низьковуглецевих сталях, легованих сильними карбонiтридоутворюючими елементами Поширеною є практика мiкорлегування низьковуглецевих низьколегованих сталей такими елементами як V, Nb, Ti та iнодi Zr. Вони здатнi утворювати дисперснi карбiднi i карбонтриднi фази, якi змiцнюють метал та перешкоджають росту зерен при пiдвищених температурах. Канбонiтриднi i карбiднi фази у сталях не завжди кориснi. Так, змiцнюючий ефект вони будуть надавати в разi видiлення всерединi зерна (а не по межах) i маючи досить невеликий розмiр (не бiльше десяткiв нанометрiв). Проте, встановлено, що наявнiсть малорозчинних частинок надлишкової фази на межах зерен може гальмувати зростання зерна аустенiту при нагрiваннi. Останнє актуально для марок сталей, призначених для цементацiї, наприклад 18ХГТ.

У роботi [109] (рисунок 1.1) наводиться система графiкiв розчинностi рiзних карбiдiв в аустенiтi в залежностi вiд температури, вмiсту вуглецю i концентрацiї елемента у сталi, з яких видно, що в низьковуглецевих сталях (~ 0,1% С) з низьким вмiстом ванадiю карбiд ванадiю досить добре розчинний в аустенiтi i його видiлення можливо тiльки при вмiстi ванадiю бiльше 0,08%. Титан i нiобiй бiльшою мiрою схильнi до видiлення карбiдiв з аустенiту при високих температурах. Це корелює з теоретичними розрахунками з робiт [110-113].

Рисунок 1.1 Розчиннiсть карбiдiв ванадiю, нiобiю, титану i цирконiю в

аустенiтi при рiзних температурах в залежностi вiд вмiсту вуглецю

(вказано в % на кривих) в сталi [109]

Так, навiть при вмiстi Ti i Nb бiля 0,01 % можливе видiлення їх карбiдiв при температурах нижче 1000ЊC. Видiлення карбiду цирконiю до початку евтектоїдниого перетворення в низьковуглецевих сталях можливо при вмiстi цирконiю бiльше 0,02%. Ця цифра менше, нiж вiдповiдна для ванадiю.

Розчиннiсть нiтриду нiобiю на пiдставi експериментальних даних, наведених в роботi [114] може бути описана графiком, що представлено на рисунку 1.2. Кривi 1 i 2 отриманi незалежно рiзними експериментальними методами.

Nb, %

Рисунок 1.2 - Розчиннiсть нiтриду нiобiю в ?-Fe [114]

На думку авторiв [114] криву 1 на рисунку 1.2 (данi електронно-мiкроскопiчного дослiдження) можна вважати найбiльш бiльш достовiрною. На пiдставi даних цiєї роботи про систему "залiзо - карбiд нiобiю" можна зробити висновок про те, що максимальна розчиннiсть карбiду нiобiю в залiзi досягається при температурi 1450 ЊC i становить близько 2% (по масi). При - 930 ЊC (безвуглецева система) вiдбувається перитектоїдна реакцiя, в результатi якої вiдбувається утворення ?-Fe залiза. Розчиннiсть карбiду нiобiю у ?-Fe при цiй температурi становить близько 0,05 %, i знижується при охолодженнi. Таким чином, нiтрид нiобiю в значно меншому ступенi розчинний в залiзi, нiж карбiд нiобiю. Тим не менш, згiдно з розрахунками за методикою, розробленою на роботах [115, 116], навiть при незначному вмiстi вуглецю нiобiй з бiльшою iмовiрнiстю утворює карбiд нiж нiтрид. Перевага у видiленнi нiтридних фаз на базi нiобiю спостерiгається при досить високому вмiстi азоту в сталi (бiльше 0,025...0,030%). Мiкролегованi нiобiєм i азотом низьковуглецевi сталi мiстять близько 0,03 % нiобiю. З аналiзу ходу кривої 1 на рисунку 1.2, то можна зробити висновок, що такого вмiсту азоту i нiобiю в твердому розчинi буде досить для видiлення нiтридiв при температурах нижче 1100ЊC. Згiдно ж кривої 2, видiлення нiтридiв буде спостерiгатися при температурах нижче 800ЊС. Так як, на думку авторiв [114] крива 1 видається бiльш достовiрною, є пiдстави вважати, що в даному випадку можливе видiлення дисперсних нiтридiв нiобiю при температурах нижче 1000...1100ЊС.

У роботi [117] зазначається, що швидкiсть видiлення карбiдiв в аустенiтi залежить вiд температури. Важливим моментом є те, що дана залежнiсть має екстремальний характер. Так, видiлення карбонитридiв ванадiю найбiльш швидко вiдбувається при 850 ЊC, карбонитридiв нiобiю при 900 - 920 ЊC, карбiду титану при 925 - 950 ЊC. При бiльш низьких температурах iнтенсивнiсть видiлення зменшується за рахунок зниження дифузiйної рухливостi; при пiдвищеннi температури знижується термодинамiчний стимул проходження процесу. Отже, в даному випадку простежується аналогiя з S-образними кривими iзотермiчного розпаду аустенiту.

В роботi [117] також наголошується, що гаряча пластична деформацiя стимулює процес видiлення надлишкових фаз i, тим самим, скорочує час, необхiдний для його початку i закiнчення при данiй температурi. При цьому велика ступiнь деформацiї надає бiльший вплив на швидкiсть видiлення карбонiтрiдних фаз. Так для малоперлiтних сталей з нiобiєм при деформацiї 15% при температурах 900 - 950 ЊC необхiдно 500...800 с, то пiсля деформацiї 50 - 60 % цей час скорочується до 40 с. Також деформацiя пiдвищує щiльнiсть дефектiв кристалiчної структури, що сприяє видiленню дисперсної карбонiтридної фази всерединi зерна (на дефектах), що зазвичай краще, нiж видiлення на границях зерен, як переважно спостерiгається в недеформованому або слабо деформованому металi.

Видiлення карбонiтридiв, переважно Nb на дислокацiях деформованого аустенiта є одним з важливих процесiв, що контролюють структуроутворення сучасних трубних сталей при їх гарячiй прокатцi. Даний процес розвивається при температурах нижче сольвуса вiдповiдного карбонiтриду. Зазвичай утворення цих частинок має мiсце на стадiї чистової прокатки. Воно завдає суттєвого впливу на статичну рекристалiзацiю деформованого аустенiту за рахунок гальмування зростання рекристалiзованих зерен [78]. Гальмуючий вплив зi сторони частинок залежить вiд їх частки i розмiру.

Моделювання еволюцiї системи частинок карбiдних видiлень включає в себе моделювання їх зародження, зростання i коалесценцiю.

Згiдно з класичною теорiєю швидкiсть зародження частинок розраховується по формулi (1.105) [118-122]:

(1.105)

де N_n - об'ємна щiльнiсть потенцiйних мiсць зародження ; Z - фактор Зельдовича, що враховує можливiсть флуктуацiйного розчинення зародкiв; ? - швидкiсть приєднання атомiв до зародку за рахунок дифузiї;
- термодинамiчний бар'єр зародження

Термодинамiчний бар'єр зародження частинок карбiдiв i карбонiтридiв розраховується за формулою (1.106):

(1.106)

де R_C - радiус критичного зародка;
- питома енергiя поверхнi роздiлу частинка / матриця.

Фактор ? визначається формулою (1.107) з роботи [122]:

(1.107)

де D_Me - коефiцiєнт об'ємної дифузiї атомiв легуючого елементу в аустенiтi; X_Me - мольна доля атомiв легуючого елемента у твердому розчинi; a_? - параметр гратки аустенiту.

Згiдно з даними робiт [118, 119] саме дифузiйна рухливiсть легуючого елементу (металу), а не вуглецю або азоту визначає кiнетику процесiв зародження i зростання карбонiтридiв.

Розмiр критичного зародку визначається рiвнянням (1.108):

(1.108)

де
- термодинамiчна рушiйна сила утворення карбонiтриду.

Термодинамiчна рушiйна сила утворення карбонiтриду розраховується за формулою (1.109) [118, 119]:

(Дж / м³) (1.109)

- молярний об'єм крабонiтриду;
та
- фактична та рiвноважна концентрацiя вуглецю у твердому розчинi.

Якщо форму частинок вважати сферичною, швидкiсть змiни їх радiуса визначається диференцiальним рiвнянням (1.110) з роботи [124]:

(1.110)

де
та
- вiдповiдно, фактична i рiвноважна мольнi долi атомiв металу (легуючого елементу) у твердому розчинi;
- концентрацiя атомiв металу в карбонiтридi;
- вiдношення атомних об'ємiв у матрицi i частинцi карбонiтриду; R₀ - мiнiмальний розмiр частинки, що здатна до зростання при заданому пересиченнi твердого розчину.

Мiнiмальний розмiр частинки, що здатна до зростання при заданому пересиченнi твердого розчину R₀ з рiвняння (1.110) визначається за формулою (1.111) з роботи [124]:

(1.111)

де
- атомний об'єм частинки карбонiтриду

Рiвняння (1.105 - 1.111) являють собою основу математичних моделей еволюцiї системи частинок карбонiтридiв, що утворюються при розпадi пересиченого твердого розчину. Переважна бiльшiсть iснуючих моделей для даної задачi вiдрiзняються лише ступенем деталiзацiї опису цiєї еволюцiї [78]. Однiєю з найбiльш вдалих є модель Кампммана-Вагнера, яка базується на чисельному iнтегруваннi системи диференцiйних рiвнянь зародження i зростання частинок видiлень [122]. Але у роботi [78] висловлюється дещо скептичне вiдношення до використання даної моделi саме для карбонiтридних фаз у сталях, що обумовлено, з одного боку, його невисокою обчислювальною швидкiстю, з iншого - вiдсутнiстю надiйних експериментальних даних про розподiл цих частинок за розмiром.

Таким, чином, в даному роздiлi було розглянуто теоретичнi основи i методи емпiричного i фiзично обґрунтованого математичного моделювання основних процесiв, вiдповiдальних за структуроутворення при термiчнiй i деформацiйно-термiчнiй обробцi сталей. Це на сам перед процеси розпаду аустенiту, рекристалiзацiї i видiлення карбiдних i карбонiтридних фаз.

Описанi у роздiлi методи складають основу для побудови комп'ютерних моделей термодинамiки i кiнетики фазових перетворень у комплексно легованих сталях. Фiзично обґрунтованi моделi є доволi гнучкими у сенсi того, що вони не є прив'язанi до вузького класу матерiалiв, але мiстять парадигми, якi прийнятнi для будь-якого матерiалу, у якому може вiдбуватися процес, що даною моделлю описується. Це свiдчить про великий передбачувальний потенцiал таких моделей.

Реалiзацiя моделювання певних фiзичних процесiв дозволяє вiдтворити процеси структуроутворення. Це дає змогу моделювати вплив параметрiв процесiв на кiнцеву структуру матерiалу.

Фiзично обґрунтоване моделювання кiнетики фазових перетворень неможливе без моделювання термодинамiчних аспектiв цих процесiв. Це пов'язано з залежнiстю швидкостi протiкання процесiв вiд значень змiни енергiї Гiббса, а також вiд ступеню переохолодження нижче рiвноважних критичних температур. Термодинамiчнi розрахунки є досить вимогливими щодо обчислювальних потужностей i потребують значно бiльшого часу нiж кiнетичнi. Тому для обрахунку першого наближення можливо використовувати емпiричнi формули, а потiм використовувати бiльш ємнi розрахунки за CALPHAD-методом.

РОЗДIЛ 2

Математична модель розпаду аустенiту в сталi

Рiзноманiття структур сталей i їх властивостей багато в чому обумовлюється процесами розпаду аустенiту (твердого розчину на основi ?-залiза). Основними структурними складовими, що утворюються при цьому є: ферит (твердий розчин на основi ?-залiза), цементит (Fe₃C) та iншi карбiди, перлiт (евтектоїд, що представляє собою дисперсну, часто пластинчату, сумiш фериту i цементиту), бейнiт i мартенсит. Також може спостерiгатися видiлення графiту (в данiй роботi не розглядається) i часткове збереження неперетвореного аустенiту при низьких температурах (залишковий аустенiт). У свою чергу, перерахованi структурнi складовi можуть мати рiзнi пiдтипи i морфологiю i перебувати в рiзних комбiнацiях в кiнцевiй структурi, що також впливає на властивостi матерiалу. Саме процеси розпаду аустенiту з формуванням заданої структури лежать в основi багатьох методiв термiчної i термомеханiчної обробки сталей. На даний момент накопичено великий обсяг експериментальних даних про розпад аустенiту для сталей рiзного складу в рiзних умовах. Але пiдведення теоретичного базису та побудова фiзично-обґрунтованих математичних моделей дозволяє бiльш передбачувано i направлено впливати на формування структур i властивостей матерiалу розробляти i вдосконалювати методи термiчної i термомеханiчної обробки з урахуванням конкретних характеристик хiмiчного складу i вихiдної структури матерiалу не вдаючись до дорогих i тривалих експериментальних дослiджень.

Створена в данiй роботi комп'ютерна модель може бути роздiлена на наступнi складовi (модулi): термодинамiчний модуль, модуль моделювання дифузiйного феритного перетворення, модуль моделювання дифузiйного перлiтного перетворення, модуль, що описує бейнiтне перетворення (включає реалiзацiю моделей формування переважно зсувних мартенсiтоподiбних складових (бейнiтних елементiв), переважання яких характерно для нижнього бейниту, а також ацикулярних феритоподiбних складових i перлiтоподiбних складових, якi мають мiсце в верхньому бейнiтi, модуль мартенситного перетворення (його програмно не винесено в окремий блок, але вiн входить до складу класу головного вирiшувача). Також програма включає в себе додатковi модулi: для зчитування даних з файлу-завдання i баз даних, для збереження файлу з результатами, для емпiричних розрахункiв перших наближень значень, який уточнюються пiсля бiльш точними, але ресурсоємними фiзично обгрунтованими методами, внесення поправок на попередню деформацiю i наклеп аустенiту (за на явностi таких), структури тимчасового зберiгання даних в пам'ятi комп'ютера. Крiм того, створена додаткова невелика програма для складання вибiрок даних з файлу результатiв (набори пар значень) i перекладу i переведення їх в файл MS Excel для подальшого аналiзу. Безпосереднє збереження результатiв вiдразу в файл Excel в ходi моделювання ("на льоту") привело б до iстотного уповiльнення виконання програми. Для реалiзацiї комп'ютерної моделi використанi мови C ++ (переважно) i Python, також для реалiзацiї завдань багатопараметричної оптимiзацiї та чисельного диференцiювання була пiдключена C ++ бiблiотека з вiдкритим вихiдним кодом ALGLIB, в яку нами було внесено незначнi змiни для адаптацiї її функцiй до реалiй вирiшуваних завдань.

2.1 Термодинамiчне моделювання

В основi використаної методики лежить реалiзацiя CALPHAD-методу (Calculation of Phase Diagrams) термодинамiчного моделювання [22], пiдграткової моделi, розробленої Б. Сундманом i Дж. Агреном в роботi [125] iз застосуванням полiномiв Редлiха-Кiстера [22,23] для обчислення надлишкової енергiї змiшування при утвореннi твердих розчинiв [126].

Функцiєю стану системи при iзобарно-iзотермiчних умовах є енергiя Гiббса [22,127]. Згiдно використаним методам, повна мольна енергiя Гiббса G^? для твердого розчину замiщення представляється у виглядi суми [22]:

(2.1)

де x_i - атомна частка компонента i в розчинi,
- енергiя Гiббса чистого компонента i в модифiкацiї ? в гiпотетичному немагнiтному станi,
- iдеальна компонента енергiї змiшування,
- надлишкова енергiя Гiббса,
- поправка на магнiтне впорядкування (iстотна тiльки для феромагнiтних i антиферомагнiтних фаз).

Даннi про
i її температурнi залежностi є в довiдковiй лiтературi i наводяться у виглядi полiномiальних функцiй або таблиць [22, 127]. Iдеальна складова енергiї Гiббса дорiвнює змiнi ентропiї при утвореннi сумiшi, помноженiй на температуру [22]:

(2.2)

Надлишкова енергiя Гiббса
представляється полiномом Редлiха-Кiстера у виглядi [22]:

(2.3)

де J_i,j - параметри взаємодiї мiж компонентами i та j, r - номер (порядок) параметра взаємодiї.

Параметри взаємодiї лiнiйно залежать вiд температури i є довiдковими величинами, при цьому, в розрахунках використовуються лише параметри взаємодiї вiд нульового до другого порядку [22]. Внесок магнiтного впорядкування в енергiю Гiббса враховувався за методом з робiт [22, 127]. Згiдно з даними цих робiт поправка до значення сумарної енергiї Гiббса на магнiтне впорядкування дорiвнює:

(2.4)

де ? = Т/Т*, де Т* - критична температура (температура Кюрi для феромагнетикiв або для антиферомагнетикiв), Т - поточна температура, К; В₀ - середнiй магнiтний момент на один атом, параметр g (?) обчислюється за формулами (2.5, 2.6):

при ? © 1 (2.5)

(2.6)

де p - частка магнiтної ентальпiї, поглиненої вище критичної температури, залежить вiд структури. Для ОЦК p = 0,40 для ГЦК p = 0,28.

Значення температури Кюрi для ?-фази в залежностi вiд хiмiчного складу розраховувалося за емпiричною формулою (2.7) на основi робiт [22, 127]:

(2.7)

де y_i - концентрацiя i-го елементу виражена як вiдсоток вузлiв кристалiчної решiтки у вiдповiднiй пiдгратцi, зайнятих атомами даного елементу.

Значення параметра B₀ для ?-фази визначалося за формулою (2.8) [22]:

(2.8)

Для аустенiту вплив магнiтного впорядкування виражено куди менш сильно, але воно також враховувалося в моделi. Залежнiсть значень T_C i B₀ для ?-фази представлена формулами (2.9, 2.10):

(2.9)

(2.10)

Дещо складнiше виглядає модель для твердого розчину впровадження, який утворюють з залiзом C, N i iншi елементи з малим радiусом атома. Для цих випадкiв застосовується пiдґраткова модель [33], в рамках якої розглядають твердий розчин, як що складається з пiдґраток замiщення i впровадження, елементи якого взаємодiють мiж собою, як всерединi однiєї пiдгратки, так i мiж рiзними пiдгратками [22]. У систему включається ще один компонент - вакансiї вузли пiдґратки не зайнятi атомами.

У ГЦК твердому розчинi на один вузол пiдґратки замiщення iснує одна "пора", тобто позицiя у пiдґраткцi впровадження a = b = 1. Для ОЦК твердого розчину на один вузол пiдґратки замiщення iснують 3 пори a = 1, b = 3. Таким чином, компонентами розчину є атоми введених в нього хiмiчних елементiв i вакансiї. Для проведення розрахункiв в рамках пiдґраткової моделi атомнi частки компонентiв x_i замiнюють на частки вузлiв y_i, зайнятих компонентами в його пiдґратках [33, 127].

Пiдґраткова модель повної енергiї Гiббса для твердих розчинiв має вигляд:

(2.11)

(2.12)

де верхнi iндекси 1 i 2 при y_i i y_j вказують на концентрацiї атомiв компоненту в пiдґратцi замiщення i впровадження, вiдповiдно.

При описi енергiї Гiббса цементиту, його представляють таким, що складається з двох пiдґраток: металевої (Fe з легуючими елементами (Mn, Cr - при їх наявностi)), впровадженими в цементит, i вуглецевої [22]. На один атом металу припадають 3 атома вуглецю. Концентрацiя вуглецю в його пiдґратцi вважається рiвною 1, наявнiстю вакансiй (як наслiдок - вiдхиленнями вiд стехiометрiї) нехтуємо, тому що область гомогенностi цементиту мала. У всiх фазах рiвноважної гетерогенної системи хiмiчнi потенцiали кожного компонента у всiх фазах рiвнi мiж собою. На цiй пiдставi можна скласти незалежнi рiвняння, так як хiмiчний потенцiал одного i того ж компонента в рiзних фазах описується рiзними функцiями концентрацiй i температури. Геометричне вiдображення рiвностi хiмiчних потенцiалiв двокомпонентної системи означає, що знайдено положення загальної дотичнiй до кривих потенцiалiв (концентрацiйної залежностi енергiї Гiббса) наявних в рiвновазi при заданiй температурi фаз. Точки дотику цiєї прямої до кривих потенцiалiв визначають склад фаз, що вiдповiдає стану рiвноваги.

У багатокомпонентних системах (до яких вiдносяться сучаснi легованi сталi) потрiбно вiдшукати положення не прямої, а гiперплощини вiдповiдної розмiрностi, дотичної до багатовимiрних поверхонь, що описують термодинамiчнi потенцiали фаз. Завдання вiдшукання хiмiчного потенцiалу компоненту в багатокомпонентнiй системi при використаннi наведених вище складних моделей температурно-концентрацiйної залежностi енергiї Гiббса може бути вирiшена тiльки чисельно iз застосуванням комп'ютерної технiки. Математичнi методи чисельного рiшення нелiнiйних систем рiвнянь подiбного типу наведенi в роботi [128]. У розробленiй автором (В. В. Каверинським) комп'ютернiй програмi для даного завдання реалiзований спецiальний модуль з пiдключенням бiблiотеки ALGLIB для задач багатопараметричної мiнiмiзацiї нев'язок. При цьому спочатку з використанням емпiричних формул з роботи [25] обчислюються першi грубi наближення, а потiм проводиться уточнення значень. Це iстотно скорочує час обчислень i запобiгає нестiйкостi рiшення або вiдшукання помилкових рiшень, якi не мають фiзичного сенсу.

2.2 Дифузiйна модель феритного перетворення

2.2.1 Зародження фериту. Модуль реалiзацiї даної моделi займає одне з центральних мiсць в нашiй комп'ютерної моделi i є другим за ресурсоємностю пiсля термодинамiчного модуля. Сутнiсть моделi зводиться до опису зародження i росту кристалiв фериту в аустенiтних зернах i дифузiйного перерозподiлу компонентiв мiж фазами.

У моделi припускалося, що розмiр вихiдних аустенiтних зерен однаковий, i вони мають форму усiченого октаедра. Усiченими октаедрами простiр заповнюється без промiжкiв, крiм того, на пiдставi робiт [6], така форма є оптимальною для моделювання. Iснує ряд характерних мiсць зародження фериту: на вершинах, гранях, ребрах i в тiлi зерна. При цьому швидкостi зародження i зростання в значнiй мiрi вiдрiзняються вiд мiсця зародження, але описуються схожими рiвняннями. При цьому до уваги бралися три моди процесу: на вершинах, на ребрах i гранях (ребра не видiлялися як специфiчнi мiсця зародження, що мають скiльки-небудь значнi переваги перед гранями, грунтуючись на даних робiт [6, 53]) i в тiлi зерна. Третя мода (тiло зерна) є незначною при вiдсутностi попереднього наклепу i малої щiльностi дислокацiй [129].

Було прийняте (на пiдставi прийнятої форми усiченого октаедра). Об'єм даного полiедра дорiвнює:

(2.13)

де a - довжина ребра.

Кiлькiсть зерен такої форми в одиницi об'єму дорiвнює:

(2.14)

Як характерний розмiр (d) був прийнятий дiаметр вписаної сфери, яка пов'язана з довжиною ребра усiченого октаедра (a) спiввiдношенням (2.15):

(2.15)

(2.16)

Пiдставляючи (2.16) в (2.14) отримуємо:

(2.17)

При замощеннi простору усiченими октаедрами на одну клiтинку припадає 5 вузлiв (вершин). Отже, кiлькiсть цих вузлiв в одиницi об'єму дорiвнюватиме:

(2.18)

Отже, залежнiсть вiд часу потенцiйної кiлькостi мiсць зародження фериту можна описати формулою (2.19):

(2.19)

де d_? - середнiй характерний розмiр (дiаметр описаної сфери) зерна аустенiту, ?N₁(t) - число зерен фериту, який вже зародилися в вершинах до моменту часу t.

На пiдставi даних робiт [6, 53, 129], враховуючи процес заростання феритом границь зерен аустенiту об'ємна щiльнiсть додаткових мiсць зародження по другiй модi розраховувалася за формулою (2.20):

(2.20)

де a_?(T, x) - параметр гратки аустенiту, як функцiя вiд температури i складу, м, S_?(t) - частка площi границь зерен аустенiту, зайнятої ферритом до моменту часу t.

Залежнiсть параметра гратки аустенiту (у нм) вiд температури i вмiсту вуглецю описувалася, отриманою нами, емпiричною формулою (2.21):

a_?(T, x) = 0,356 + 8,5?10^-6?T+3,3?10^-3?[C,%] (2.21)

де T - температура, К, ?[C,%] - поточний процентний вмiст вуглецю в аустенiтi.

Зародження фериту в тiлi зерна, вiдбувається в основному при наявностi наклепу. У нашiй моделi вважалося, що мiсцями зародження фериту в серединi зерен є переважно границi субзерен, а швидкiсть його зародження залежить вiд розмiру субзерна i частки великокутових границь. Розмiр субзерна оцiнювався за формулою (2.22), отриманою на пiдставi даних робiт [129]

(2.22)

де k_?1 - емпiричний параметр, що враховує релаксацiю напружень на момент перетворення, ? - коефiцiєнт Пуассона, ?(T_?) - модуль зсуву при температурi деформацiї, b - модуль вектора Бюргерса, ?₀ - внутрiшня напруга пiсля деформацiї.

Частка великокутових границь розраховувалася за формулами (2.23, 2.24) з роботи [130]:

(2.23)

(2.24)

де T_? - температура деформацiї.

Рiвень внутрiшнiх напружень пiсля деформацiї оцiнювався за емпiричною формулою (2.25) з роботи [25]:

(2.25)

де ? - ступiнь деформацiї, ? - швидкiсть деформацiї, d_? - розмiр зерна аустенiту, T_? - температура деформацiї.

Вважається, що зародження фериту контролюється переважно термоактивованою перебудовою гратки аустенiту [6]. Для опису швидкостi зародження фериту при розпадi аустенiту в лiтературi [6, 52, 53, 129] є цiлий ряд рiзних, але в цiлому, схожих формул, висхiдних до рiвняння з роботи [52]. На пiдставi наявних даних i звiрки отриманих результатiв з експериментом, для розрахунку швидкостi зародження фериту по першiй i другiй модi в нашiй математичнiй моделi використовувалося рiвняння (2.26):

(2.26)

де J_i - швидкiсть зародження фериту по i-й модi процесу, 1/с?м³; С_i - емпiричний коефiцiєнт, фактор, який враховує вплив ступеня дефектностi кристалiчної структури в характерному мiсцi зародження, на рiвень рухливостi атомiв, ?К^1/2/с?м³;
- кiлькiсть потенцiйних мiсць зародження на поточний момент часу; T - температура, К; Q_N(Y_AE) - енергiя активацiї перебудови кристалiчної гратки аустенiту в гратку фериту, як функцiя хiмiчного складу аустенiту, Дж/моль, R - унiверсальна газова постiйна, Дж/моль?К; K₁(x), K₂(x) - емпiричнi коефiцiєнти, якi виражають поправку значення енергiї зародка фериту на хiмiчний склад (легування) твердого розчину; ?_eff - ефективна поверхнева енергiя зародка фериту (без урахування поправки на мiсце зародження i легування), Дж/м²; k_B - постiйна Больцмана, Дж/К; ?G_???(T, Y_AE) - змiна об'ємної енергiї Гiббса при ??? перетвореннi як функцiя хiмiчного складу i температури, Дж/м³.

Для швидкостi зародження фериту всерединi зерен аустенiту використовувалися подiбнi, але дещо iншi формули: (2.27) - для субзеренного зародження, i (2.28), для симпатичного зародження:

(2.27)

(2.28)

де f_AU(t) - об'ємна частка аустенiту, до даного моменту часу, N₃(t) - кiлькiсть зерен фериту, що зародилися до даного моменту часу, Q_AF(Y_AE) - енергiя перебудови кристалiчної гратки аустенiту в гратку фериту при перетвореннi всерединi зерен, як функцiя хiмiчного складу аустенiту, Дж/моль, Q_AF(Y_AE) ? Q_N(Y_AE), k_P та k_S - поправочнi коефiцiєнти, ?G_???(T, Y_AE) - змiна молярної енергiї Гiббса при ??? перетвореннi як функцiя хiмiчного складу i температури, Дж/моль.

Фiзичний сенс коефiцiєнтiв K₁(x) i K₂(x) неоднозначний. Їх можна розумiти як узагальнену поправку, що враховує вплив хiмiчного складу на значення поверхневої енергiї зародка фериту i на значення змiни енергiї Гiббса з урахуванням надмалого об'єму зародка, деякої вiдмiнностi його кристалiчної структури вiд кристалiчної решiтки макрооб'ємiв фериту i частково зсувного механiзму його зародження. В ходi звiрки з експериментальними даними [131,132], встановлено, що для низьколегованих сталей K₂(x) близький до 1, вiн значущий для нiкелевих сталей i дорiвнює 1 + 0,9" [Ni,%]. Коефiцiєнт K₁(x) значимо залежить вiд марганцю i молiбдену i приблизно дорiвнює k₀ + 0,15"[Mn,%] + 1.0"[Mo,%]. Значення k₀ - це поправка на моду процесу i становить приблизно 0,05 для першої моди i 0,5 для другої. Значення ефективної поверхневої енергiї зародка дорiвнює 0,055 Дж/м². Зазначенi отриманi нами в ходi верифiкацiї моделi, результати близькi до даних вимiряних у роботах [6, 53, 129], що пiдтверджує їх достовiрнiсть. Хоча слiд звернути увагу, що значення енергiї зародження фериту i її залежностi вiд рiзних факторiв є "вузьким" мiсцем моделi i вимагають додаткових експериментальних дослiджень для встановлення бiльш точних i складних залежностей i їх фiзичної iнтерпретацiї. Змiна об'ємної енергiї Гiббса при ??? перетвореннi розраховувалася за ранiше описаним термодинамiчними методами, для обчислення поточних його значень при нерiвноважному вмiстi вуглецю в переохолодженому аустенiтi застосований метод з роботи [133].

У розрахунках використовувалися концентрацiї y_X, якi представляють собою частки вузлiв пiдграток замiщення i впровадження, зайнятих вiдповiдно атомами елементiв замiщення i впровадження. Якщо в якостi елементу впровадження розглядати тiльки вуглець, то концентрацiї y_X, пов'язанi з молярними частками x_X наступним чином: y_X, = x_X,/(1 - x_C).

Енергiя активацiї дифузiйної перебудови решiтки покладалася такою, що дорiвнює енергiї активацiї зерномежевої самодифузiї, що дорiвнює приблизно половинi [53] енергiї активацiї об'ємної самодiфузii в аустенiтi, яка на пiдставi даних роботи [53] описується емпiричною формулою (2.29), Дж/моль:

(2.29)

Значення отриманi за формулою (2.29) узгоджуються з результатами, вимiрюваними в роботi [129], що пiдтверджує її достовiрнiсть i можливiсть застосування для розрахункiв.

2.2.2 Зростання зерен фериту. Зародившись, кристал фериту починає рости. У роботах [6, 53] показано, що головним фактором, що лiмiтує швидкiсть росту фериту є дифузiйний перерозподiл вуглецю мiж аустенiтом i зростаючим феритом. Перерозподiл iнших хiмiчних елементiв мiж зазначеними фазами в ходi перетворення є незначним i їм в моделюваннi можна знехтувати [53], але їх вплив має велике значення на дифузiю вуглецю. Таким чином, моделювання росту фериту багато в чому зводиться до моделювання дифузiї вуглецю в ? i ?-твердих розчинах. Крiм того, слiд враховувати зiткнення зростаючих зерен i спадання об'ємної частки аустенiту в структурi. Другим важливим фактором, що впливає на швидкiсть росту фериту є перебудова кристалiчної гратки [6].

Швидкiсть зростання фериту, контрольована дифузiйним вiдтоком вуглецю для зерна фериту сферичної форми описується рiвнянням (2.30) з роботи [53]:

(2.30)

де
- коефiцiєнт об'ємної дифузiї вуглецю в аустенiт, як функцiя складу i температури, усереднений за профiлем концентрацiї вуглецю, м²/с; R_? - радiус даного зерна фериту, м;
- молярна iнтерфейсна концентрацiя вуглецю з боку аустенiту,
- поточна середня молярна концентрацiя вуглецю всерединi аустенiтного зерна;
- рiвноважна молярна концентрацiя вуглецю в феритi.

Швидкiсть перемiщення ?/?-границi, що контролюється перебудовою решiтки, може бути описана формулою (2.31) з роботи [58]:

(2.31)

де M₀ - параметр рухливостi ?/?-границi, M₀ - 10 м⁴/с?Дж [53]; Y^*_AE - вказує на те, що значення розраховуються для концентрацiй, що мають мiсце безпосередньо в дiлянцi перетворення. Пiдграткова концентрацiя атомiв елементiв в зазначених дiлянках (y^*) покладалася такою, що дорiвнює середньому значеннню мiж iнтерфейсним з боку аустенiту i рiвноважним для фериту значеннями.

Значення iнтерфейсної концентрацiї вуглецю розраховується з умов рiвностi швидкостей росту фериту, отриманим за рiвнянням (2.30) i (2.31), з урахуванням того, що значення iнтерфейсної концентрацiї неявно входить i в рiвняння (2.31). Для обчислення ефективної швидкостi росту використовувалася формула (2.30).

Так як реальна форма зерен є несферичною i має мiсце анiзотропiя їх зростання (особливо на раннiх стадiях) [53] в модель були введенi коригуючi емпiричнi фактори форми, що залежать вiд мiсця зародження.

Теорiя дифузiї вуглецю в багатокомпонентних твердих розчинах (зокрема в легованому аустенiтi i феритi) розвинена в роботах [28, 33]. Виходячи з результатiв цих робiт, можна зробити висновок, що залежнiсть коефiцiєнта об'ємної дифузiї вуглецю вiд хiмiчного складу твердого розчину i температури може бути описана наступним рiвнянням (2.32).

(2.32)

де D_C0 - предекспоненцiальний множник, що залежить вiд параметра кристалiчної гратки i середньої частоти теплових коливань атомiв, м²/с, D_C0-a²??, де a - параметр гратки, ? - середня частота коливань атомiв; y_C - пiдграткова концентрацiя атомiв вуглецю; y_S - пiдграткова концентрацiя атомiв легуючого елемента;
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом в пiдгратцi впроваджень решiтки залiза, Дж/моль;
- залежна вiд температури енергiя взаємодiї атома вуглецю з найближчим до нього вакантним вузлом у пiдгратцi впроваджень решiтки легуючого елемента, Дж/моль; ? - параметр, що визначає зв'язок мiж ентропiєю i енергiєю активацiї мiграцiї, К^-1,
- енергетичний бар'єр активацiї мiграцiї вуглецю в залiзi без легування як функцiя концентрацiї вуглецю, Дж/моль; ?_S i ?_S - параметри впливу елементiв на бар'єр активацiї мiграцiї атомiв вуглецю, Дж/моль.

Згiдно з даними роботи [28] максимальна похибка обчислень за формулою (27) становить приблизно 8 - 10 %. У розробленiй нами програмi враховувався вплив на дифузiю вуглецю наступних елементiв: сам C, Mn, Si, Cr. Вони мiстяться в багатьох сталях, часто в значнiй кiлькостi, а їх вплив на дифузiю вуглецю є iстотним. За результатами цих же робiт, D_C0 змiнюється в межах 1,4...4,5?10^-7 м²/с, а ? складає близько 2,22...2,59?10^-4 К^-1. Залежнiсть енергетичного бар'єру активацiї мiграцiї вуглецю в залiзi вiд вмiсту вуглецю лiнiйна i для випадку аустенiту описується формулою (2.33):

(2.33)

Параметри
по свiй сутi термодинамiчнi i вони ж використовувалися при обчисленнi деяких компонент надлишкової енергiї в термодинамiчнiй моделi. Їх залежностi вiд температури i складу для залiза i легуючих елементiв наведенi нижче (2.34 - 2.38):

(2.34)

(2.35)

(2.36)

При T < 1519 К:

(2.37)

При T > 1519 К:

(38)

Параметри ?_S и ?_S по даним робiт [22, 127, 128] складають:

?_Mn = 21752 Дж/моль; ?_Mn = -506983 Дж/моль;

?_Al = 146612 Дж/моль; ?_Al = -2920093 Дж/моль;

?_W = 2080000 Дж/моль; ?_W = -27820000 Дж/моль;

?_Cr = 1041871 Дж/моль; ?_Cr = -2117897 Дж/моль;

?_Co = -41340 Дж/моль; ?_Co = -1702000 Дж/моль;

Збiльшення об'ємної частки фериту X_?(t) i площi границь зерен аустенiту, покритих феритом S_?(t) описувалися рiвняннями (2.39) та (2.40) з роботи [53].

, (2.39)

де
i
вiдповiдно радiус i швидкiсть росту об'ємiв зерен фериту, що зародилися в момент часу ?; ?_vi - коригувальний фактор форми для i-ї моди процесу;
- швидкiсть зародження зерен фериту в момент часу ? за i-ю модою процесу.

(2.40)

де d_? - розмiр зерна аустенiту;
- фактори анiзотропiї за i-ю модою процесу.

2.3 Модель перлiтного перетворення

Рiвняння моделi, яка описує перлiтне перетворення, в цiлому близькi до таких для феритної моделi. При цьому вважалося, що лiмiтуючим фактором розвитку процесу зростання перлiтної колонiї є зростання цементиту. Вважається, що його зародження вiдбувається в областях з максимальною локальною концентрацiєю вуглецю, якими є областi аустенiту, прилеглi до границi роздiлу фаз. Зародження цементиту вiдбувається досить швидко, так, що його швидкiстю можна знехтувати [6]. Таким чином, кiнетика перлiтного перетворення описується рiвняннями (2.41, 2.42) з роботи [53]:

, (2.41)

, (2.42)

де
- концентрацiя вуглецю на границi роздiлу аустенит/цементит;
- концентрацiя вуглецю в цементитi;
- молярна iнтерфейсна концентрацiя вуглецю з боку аустенiту;
- коефiцiєнт об'ємної дифузiї вуглецю в аустенiт як функцiя складу i температури, усереднений за профiлем концентрацiї вуглецю вiд
до
, м²/с;
- напiвширина мiжпластинової вiдстанi в перлiтi;
- питома енергiя ?/? - границi;
- змiна енергiї Гiббса при видiленнi цементиту з аустенiту.

2.4 Модель бейнiтного перетворення

Бейнiтне перетворення описується трохи iнакше, так як воно вiдбувається по зсувному механiзму i супроводжується частковим дифузiйним перерозподiлом вуглецю. При цьому лiмiтуючим фактором кiнетики процесу є зародження бейнiтних елементiв, зростання їх вiдбувається швидко i часом вiд зародження до виростання до максимального розмiру при моделюваннi можна знехтувати [6, 68]. При цьому межi зерен є непереборною перешкодою для зростання бейнiтного елементу. Зародження їх вiдбувається на ?/? i ?/?-границях, а також на вже наявних бейнiтних елементах.

Вiдповiдно до робiт [6, 68], зародження бейниту стає можливим нижче температури, при якiй змiна енергiї Гiббса ??? перетворення стає нижче деякого значення ?G_sh. Фiзичний сенс ?G_sh не має однозначного трактування, а величина становить ~ 500 Дж/моль. Для розрахунку швидкостi зародження елементiв бейниту використовувалася формула (2.43) з роботи [6]:

(2.43)

де С_k - предекспонент, емпiричний параметр, що залежить вiд моди процесу (мiсця зародження бейнiтного елемента); F_k(t) - параметр, що визначає змiну у часi в мiру розвитку процесу числа мiсць зародження бейнiтних елементiв;
- енергiя активацiї зародження бейнiтних елементiв як функцiя вiд хiмiчного складу аустенiту; k_k - поправка до значень величини змiни енергiї Гiббса при зсувному характерi перетворення в вiдповiдному характерному мiсцi зародження.

При бейнiтному перетвореннi видiляються наступнi моди процесу: на ?/?-границях, на ?/?-межах, вториннi елементи вздовж ?/?-границь, симпатичне зародження на вже наявних бейнiтних елементах. Параметр F_k(t) в залежностi вiд моди процесу обчислюється вiдповiдно за формулами (2.44 - 2.47):

(2.44)

(2.45)

(2.46)

(2.47)

де
- частка границь зерен, що зайнята феритом;
- частка границь зерен, що зайнята бейнiтом;
- розмiр зерна аустанiту, м;
- об'ємна частка продуктiв дифузiйних перетворень;
- об'ємна частка аустенiту.

У моделi передбачалося, що бейнiтний елемент має форму прямокутного паралелепiпеда i з'являється вiдразу заданого розмiру (часом зростання знехтували). Розмiри бейнiтних елементiв обчислювалися за формулою (2.48) з роботи [6]:

(2.48)

де k₁ i k₂ - емпiричнi параметри, рiзнi для поздовжнього i поперечного напрямку; B_S - температура, нижче якої бейнiтне перетворення є можливим; T - температура, при якiй вiдбувається перетворення

Прирiст об'ємної частки бейнiту за малий iнтервал часу dt описується диференцiальним рiвнянням (2.49):

, (2.49)

де S_B - середня площа, що покривається одним бейнiтним елементом.

Прирiст частки границь зерен аустенiту, покритих бейнiтом, описується диференцiальним рiвнянням (2.50):

(2.50)

де S_B - середня площа, що покривається одним бейнiтним елементом.

Прирiст концентрацiї вуглецю в аустенiт при протiканнi бейнiтного перетворення описується рiвнянням (2.51):

, (2.51)

де k_tr - параметр захвату вуглецю у бейнiтi.

Величина параметра k_tr визначається спiввiдношенням часу, необхiдного для повного дифузiйного вiдтоку вуглецю з бейнiтного елемента (?_D), i часу утворення елементiв, якi блокують процес (?_B). Значення параметрiв ?_D i ?_B обчислювалися за формулами (2.52, 2.53):

(2.52)

(2.53)

де w_B - поперечний розмiр бейнiтного елемента, м;
- коефiцiєнт дифузiї вуглецю в феритi, м²/с; k_? - емпiричний коефiцiєнт. Якщо ?_B < ?_D, то k_tr = ?_B / ?_D, в iншому випадку вiн вважався таким, що дорiвнює 1.

2.5. Модель мартенситного перетворення

Мартенситне перетворення (змiна кiлькостi мартенситу при зниженнi температури перетворення переохолодженого аустенiту) описувалося формулами з роботи [134]. Так, згiдно iз зазначеною роботою, частка аустенiту, здатного перейти в мартенсит при заданiй температурi, дорiвнює (2.54):

(2.54)

де M_S - температура початку мартенситного перетворення, що залежить вiд хiмiчного складу аустенiту, К; m, n - залежнi вiд хiмiчного складу параметри [6].

Параметри M_S, m та n обчислюються за формулами (2.55 - 2.57):

M_S = 764,2 - 302,6?[C, %] - 30,6?[Mn, %] - 14,5?[Si, %] - 16,6?[Ni, %] -

- 8,9?[Cr, %] + 2,4?[Mo, %] - 11,3?[Cu, %] (2.55)

m = 0,0231 - 0,0105?[C, %] - 0,0017?[Ni, %] + 0,0074?[Cr, %] - 0,0193?[Mo, %]

(2.56)

n = 1,4304 - 1,1836?[C, %] - 0,7527?[C, %]² - 0,0258?[Ni, %] -

- 0,0737?[Cr, %] + 0,3108?[Mo, %] (2.57)

2.6 Загальнi принципи виконання розрахункiв за розробленою математичною моделлю

Можливiсть протiкання процесу феритного перетворення розглядається моделлю за умови, якщо температура системи нижче A₃, рiвновагу мiж аустенiтом i феритом не було досягнено, перлiтне перетворення не розпочалося. Умовами завершення моделювання феритного перетворення можуть бути: досягнення спiввiдношення фаз ферит/аустенiт близького до рiвноважного (тiльки за умови подальшого не виведення системи з рiвноваги), початок перлiтного перетворення, досягнення умовного штучного критерiю зупинення розрахунку по температурi або лiмiту часу (останнє стосується i всiх iнших перетворень). Перлiтне i феритне перетворення протiкати одночасно не можуть. Перлiтне перетворення починає прийматися до розгляду нижче температури A₁ при досягненнi концентрацiї вуглецю в аустенiтi не менше необхiдної для утворення перлiту при данiй температурi. Критерiями завершення моделювання перлiтного перетворення можуть бути: повне (або майже повне) завершення перетворення аустенiту, досягнення штучних лiмiтiв по температурi або часу. В ходi моделювання визначається мiжпластiнчаста вiдстань в перлiтi. При значеннях розрахованої мiжпластиночної вiдстанi менше 0,4 мкм структури вiдносили до сорбiту та трооститу. При бiльших - вважали перлiтом. Критерiєм можливостi протiкання бейнiтного перетворення є досягнення значення змiни енергiї Гiббса ??? перетворення нижче ?G_sh. ~ 500 Дж/моль. При цьому, однак, не виключається формування фериту (якщо не почалося формування перлiту). Цей ферит вважався ацикулярним. Його формування може проходити на раннiх етапах утворення бейниту i фактично завершується при подальшому зниженнi температури i придушеннi дифузiйних процесiв. Перлiтне перетворення також не виключалося з розрахунку при розглядi протiкання бейнiтного перетворення. Але фактично воно також припиняється через малу дифузiю при низьких температурах. Швидкiсть утворення мартенситних елементiв покладалася миттєвою. Кiлькiсть мартенситу залежить вiд поточного складу i температури. Розрахунок бейнiтного i дифузiйних (ферритного або перлiтного) перетворень формально не вiдключається при розглядi протiкання мартенситного, але фактично їх швидкостi вже вкрай низькi.

Пiдсумовуючи, можна зазначити, що розроблено пiдхiд до моделювання термодинамiки i кiнетики розпаду переохолодженого аустенiту у легованих багатокомпонентних сталях. Створено вiдповiдну комп'ютерну програму. Пiдхiд базується на фiзично обґрунтованих рiвняннях, що описують фазовi рiвноваги, швидкостi зародження i зростання вiдомих у сталях фаз та структурних складових (ферит, цементит, перлiт, бейнiт, мартенсит), дифузiю елементiв у твердому розчинi. Процес може бути описаний за допомогою методу скiнчених рiзностей. Температура при цьому може прийматися як незмiнною (iзотермiчнi умови) так i такою, що знижується (охолодження). Можливо також задати нелiнiйну змiну температури i навiть термiчнi цикли. Процес змiнення температури у часi може бути додатково описаний шляхом вирiшення теплофiзичної задачi: чисельне вирiшення нестацiонарного рiвняння теплопровiдностi та опис теплообмiну з навколишнiм середовищем (конвекцiя та випромiнювання). Останнє дає змогу використовувати розроблену модель для опису кiнетики фазових перетворень, що мають мiсце у металi реальних виробiв, в тому числi i складної форми, зварних з'єднаннях, металопрокатi. Врахування впливу попередньої деформацiї дає змогу використовувати розроблену модель для опису фазових i структурних перетворень у процесах деформацiйно-термiчної обробки.

РОЗДIЛ 3

Верифiкацiя розробленої моделi розпаду аустенiту

Для верифiкацiї моделi були проведенi експерименти, результати яких зiставлялися з розрахунковими даними. Експеримент полягав у записi дилатометрiчної кривої в процесi охолодження. Зiставлення даної кривої зi змiною температури дає iнформацiю про температури фазових перетворень; її характер (форма) дозволяє судити про iнтенсивнiсть їх протiкання в тому чи iншому iнтервалi. В якостi експериментального матерiалу використана низьковуглецева сталь з пiдвищеним вмiстом Mn i Ni, що мiстить помiтнi кiлькостi Si, Mo, Cu i Cr. Дослiджувана сталь в тiй або iншiй кiлькостi мiстить всi елементи, що враховуються в моделi. Хiмiчний склад сталi i середнiй розмiр зерна аустенiту в нiй наведено в таблицi 1.

Таблиця 3.1 - Склад сталi в верифiкацiйному експериментi (мас.%) i розмiр вихiдного зерна аустенiту в зразках (мкм)

На рисунку 3.1 наведено зiставлення кривих перетворення аустенiту, отриманих з комп'ютерної моделi (а) i в експериментi (б) для двох швидкостей охолодження 10 i 45 град./с.

З зiставлення вiдповiдних кривих на рисунках 3.1 (а) та (б) можна зробити висновок про задовiльну вiдповiднiсть результатiв комп'ютерної моделi експериментальним даним [131]. Температури фактичного початку перетворення передбаченi досить точно. Так, згiдно з експериментальними даними, вони складають 656 ®С (для 10 град./с) i 653 ®С (для 45 град./с), за результатами комп'ютерної моделi вони складають вiдповiдно 675 ® С i 662 ®С. Видно характерне змiщення кривої влiво при збiльшеннi швидкостi охолодження. Також вiдповiдає експерименту той факт, що при швидкостi охолодження 10 град./с до 500 ®С розпадається приблизно 95% аустенiту, пiсля чого перетворення сповiльнюється, а при швидкостi охолодження 45 град./с перетворення фактично завершується при температурi близько 300 ®С.

а) б)

Рисунок 3.1 - Зiставлення експериментальних даних

з результатами комп'ютерної моделi:

а) комп'ютерна модель; б) експеримент

Таким чином, запропонована комп'ютерна модель досить достовiрно прогнозує основнi характернi точки фактичного початку i кiнця перетворення аустенiту, що мають найбiльше практичне значення. Але сам хiд теоретичної i експериментальної кривої трохи рiзниться: так комп'ютерна модель передбачає значно бiльшу швидкiсть процесу на початкових етапах перетворення (пiсля iнкубацiйного перiоду) i його бiльш значне уповiльнення на пiзнiх етапах. На теоретичнiй кривiй для швидкостi охолодження 45 град./с є виражений злам, вiдповiдний початку (зсувного) мартенситного перетворення, на експериментальнiй вiн виражений менш сильно i змiщений в область бiльш високих температур. В цiлому, вiдмiнностi мiж результатами моделювання i експериментом можуть бути частково обумовленi тим, що реальна швидкiсть охолодження була непостiйна, але змiнювалася в ходi процесу. Так, мiг мати мiсце бiльш iнтенсивний тепловiдвiд при високих температурах i його зменшення при зниженнi температури. Швидкiсть охолодження при моделюваннi задавалася постiйною в усьому iнтервалi температур.

Ще краща вiдповiднiсть результатiв моделювання спостерiгається з даними, наведеними в роботi [135]. Хоча слiд зазначити i бiльш простий склад сталi в зазначенiй роботi (0,07% С, 0,76% Mn i 0,1% Si). На рисунку 3.2 наведено зiставлення результатiв розрахунку по комп'ютернiй моделi (а) з аналогiчними кривими (б), побудованими за даними роботи [135] для швидкостей охолодження 8,5 i 50 град./с. Найбiльш iстотною вiдмiннiстю є передбачене моделлю помiтне уповiльнення перетворення пiсля розпаду 90...95% аустенiту, яке було не таким значним в експериментi.

а) б)

Рисунок 3.2 - Зiставлення результатiв комп'ютерної моделi

з лiтературними даними [131]:

а) комп'ютерна модель; б) експеримент

Для пiдвищення адекватностi моделi пiсля зiставлення з експериментом було проведено уточнення деяких важковимiрюваних параметрiв, данi про якi в лiтературi рiзняться. Зокрема шляхом оптимiзацiї отриманi наступнi значення.

- ефективна поверхнева енергiя зародка фериту ?_eff = 0,055 Дж/м²;

- параметр K₁(x), який описує вплив хiмiчного складу на фактичне значення поверхневої енергiї зародка фериту:

K₁(x) = k₀ + 0,15?[Mn,%] + 1.0?[Mo,%] (3.1)

Значення k₀ є поправка на моду процесу i становить приблизно 0,05 для першої моди i 0,5 для другої.

K₂(x) = 1 + 0,9?[Ni,%] (3.2)

- коригувальнi параметри росту зерен фериту:

?_a1 = 2,6; ?_a2 = 4,3; ?_v1 = 800; ?_v2 = 3000;

- параметри зародження бейниту:

k_w1 = 1,2; k_w2 = 0,75; k_L1 = 2,0; k_L2 = 0,5; k_tr1 = 1?10^-10;

- фактор C_i який враховує вплив ступеня дефектностi кристалiчної структури в характерному мiсцi зародження, на рiвень рухливостi атомiв, для першої i другої моди процесу, вiдповiдно:

C₁ = 3,4?10⁶ К^1/2/с?м³; C₂ = 5,7?10⁴ К^1/2/с?м³;

При попереднiх розрахункiв у якостi вiдправних точок бралися значення параметрiв з робiт [6, 11, 53]

На рисунку 3 приведено зiставлення кривих перетворення аустенiту, отриманих за допомогою комп'ютерної моделi з уточненими параметрами (а) i в експериментi (матерiал - сталь складу як у таблицi 3.1) (б) для швидкостей охолодження 10 i 45 град./с [132].

З зiставлення вiдповiдних кривих на рисунку 3 можна зробити висновок про високу достовiрнiсть уточненої моделi i вiдповiднiсть її результатiв експериментальним даним. Температури фактичного початку перетворення передбаченi досить точно.

Було проведено додатковий експеримент з використанням сталi, складу близького до наведеного в таблицi 3.1, але такого, що трохи вiдрiзняється (в межах марки) i розмiром зерна 50 мкм. Склад сталi наведено у таблицi 3.2.

Таблиця 3.2 - Склад сталi у верифiкацiйному експериментi (мас.%) i розмiр вихiдного зерна аустенiту в зразках (мкм)

Результати зiставлення розрахункових кiнетичних кривих з експериментальними точками наведено на рисунках 3.4-3.7.

Рисунок 3.3 - Зiставлення експериментальних даних з результатами

уточненої комп'ютерної моделi

Рисунок 3.4 - Зiставлення експериментальних даних з результатами

уточненої комп'ютерної моделi (5 град. / с)

Рисунок 3.5 - Зiставлення експериментальних даних з результатами

уточненої комп'ютерної моделi (10 град./с)

Рисунок 3.6 - Зiставлення експериментальних даних з результатами

уточненої комп'ютерної моделi (17 град./с)

Рисунок 3.7 - Зiставлення експериментальних даних з результатами

уточненої комп'ютерної моделi (30 град./с)

З наведеного зiставлення видно, що модель адекватна i має гарну передбачувальну здатнiсть. Таким чином, хоча розроблена комп'ютерна модель i не є повною альтернативою експериментальним дослiдженням, але тим не менше вона дозволяє швидко i з мiнiмальними витратами отримати достатнi для практичних цiлей i цiлком достовiрнi данi про кiнетику розпаду аустенiту в заданiй сталi. Наведенi приклади не вичерпують всiх можливостей даної моделi, включаючи розрахунок рiвноважних критичних точок, передбачення моментiв початку фактичного утворення тих чи iнших фаз, прогнозування кiлькiсних характеристик структури металу, впливу попередньої деформацiї i навiть теоретичний розрахунок термокiнетичних i iзотермiчних дiаграм. Отриманi за допомогою розробленої комп'ютерної моделi результати можуть використовуватися при термiчнiй обробцi сталей рiзного складу, а також для опису процесiв, що мають мiсце в зварних швах i зонах термiчного впливу.

РОЗДIЛ 4

Результати моделювання розпаду переохоложденого аустенiту в сталях

4.1 Приклади розрахункiв за розробленою комп'ютерною моделлю фазових перетворень

Для випробування можливостей розробленої програми у роботi [136] було виконано ряд розрахункiв перетворення переохолодженого аустенiту в умовах охолодження для сталей трьох рiзних складiв, наведених в таблицi 4.1. Розмiр вихiдного зерна аустенiту приймався таким, що дорiвнює 40 мкм для всiх випадкiв.

Таблиця 4.1 - Склади сталей, прийнятi при моделюваннi, мас. %

Всi три склади являють собою досить поширенi типи конструкцiйних сталей i приблизно вiдповiдають: склад 1 - сталi 20, склад 2 - сталi 40ХН, склад 3 - сталi 08Г2М. Останнiй склад також може додатково мiстити ванадiй i нiобiй (08Г2МФБ), але в силу малого вмiсту (сотi частки вiдсотка) вплив їх на кiнетику розпаду аустенiту не дуже значний i не враховувався в моделi.

З використанням розробленої моделi для кожного з вищенаведених способiв легування були побудованi квазiбiнарнi полiтермiчнi розрiзи дiлянок дiаграми стану Fe - (C + легуючi елементи) поблизу евтектоїдних перетворень (рисунок 4.1). Також на дiаграмi нанесенi розрахунковi екстраполяцiї її лiнiй в нерiвноважнi областi (позначенi пунктиром). Дiаграми розрахованi в наближеннi парарiвноваги.

а)

б)

в)

Рисунок 4.1 - Розрахунковi дiаграми стану Fe-C для систем легування, вiдповiдних складам в таблицi 12: а) склад 1; б) склад 2; в) склад 3

Термодинамiчний розрахунок фазових рiвноваг був необхiдний в процесi розрахунку кiнетики з наступних причин: визначення принципової можливостi перетворення аустенiту при данiй температурi, визначення рiвноважного складу фаз i кiлькостi кожної з фаз, до якого прагне в ходi перетворення система, також був потрiбний розрахунок змiни енергiї Гiббса при протiканнi перетворення.

Отриманi дiаграми можуть бути використанi при описi перетворення в умовах повiльного охолодження, коли система наближається до рiвноважного стану. Також вони можуть бути застосованi в технологiях термiчної обробки при нагрiваннi, коли треба знати положення рiвноважних точок A₁ i A₃, щоб гарантовано нагрiти до аустенiтної областi або вище перлiтного перетворення (зазвичай на кiлька десяткiв градусiв вище цих характерних температур).

З наведених на рисунку 4.1 дiаграм видно, що легування змiщує положення лiнiй дiаграми Fe-C. Для першого складу змiщення лiнiй у порiвняннi з бiнарною системою Fe-C незначне. У складi 2 змiщення лiнiй є бiльш помiтним. Легування знижує рiвноважнi температури початку феритного перетворення i евтектоїдного (перлiтного) перетворення. При нульовому вмiстi вуглецю температура початку феритного перетворення складає ~ 880 ®С, а перлiтного (А₁) ~ 690 ®С. Помiтно "влiво" змiщується точка евтектоїда i вiдповiдає 0,73% С.

Склад 3 мiстить значну, в порiвняннi з першими двома, кiлькiсть марганцю i має пiдвищену концентрацiю молiбдену. Таке легування мало змiщує положення евтектоїдної горизонталi, але знижує рiвноважнi температури початку феритного перетворення. Зсув "влiво" точки евтектоїда досить малий.

Для кожного з складiв моделювали розпад аустенiту при швидкостях охолодження: 100, 10, 1 i 0,1 ®С/с. На рисунку 3 наведенi вiдповiднi кiнетичнi кривi процесу розпаду аустенiту. Кiлькiснi характеристики отриманих за моделлю результатiв наведенi в таблицi 4.2.

При швидкостi охолодження 100 ®С / с для всiх зазначених вище складiв спостерiгається утворення мартенситу, що вiдбивається характерним зламом на кривiй. Для складу 1 мартенситне перетворення починається при ~ 470 ®С. Стiйкiсть переохолодженого аустенiту в такiй сталi невисока i до цього моменту значна його частина перетворилася у ферит по дифузiйному механiзму. Бейнiт i перлiт в даному випадку практично не утворюється. Завершується мартенситне перетворення при 260 ®С

Легування хромом i нiкелем в складi 2 забезпечує досить високу стiйкiсть переохолодженого аустенiту i знижує температуру початку мартенситного перетворювання. Мартенситне перетворення в данiй сталi починається при 320 ®С. Склад 3 мiстить 2% Mn, але при цьому мало вуглецю. Стiйкiсть переохолодженого аустенiту в ньому вище, нiж в першому складi, температура початку мартенситного перетворення становить ~ 400 ®C.

Швидкiсть охолодження 10 ®С/с для даних складiв характеризується утворенням малої кiлькостi мартенситу i змiщенням початку цього перетворення в область бiльш низьких температур. Температура фактичного початку дифузiйних перетворень при цьому складає для зазначених складiв, вiдповiдно: 790 ®С, 660 ®С i 720 ® С. Частка фериту в складi 1 в кiнцевiй структурi становить 76,7%, утворення ацикулярного фериту не було передбачено, завершується феритне перетворення при 720 ®С. Мартенситне перетворення вiдбувається при температурах нижче 240 ®С.

У складi 2 феритне перетворення завершується при температурi близько 600 ®С, а частка фериту становить 41,3 %, ацикулярний ферит вiдсутнiй. Мартенситне перетворення починається при 250 ®С. До моменту досягнення 150 ®С частка мартенситу становить 32,7% (крайня точка на графiку); при 20 ®С вона становить уже 45,4 %. Кiлькiсть залишкового аустенiту - приблизно 3,6%.

а)

б)

в)

Рисунок 4.2 - Результати моделювання кривих розпаду аустенiту при рiзних швидкостях охолодження (1 - 100 град. / с; 2 - 10 град. / с; 3 - 1 град. / с; 4 - 0,1 град. / с;): а) склад 1; б) склад 2; в) склад 3

Таблиця 4.2 - Характеристика, отриманих при розпадi аустенiту кiнцевих структур (спираючись на результати моделювання)

У складi 3 частка фериту становить приблизно 91,8%, при цьому близько 0,7% приходиться на ацикулярний ферит. Завершується феритне перетворення при 640 ®С. Мартенситне перетворення починається при ~ 210 ®С i практично завершується при кiмнатнiй температурi.

При швидкостi охолодження 1 ®С/с в складах 1 i 3 мартенсит не утворюється, в складi 2 його частка незначна ~ 0,4%. При такiй швидкостi охолодження бiльший, в порiвняннi з попереднiми випадками, вiдсоток припадає на бейнiтнi i перлiтнi структури. Температури фактичного початку феритного перетворення значно змiщуються в область бiльш високих температур i вiдповiдно становлять 820 ®С, 700 ®С i 750 ®С, що ближче до рiвноважних точок A₃. У складi 2 частка фериту помiтно зростає до 49,7%. Завершується феритне перетворення при 660 ®С. Зростає i частка перлiту. Значно збiльшується частка бейнiту. У складi 3 частка фериту змiнюється мало. Феритне перетворення завершується при 710 ®С. Частка перлiту помiтно зростає.

При швидкостi охолодження 0,1 ®С/с передбачається утворення ще ближчих до рiвноважних структур. У складi 2 спостерiгається утворення бейниту, але в значно меншiй кiлькостi, нiж при 1 ®С/с. Температури початку феритного перетворення ще бiльше наближаються до рiвноважних i складають 850 ®С, 710 ®С i 760 ®С. У складi 1 кiлькiсть фериту змiнюється мало i складає 77,1%. Завершується феритне перетворення при 720 ®С. Перлiтне перетворення завершується при ~ 600 ®С. Утворення бейнiту i мартенситу не передбачається. У складi 2 кiлькiсть фериту трохи зменшується i становить 46,8%. Перетворення завершуються при 460 ®С. У складi 3 частка фериту ще трохи зростає i становить 93,8%. Перетворення завершуються при 670 ®С.

Таким чином, розроблена комп'ютерна модель дає результати, якi досить близько узгоджуються з вiдомими закономiрностями. Зниження швидкостi охолодження веде до наближення структур до рiвноважних: зменшується частка, а потiм i зовсiм не спостерiгаються мартенсит, бейнiт i ацикулярний ферит; в перлiтi знижується частка сорбiту та троститу; зростає, а потiм стабiлiзується кiлькiсть фериту i перлiту. Ступiнь залежностi процесiв структуроутворення вiд швидкостi охолодження сильно залежить вiд легування. Так, легування хромом, нiкелем i марганцем сприяє формуванню бiльшої кiлькостi мартенситу при високiй швидкостi охолодження. У той же час при легуваннi марганцем i молiбденом i малому вмiстi вуглецю для усунення утворення мартенситу i бейнiту потрiбне менше зниження швидкостi охолодження, нiж при наявностi хрому i нiкелю.

4.2 Комп'ютерне моделювання розпаду аустенiту в об'ємi

Швидкiсть охолодження реальних виробiв є непостiйною у часi i неоднорiдною в об'ємi. Розроблена комп'ютерна модель дозволяє врахувати цю неоднорiднiсть i дозволяє передбачити неоднорiднiсть структури в рiзних дiлянках виробу. Прикладом такого розрахунку є дослiдження проведене у роботi [132].

Дослiджуваний матерiал являв собою звичайну низьковуглецеву сталь зi складом, наведеним в таблицi 4.3.

Таблиця 4.3 - Склад матерiалу, прийнятий при дослiдженнi (маса%).

Початковий середнiй розмiр зерна аустенiту був встановлений 40 мкм. Розрахунковi значення критичних точок рiвноваги для цiєї сталi: А₁ = 728,7®С, А₃ = 902,1 ®С. Використовуючи модуль термодинамiчних розрахункiв розробленої комп'ютерної моделi, в рамках парарiвноважного пiдходу було розраховано частину квазiбiнарної фазової дiаграми Fe-C. Розрахунки проводились для температурного дiапазону вiд 200 до 1000 ®С i вмiсту вуглецю вiд 0 до 1,5 %. Концентрацiї iнших елементiв вiдповiдають даним таблицi 4.3. Розрахована дiаграма показана на рисунку 4.3. Розрахунковi лiнiї дiаграм, екстрапольованi на нерiвноважну (переохолоджену) дiлянку, показанi пунктиром. Вмiст вуглецю у данiй сталi вiдображається вертикально сiрою лiнiєю.

Як видно з рисунка 4.3, фазова дiаграма Fe-C для цiєї сталi дуже близька до такої дiаграми для бiнарної систем Fe-C.

Рисунок 4.3 - Розрахована частина квазiбiнарного розрiзу фазової дiаграми Fe-C для дослiджуваної сталi

Через рiзну i нелiнiйну швидкiсть охолодження у поперечному перетинi зразка виникають рiзнi умови процесу трансформацiї аустенiту. Внаслiдок цього змiнюється структура вздовж радiуса виробу. На рисунку 4.4 показанi iмiтацiйнi кривi охолодження, що вiдповiдають точкам вздовж радiусу (вiд поверхнi до центру).

Сталi подiбного типу вiдомi як погано змiцнюванi при гартуваннi та як такi, що мають низьку стабiльнiсть переохолодженого аустенiту. Але їх можна гартувати, наприклад пiсля карбюризацiї поверхнi або нiтроцементацiї. Iнший аспект полягає в тому, коли така сталь швидко охолоджується пiд час деякої iншої технiчної обробки. Таким чином, отримання iнформацiї про структуру, утворену не тiльки на поверхнi, але й в глибинi виробу, також є важливою технологiчною задачею.

Рисунок4.4 - Результат моделювання кривих охолодження на рiзних вiдстанях вiд поверхнi зразка.

Для кожної з показаних кривих охолодження було виконано моделювання процесу трансформацiї аустенiту. Це було зроблено для отримання карти структурних типiв у поперечному перерiзi зразку. Отриманi кiнетичнi кривi перетворення аустенiту показанi на рисунку 4.5, а результати моделювання структури показанi на рисунку 4.6.

Рисунок 4.5 - Розрахованi кiнетичнi кривi перетворень аустенiту на рiзних вiдстанях вiд поверхнi зразка

Кiнетичнi кривi, показанi на рисунку 4.5, демонструють процес перетворення аустенiту на трьох рiзних вiдстанях вiд поверхнi: 2 мм, 6 мм та 10 мм (центральна вiсь).

Близько до поверхнi швидкiсть охолодження в першi секунди процесу досить висока. Отже, як видно з форми кривої на вiдстанi 2 мм, мала частина (близько 12%) аустенiту, перетворено на ферит у дiапазонi температур, де можливий такий тип перетворення. При температурi 440 ®С починається мартенситне перетворення, яке триває до близько 370 ®С. Пiдчас феритного перетворення вiдбувається процес обмiну вуглецем мiж аустенiтом i феритом. У цьому процесi поточний вмiст вуглецю в аустенiтi зростає. Процес протiкає (особливо при швидкому охолодженнi) нерiвноважно, а вмiст вуглецю стає не рiвним всерединi зерна аустенiту: вище бiля межi зерна (там, де йде процес утворення фериту) i нижче в серединi (оскiльки дифузiйний процес вiдбувається не миттєво). Згiдно з моделюванням до моменту початку мартенситного перетворення (на вiдстанi 2 мм вiд поверхнi) середня концентрацiя вуглецю в аустенiтi становить близько 0,104%. Це лише трохи бiльше, нiж на початку процесу. Таким чином, отриманий мартенсит буде низьковуглецевим.

Кiнетичнi кривi на вiдстанях 6 i 10 мм мають незначнi вiдмiнностi. Феритовi перетворення в цих областях бiльш повнi. До приходу температури до 500 ®C ~83...85 % аустенiту вже перетворюється на ферит. Тодi процес перетворення стає повiльнiшим. Обмiн вуглецем мiж феритом та аустенiтом у цьому випадку є бiльш значним. Середня концентрацiя вуглецю в аустенiтi при температурi 650 С, у цьому випадку (область бiля центральної осi зразка), становить близько 0,23%. При 520 ®С його вмiст становить 0,53%. Це за термодинамiчним розрахунком є достатнiм (при цiй температурi) для початку формування перлiту. Але насправдi кiлькiсть утворюваного перлiту дуже мала (див. рисунок 4.6 нижче). Також утворюється незначна частка бейнiту. Через збiльшення вмiсту вуглецю в аустенiтi температура початку мартенситного перетворення стає нижчою. Таким чином, на вiдстанi 6 мм вiд поверхнi вона починається при 327 ®С, а в центрi при температурi 308 ®С . Таким чином, незважаючи на значно меншу частину мартенситу, нiж бiля поверхнi зразка в центрi, вiн мiстить бiльше вуглецю, тому може бути дещо твердiшим.

На рисунку 4.6 показанi розрахунковi результати розподiлу типу структури по перерiзу зразка.

а) б)

Рисунок 4.6 - Результати моделювання структуроутворення поперечного перерiзу зразку: а) ферит та мартенсит: б) перлiт та бейнiт

Як i слiд було очiкувати, цей стальний зразок пiсля охолодження у водi буде мати структуру з високим рiвнем мартенситу лише поблизу поверхнi. На вiдстанi 4 мм вiд поверхнi частина мартенситу за результатами моделювання складе лише близько 20%. Отже, у цьому зразку тiльки першi 2 мм вiд поверхнi можна практично повнiстю загартувати. Структура на цiй вiдстанi i далi стає бiльш феритною. Частка мартенситу знижується в напрямку центральної осi, але повiльнiше, нiж на перших 4 мм. Частки перлiту та бейнiту невеликi скрiзь, вони становлять не бiльше 0,5 %. На вiдстанi до 6 мм i далi частка перлiту стає меншою. Частка бейнiту росте вiд поверхнi до центру. Така поведiнка може бути викликана нелiнiйною формою кривих охолодження. Цьому сприяє бiльш повне перетворення фериту при пiдвищенiй температурi, що призводить до збiльшення вмiсту вуглецю в аустенiтi. Це збiльшення вмiсту вуглецю сприяє утворенню перлiту та бейнiту (для цього потрiбен вищий вмiст вуглецю).

Результати моделювання структуроутворення були доведенi реальним експериментом гартування подiбного зразка. Зразок виготовляли з розлитої, а потiм вiдпаленої сталi з аналогiчним складом. Це означає, що в експериментi не було впливу деформацiї на фазовi перетворення. Мiкроструктура зразка вивчалась на дiлянках бiля 2 мм, 6 мм та 10 мм вiд поверхнi. Отриманi фотографiї структур (оптична металографiя) показанi на рисунку 4.7.

a) б) в)

Рисунок 4.7 - Мiкроструктура зразка пiсля гартування (збiльшення в500):

а) 2 мм вiд поверхнi; б) 6 мм вiд поверхнi; в) бiля центральної осi

З показаних фотографiй структури можна побачити, що матерiал на вiдстанi 2 мм вiд поверхнi зразка складається в основному з мартенситу з низьким вмiстом вуглецю, який знаходиться в матрицi фериту. Але вмiст фериту досить невеликий. В районi 6 мм вiд поверхнi структура стає бiльш феритною, але спостерiгається деякий вмiст мартенситу (~ 15%), який знаходиться переважно за межами феритних зерен. Структура в центрi майже однакова на вiдстанi 6 мм вiд поверхнi.

Вимiрюванi значення твердостi в рiзних дiлянках по перетину зразка також вiдповiдають структурним змiнам. Отриманi значення твердостi (за шкалою Роквела):

- на вiдстанi 2 мм вiд поверхнi - 27 Ђ 2 HRC;

- на вiдстанi 6 мм вiд поверхнi - 90 Ђ 3 HRB;

- бiля центральної осi - 89 Ђ 3 HRB

Таким чином, моделювання показує, що гартування такого зразка призводить до поверхневого загартування, яке важливо для обробки цементацiєю або нiтроцементацiєю. I бiльша частина об'єму металу матиме феритову структуру, яка є бiльш пластичною i менш крихкою, але трохи змiцненою певною кiлькiстю мартенситу.

4.3 Моделювання трансформацiї аустенiту для розробки технологiї керованої прокатки

Фазовi перетворення при деформуваннi та охолодженнi вивчали з використанням розробленої моделi. Дослiджений режим контрольованої прокатнки включає наступнi етапи: високотемпературна деформацiя (де вiдбувається перекристалiзацiя аустенiту); швидке охолодження до температур, близьких до рiвноважного феритного перетворення; остаточна деформацiя перед початком фактичного перетворення (iнкубацiйний перiод); швидке охолодження до фактичного перлiтного перетворення; бiльш повiльне охолодження до закiнчення перлiтного перетворення; некероване повiтряне охолодження [137]. Комп'ютерне моделювання було використано для прогнозування рiвноважних та фактичних температур початку та закiнчення перетворення, а також визначення оптимальних показникiв охолодження. На базi термодинамiчного розрахунку передбачено, що значення критичних точок (склад сталi наведено таблицi 4.4) мають наступнi значення: А₃ = 864 ®С, А₁ = 726 ®С. За умов швидкого охолодження, фактична температура початку трансформацiї значно нижче.

Таблиця 4.4 - Хiмiчний склад сталi (мас. %)

Проведено обчислювальний експеримент для визначення оптимального режиму охолоджування для отримання феритно-перлiтної структури (з невеликою кiлькiстю бейнiту) з малими розмiрами феритних зерен. Чисельнi параметри запропонованого режиму виглядають наступним чином. Висока деформацiя в iнтервалi температур 1200 - 1130 ®С, при її ступенi не менше 50%. При температурах вище 1200 ®С карбiдоутворюючi елементи (V, Nb, Ti) в основному розчиненi в аустенiтi (термодинамiчний розрахунок). У зазначеному вище iнтервалi карбiди Nb та Ti частково видiляються, що перешкоджає росту зерна. Перекристалiзацiя аустенiту, що вiдбувається, призводить до формування не довгастих, а кулястих i дрiбних зерен аустенiту. Потiм метал охолоджується зi швидкiстю 5...8 ®С/с до температури 830 ®С. Тодi залишкова деформацiя виконується зi ступенем 40...70 %. Кiнцева температура фiнальної деформацiї становить 760 ®С. Потiм метал охолоджувався до 650 ®С зi швидкiстю 4...7 ®С/с. Пiсля цього швидкiсть охолодження сповiльнюється до 0,1...0,3 ®С/с до досягнення металом температури 520 ®С. У цей перiод формуються перлiт i дисперснi спецiальнi карбiди. Цим фазовi перетворення завершуються, тому в наступному перiодi охолодження можна не контролювати i проводити на вiльному повiтрi.

Розрахована кiнетична крива перетворення аустенiту в ходi описаного вище режиму охолодження показана нижче на рисунку 4.8. На ньому також показана крива для подiбного режиму, але без деформацiї. Деформацiя робить процес перетворення фериту бiльш швидким, особливо наприкiнцi перiоду. Це призводить до утворення бiльш тонких феритових зерен через бiльш активне їх зародження (включаючи зародження всерединi зерна).

Рисунок 4.8 - Розрахованi кiнетичнi кривi перетворення аустенiту пiд час дослiджуваного режиму охолодження

Фактична температура початку феритного перетворення становить близько 760 ®С. При цiй температурi кiнцева деформацiя закiнчується. Температура фактичного початку перлiтного перетворення становить близько 650 ®С. Вище вказаної температури, швидкiсть охолодження повинна бути достатньо швидкою, щоб запобiгти утворенню карбiдiв, але досить повiльною для завершення феритного перетворення. Потiм уповiльнення охолодження до 0,1...0,3 ®С/с достатньо для завершення утворення перлiту та карбiдiв вище 520 ®С для запобiгання утворенню бейнiту, що є досить крихкою та нерiвноважною фазою.

Механiчнi властивостi зразкiв сталi, отриманi за запропонованим режимом, наведенi в таблицi 4.5 нижче.

Таким чином, запропонований спосiб дозволяє отримати сталь класу X70 (наближається до X80), значно покращуючи як мiцнiсть, так i пластичнi властивостi та ударну в'язкiсть при нормальних i зниженихемпературах.

Таблиця 4.6 - Механiчнi властивостi сталевих зразкiв пiсля контрольованої прокатки

4.4 Математичне моделювання структуроутворення в областi термiчного впливу зварювального шва низьковуглецевої середньолегованої сталi

Дослiджуваний матерiал представляв собою низьковуглецеву сталь, леговану Ni i Mn, що також мiстить значнi кiлькостi Cr, Cu i Mo, мiкролеговану V, Nb i Ti (сильнi карбiдоутворюючi елементи) [138]. Склад сталi, прийнятий при моделюваннi наведено в таблицi 4.7. Початковий середнiй розмiр зерен аустенiту був покладений рiвним 40 мкм.

Таблиця 4.7 - Хiмiчний склад сталi (мас.%)

Наведений склад вiдповiдає реальним зразкам, використаним при верифiкацiї результатiв моделi. Вплив домiшок S i P явно не враховувалося в розрахунках по моделi, так як їх вмiст малий i вплив на фазовi перетворення та видiлення карбiдiв незначний. Наявнiсть V, Nb, Ti i N враховувалося тiльки при розрахунках утворення карбiдних i карбонiтридних фаз. Сталi подiбного типу характеризуються формуванням деякої кiлькостi бейнiтних i мартенситних структур, здатних утворитися навiть при вiдносно повiльному охолодженнi. Цi фази твердi, але крихкi. Тому їх виникнення звичайно небажано в зварних конструкцiях.

Теплофiзичне моделювання формування зони термiчного впливу виконувалося методом кiнцевих елементiв. Отриманi для звичайного охолодження на спокiйному повiтрi кривi охолодження для рiзних вiдстаней вiд осi зварного шва, показанi на рисунку 4.9. Кривi наведенi з моменту початку перiоду охолодження, який приймався за нуль для кожного випадку.

Рисунок 4.9 - Результати моделювання кривих охолодження на рiзних вiдстанях вiд зварного шва

З наведених графiкiв видно, що метал на рiзних вiдстанях нагрiвався до рiзних температур i час його перебування в певних температурних дiапазонах також вiдрiзняється. Це може призводити до змiни в структурах, якi формуються в рiзних дiлянках.

Термодинамiчнi розрахунки, проведенi за допомогою моделi, показали, що рiвноважнi критичнi точки для даної сталi становлять: A₃ = 778 ®C i A₁ = 659 ®C. Таке зниження цих температур в порiвняннi з дiаграмою стану Fe-C обумовлено наявнiстю легування Ni i Mn. Рiвноважний вмiст вуглецю в перлiтi в точцi А₁, згiдно з розрахунками для наведеного матерiалу, становить 0,68% i знижується при протiканнi перетворення при бiльш низьких температурах.

Для кожної кривої охолодження виконувалося моделювання розпаду аустенiту. Отриманi при цьому кiнетичнi кривi процесу перетворення наведенi на рисунку 4.10. Цi кривi розрiзняються не дуже iстотно, але вони не однаковi. З них видно, що фактичне перетворення в данiй сталi починається пiсля значного iнкубацiйного перiоду i за умов переохолодження нижче рiвноважної температури.

Активне утворення фериту починається приблизно при 660...680 ®C (тобто при переохолодженнi близько 100 ®C). Аналiз результатiв розрахунку показав, що передвидiлення зародкiв фериту в аустенiт починається вже при 720 - 740 ®C, але помiтне збiльшення його частки в структурi починається, коли вони входять в стадiю активного зростання. Далi феритне перетворення протiкає досить швидко i завершується при 580...630 ®C (в залежностi вiд режиму охолодження в данiй дiлянцi). Моделювання показало, що в вiддалених вiд зварного шва дiлянках умови охолодження складаються так, що феритне перетворення завершується при бiльш високих температурах.

Рисунок 4.10 - Результати моделювання кiнетичних кривих розпаду аустенiту на рiзних вiдстанях вiд зварного шва

До настання цього моменту частка аустенiту, який перетворився на ферит, становить близько 91...92%. Структура металу буде переважно феритною, що є нормальним для сталей подiбного типу. Перлiтне перетворення в цiй сталi вiдбувається помiтно повiльнiше, що виражається в характерному вигинi кiнетичної кривої (рисунок 4.10). Нижче 400...450 ®C починається активне бейнiтне перетворення. Велика частина його представляє собою верхнiй бейнiт, що утворюється вище 370 ®C (вiн становить 70 - 80 % вiд усього утвореного бейнiту). Нижче йде утворення нижнього мартенситоподiбного бейнiту. Урахування можливостi мартенситного перетворення було включене у модель, але утворення мартенситних структур не було передбачено для даних умов. Прогнозованi шляхом моделювання характеристики структури для рiзних вiдстаней вiд осi зварного шва наведенi в таблицi 4.8. З даних таблицi видно, що фазовий склад розглянутих дiлянок не вiдрiзняється кардинально, але помiтне деяке зниження частки бейнiту в мiру вiддалення вiд шва при збiльшеннi процентного вмiсту фериту i перлiту в структурi. Це пов'язано з бiльш тривалим перебуванням даних дiлянок металу при температурах протiкання феритного перетворення i початком утворення перлiту при бiльш високих температурах.

Металографiчне дослiдження показало, що частка бейнiтних елементiв в структурi металу iз зони термiчного впливу становить 4 - 7 %, що близько до передбачених за допомогою комп'ютерної моделi даних.

Наявнiсть навiть цiєї невеликої кiлькостi бейнiту може привести до зниження пластичних властивостей. Його присутнiсть в зонi теплового впливу i в зварних швах з такого типу сталей є вiдомим фактом, але вона небажана.

Деякi автори рекомендують для запобiгання утворенню бейнита в подiбних сталях повiльне охолодження пiсля зварювання [139, 140]. Це має сенс, але моделювання показує, що навiть швидкiсть охолодження близько 2 ®С/с призводить до утворення деякої кiлькостi бейнiту. Крiм того, як видно з рисунка 4.9, швидкостi вiльного охолодження непостiйнi в часi i не в повнiй мiрi контролюються. Також реальна швидкiсть охолодження сильно залежить вiд розмiру i геометрiї виробу. Таким чином, найкращим способом для бiльш значущого запобiгання утворенню бейниту є охолодження iз заданою непостiйною швидкiстю або термообробка з контрольованим охолодженням виробу пiсля зварювання.

Таблиця 4.8 - Прогнозованi на пiдставi моделювання характеристики

структури на рiзних вiдстанях вiд середини зварного шва

Нами була проведена серiя обчислювальних експериментiв (моделювання) з метою розробки режиму контрольованого охолодження, який мiг би зробити структуру сталi бiльш ферито-перлiтною i менш бейнiтною без небезпеки значного зростання зерна. Також були врахованi температурнi iнтервали, в яких карбiди ванадiю i нiобiю могли видiлятися з аустенiту. Розрахованi температури становлять для NbC - 1020...740 ®C i для VC - 790...550 ®C. При цих температурах утворюється велика частина карбiдiв цих елементiв в умовах повiльного охолодження. Данi карбiди здатнi утворювати дисперсну фазу, яка пiдвищує мiцнiснi властивостi без зниження пластичностi, але тiльки тодi, коли їх розмiри малi i утворення їх вiдбувається всерединi зерна i вони когерентно пов'язанi з матрицею, а не знаходяться в межах зерен. Чим менше температура їх формування, тим бiльше дисперсними (а, отже, i ефективними) вони будуть. Таким чином, бiльш швидке охолодження в початковий перiод i уповiльнення його в перiод, коли температура досить низька, дозволить полiпшити умови формування дрiбнодисперсних змiцнюючих фаз.

На рисунку 4.11 наведено режим контрольованого охолодження такої сталi пiсля зварювання, що дозволяє, як показують результати комп'ютерної моделi, практично уникнути утворення бейнiтних складових i забезпечити сприятливi умови для утворення спецiальних дисперсних карбiдiв.

Рисунок 4.11 - Режим керованого охолодження, запропонований на основi результатiв моделювання

Початкова температура встановлена такою, що дорiвнює 880 ®C. Її можна розглядати як температуру нагрiвання при термообробцi пiсля зварювання. Якщо вирiб охолоджується безпосередньо пiсля зварювання без можливостi термообробки, швидкiсть охолодження вище цiєї температури повинна бути такою, як показано на графiку для першої хвилини. На початку обробки швидкiсть охолодження вiдносно велика: 3,8...4,6 ®С/с. Ця швидкiсть охолодження повинна зберiгатися до того, як температура металу стане 640 ®С. У цей перiод немає потреби в уповiльненому охолодженнi, тому що ферит утворюється i зростає досить швидко, крiм того, тривалий час витримки при температурах вище 800...850 ®С може призводити до зростання зерен, а також до випадання великих карбiдiв в межах зерен, що небажано. Потiм швидкiсть охолодження повинна бути значно зменшена до 0,08...0,12 ®С/с. Така швидкiсть охолодження повинна зберiгатися до тих пiр, поки температура металу не стане 490...500 ®C. Цей перiод займе близько 22...25 хвилин. Цього достатньо для формування дисперсного перлiту без бейнiту. Цей перiод також корисний для утворення дисперсної карбiдної фази. Швидкiсть охолодження у наступний перiод не дуже важлива i може становити 1...3 ®С/с, що характерно для звичайного охолодження на повiтрi.

Моделювання показує, що описаний вище режим охолодження призводить до формування структури, яка мiстить близько 91% фериту i майже 9 % перлiту. Кiлькiсть бейнiту, якщо вiн i утворюється, буде становити менше 0,2 %, що не є критичним.

4.5 Математичне моделювання кiнетики розпаду аустенiту при охолодженнi низьковуглецевої сталi з врахуванням впливу деформацiї

Завданням, що стояло у роботi [141], було створення комп'ютерної моделi, здатної описати кiнетику всього комплексу процесiв, що вiдбуваються при розпадi переохолодженого аустенiту. Розроблена модель [142] дозволяє розрахувати в єдиному процесi феритне, перлiтне, бейнiтне i мартенситне перетворення, а також передбачити кiлькiснi характеристики кiнцевої структури металу. Модель враховує вплив на термодинамiку i кiнетику фазових перетворень таких факторiв як хiмiчний склад (до 6 одночасно присутнiх компонентiв), розмiр початкового зерна аустенiту, ступiнь i температуру попередньої деформацiї металу в аустенитной областi.

Одним з важливих чинникiв при розробцi режимiв деформацiйно-термiчної обробки сталi є вплив деформацiї на кiнетику розпаду аустенiту. У той же час, цi данi (особливо кiлькiснi i для даного конкретного складу) можуть бути мало представленими в доступнiй лiтературi. Проведення експериментальних дослiджень подiбного роду є тривалим, трудомiстким i дорогим процесом. Комп'ютерне моделювання, хоча i не є повною альтернативою натурному експерименту, дає можливiсть швидко i з мiнiмальними витратами отримати необхiднi данi для заданої сталi.

Факт наявностi впливу деформацiї на кiнетику фазових перетворень вiдомий [143, 144]. У той же час, якiснi та кiлькiснi характеристики такого впливу не настiльки однозначнi. Так, наприклад, вiдомо, що деформацiя може сприяти мартенситному i бейнiтного перетворенням [68, 144]. Подiбне твердження буде справедливо, якщо деформацiя вiдбувається при температурах, нижче можливого початку таких перетворень або якщо сталь не схильна або мало схильна до розвитку в нiй процесу розпаду аустенiту. Наявнiсть високотемпературної деформацiї в низьколегованiй сталi прискорює процес феритного перетворення, що обумовлено розвитком дефектностi структури аустенiту i формуванням субзерен. Таким чином, наявнiсть високотемпературної деформацiї аустенiту, може привести до формування бiльшої кiлькостi продуктiв дифузiйних перетворень, i знизити частку продуктiв зсувних перетворень.

Дослiдження кiнетики розпаду аустенiту за допомогою комп'ютерної моделi проводилися на прикладi сталi 15, склад якої наведено в таблицi 4.9.

Розмiр вихiдного зерна аустенiту задавався 60 мкм. Розглянуто ступенi деформацiї 0 i 50%. Температура деформацiї приймалася 930 ®С, тобто дещо вище точки А₃, яка, згiдно з термодинамiчних розрахунками становить для даного складу 894 ®С. Точка А₁ згiдно з цими розрахунками дорiвнює 727 ®С.

Таблиця 4.9 - Склад сталi прийнятий в

розрахунках по моделi, мас. %

Термодинамiчне i кiнетичне моделювання проводилося з використанням розробленої нами спецiальної комп'ютерної програми [142].

На рисунку 4.12 наведенi розрахунковi кiнетичнi кривi розпаду аустенiту у сталi даного складу (таблиця 4.9) для швидкостi охолодження 100 ®С/с. Така швидкiсть охолодження характерна для процесiв гарту i при нiй навiть в сталi подiбного складу можливе утворення деякої кiлькостi мартенситу.

З графiкiв (рис. 4.12) видно, що вплив попередньої деформацiї на кiнетику розпаду аустенiту є суттєвим. Деформацiя практично не змiщує температуру фактичного початку феритного перетворення, але iстотно прискорює його. Так, в обох випадках ??? перетворення стартує приблизно при 785 ®С. Без деформацiї частка фериту в кiнцевiй структурi становить приблизно 42,5%. При цьому глобулярний ферит, що утворюється при температурах вище 645 ®С становить близько 17 %. Решта - це ферит, що зароджується нижче температури, при якiй можливе протiкання бейнiтного перетворення, вiн матиме ацикулярну (голчасту) структуру [28].

Рисунок 4.12 - Результати комп'ютерного моделювання впливу попередньої деформацiї на кiнетику розпаду аустенiту у сталi 15

(швидкiсть охолодження 100 ®С/с)

При температурах нижче 400 ®С вiдбувається мартенситне перетворення, яке повнiстю завершується при 280 ®С. Прискорення феритного перетворення в попередньо деформованому аустенiтi призводить до того, що велика частина аустенiту встигає перетворитися на ферит вже при досягненнi 720 ®С. Пiсля цього починається перлiтне перетворення, яке, однак, вiдбувається не так швидко i перлiту в кiнцевiй структурi дуже мало (всього ~ 0,3%). Частка глобулярного фериту в цьому випадку становить майже 84%. Температура початку мартенситного перетворення сильно змiщується вниз через збагачення вуглецем аустенiту при протiканнi феритного перетворення. Температура його початку складає 230 ®С, а завершиться воно при 190 ®С.

Рисунок 4.13 - Результати комп'ютерного моделювання впливу попередньої деформацiї на змiну середнього розмiру зерна фериту в ходi розпаду аустенiту у сталi 15 (швидкiсть охолодження 100 ® С/с)

На рисунку 4.13 наведенi результати моделювання змiни середнiх розмiрiв зерна фериту в ходi перетворення. На наведених графiках вiдсiчена область iнкубацiйного перiоду, коли фериту ще мало. У цей перiод не виключається формування i зростання деякої кiлькостi зерен фериту, але ймовiрнiсть їх появи, а, отже, i кiлькiсть, вкрай малi.

З наведених результатiв (рис. 4.13) видно, що зародження фериту в попередньо деформованiй сталi йде набагато швидше i, вiдповiдно, кiнцева структура виявляється значно бiльш дрiбнозернистою, а розмiр зерна практично стабiлiзується до моменту закiнчення перетворення. У недеформованому зразку зародження йде повiльнiше, феритне перетворення не встигає завершиться до початку мартенситного. Зерна фериту продовжують рости за рахунок перетворення. Для коагуляцiйного зростання часу недостатньо в обох випадках.

Таким чином, попередня деформацiя не тiльки перешкоджає гартуванню низьковуглецевої низьколегованої сталi при прискореному охолодженнi, а й сприяє формуванню бiльш дисперсної структури фериту.

На рисунку 4.14 показанi результати впливу аналогiчної попередньої деформацiї для тiєї ж сталi, але при швидкостi охолодження 10 ®С/с, з яких видно, що при меншiй швидкостi охолодження вплив деформацiї є менш вираженим.

Рисунок 4.14 - Результати комп'ютерного моделювання впливу попередньої деформацiї на кiнетику розпаду аустенiту в сталi 15

(швидкiсть охолодження 10 ® С/с)

Проте можна вiдзначити збереження тенденцiї прискорення феритного перетворення i перешкоджання утворенню мартенситу. Також передбачено i значне подрiбнення феритного зерна при попереднiй деформацiї вiд бiльш 90 мкм в недеформованiї сталi до 60 мкм в попередньо деформованiй.

Як в недеформованому, так i попередньо деформованому металi феритне перетворення завершується при близьких значеннях температури, приблизно при 715 ®С. Крива (рис. 4.14), вiдповiдна попередньо деформованiй сталi бiльш крута, тобто на початкових i середнiх стадiях перетворення йде швидше. Кiлькiсть перлiту в кiнцевiй структурi при наявностi деформацiї зростає вiд 2,2 до недеформованому до 4,0% в деформованому, але залишається невеликим. Кiлькiсть бейниту, навпаки, знижується вiд 4,2 до 2,1%. У недеформованому зразку передбачалося утворення близько 7% мартенситу; в деформованому станi його утворення не передбачалося.

Таким чином, за допомогою розробленої комп'ютерної моделi [142] змодельовано процес кiнетики розпаду аустенiту в сталях довiльного складу, що дозволяє якiсно i кiлькiсно передбачити формування структури металу. На прикладi низьковуглецевої сталi продемонстрованi можливостi моделi описати вплив попередньої деформацiї на структуроутворення сталi в ходi фазових перетворень. Показано збiльшення швидкостi феритного перетворення в деформованої сталi, що призводять до подрiбнення зерна фериту i запобiгання утворенню низьковуглецевого мартенситу в кiнцевiй структурi.

З використанням комп'ютерної моделi встановленi якiснi та кiлькiснi характеристики впливу попередньої деформацiї аустенiту при 930 ®С в сталi 15. Показано, що попередня деформацiя зi ступенем 50% дозволяє у 1,5 - 2,0 рази (в залежностi вiд iнтенсивностi охолодження) подрiбнити розмiр зерна фериту i запобiгти утворенню низьковуглецевого мартенситу. Ступiнь вираженостi впливу попередньої деформацiї на кiнетику розпаду аустенiту зменшується при зниженнi швидкостi охолодження.

Таким чином, розроблено математичну модель, що дозволяє описати термодинамiку i кiнетику розпаду переохолодженого аустенiту в сталi. Модель дозволяє побудувати дiлянки квазiбiнарних розрiзiв дiаграми Fe - (вуглець + легуючi елементи) i кiнетичнi кривi перетворення, а також якiсно i кiлькiсно прогнозувати тип кiнцевої структури.

Проведено зiставлення результатiв комп'ютерного моделювання з експериментальними даними з кiнетики розпаду аустенiту в комплексно легованiй сталi при рiзних швидкостях охолодження. Результати експерименту пiдтвердили достовiрнiсть i адекватнiсть розробленої комп'ютерної моделi.

Проведено серiю розрахункiв для трьох типових складiв конструкцiйних сталей з метою демонстрацiї можливостей розробленої моделi; встановлена її придатнiсть для опису термодинамiки i кiнетики фазових перетворень.

Можливiсть практичного застосування розробленої моделi була продемонстрована моделюванням загартовування зразкiв низьковуглецевої сталi. Моделювання проводилося з метою передбачення розподiлу мартенситу в поперечному перерiзi, таким чином можна оцiнити глибину прогартованостi. Симуляцiя показала, що повною мiрою загартована глибина в цилiндричному зразку звичайної низьковуглецевої сталi дiаметром 20 мм становить приблизно 2 - 3 мм (в умовах охолодження у водi). Далi по перетину частка мартенситу iстотно знижується, а структура стає переважно з феритною.

Моделювання дозволило вивчити процес перетворення аустенiту на рiзних вiдстанях вiд поверхнi зразка. Таким чином, були визначенi дiапазони температур процесiв формування фериту та мартенситу в рiзних частинах дiлянки перетину зразка. Також було вивчено процес обмiну вуглецю мiж аустенiтом i феритом, що утворюється i був прогнозований середнiй вмiст вуглецю в аустенiтi на момент початку мартенситного перетворення.

Проведено моделювання, яке враховувало вплив деформацiї аустенiту на кiнетику зародження фериту. Показано, що цей вплив досить значний, i попередня деформацiя призводить до бiльш тонкої феритної структури. Розрахунковий експеримент дозволив визначити та оптимiзувати значення дiапазонiв температур та швидкостi охолодження у технологiї керованої прокатки. Запропонована методика призводить до отримання тонкої феритної структури та досить високих мiцнiсних i пластичних властивостей вуглецевої сталi, мiкролегованої сильними карбiдоутворюючими елементами (Ti, Nb, V).

Проведено комп'ютерне моделювання фазових перетворень в зонi термiчного впливу зварювального шва низьковуглецевої сталi, легованої Ni та Mn. Моделювання передбачило формування деякої кiлькостi бейнiтних структур у зонi термiчного впливу, що утворюються при звичайному повiтряному охолодженнi i приводять до зниження пластичних властивостей. Доля цього бейнiту в структурi металу шва та зони термiчного впливу складає близько 4,8 - 6,8 %. Визначено температурнi iнтервали фактичного феритного i перлiтового перетворень при повiтряному охолодженнi з урахуванням неоднорiдностi та нелiнiйної швидкостi охолодження.

Запропоновано режим контрольованого охолодження, що дозволяє уникнути утворення бейнiту у низьковуглецевих сталях, легованих Ni i Mn з пiдвищеним вмiстом Cr, Mo i Cu i мiкролегованих V i Nb, що включає в себе швидке охолодження (близько 3,8 - 4,6 ®С/с ) при температурах вище 640 ®С i значне його зниження (до 0,08 - 0,12 ®С/с) в iнтервалi (640 - 500 ®С), а потiм вiльне охолодження на повiтрi. Такий режим не тiльки дозволяє практично уникнути утворення бейнiту, але i полiпшує умови формування дисперсних карбiдiв V i Nb в мiкролегованих сталях, що знижує вiрогiднiсть крихкого руйнування поблизу зварювального шва.

РОЗДIЛ 5

Дослiдження утворення карбонiтридних фаз у комплексно мiкролегованих i модифiкованих сталях

5.1 Термодинамiчний опис процесiв видiлення карбонитридiв в модифiкованої мiкролегованiй сталi

Фiзико-математичний опис процесiв утворення карбонитридiв у сталях виконано для металу, що охолоджкється i для iзотермiчних умов. В основi моделi лежить метод розрахунку, що базується на фiзико-хiмiчних принципах. Його викладено у роботi [145]. Реакцiї видiлення карбiдiв i нiтридiв з металу можна записати в такий спосiб:

a[X]+b[N]=X_aN_b (5.1)

a[X]+b[C]=X_aC_b (5.2)

Карбонiтрид представляємо як взаємний розчин вiдповiдного карбiду i нiтриду. В цьому випадку можна записати:

(5.3)

(5.4)

(5.5)

де K₁ - константа рiвноваги реакцiї (5.1);

x_XN - частка нiтриду в карбонитридi;

[X] - рiвноважна з карбонiтридом концентрацiя карбiдоутворюючого елементу;

f_X - коефiцiєнт активностi карбiдоутворюючого елемента;

[N] - рiвноважна з карбонiтридом концентрацiя азоту;

x_XС - частка карбiду в карбонiтридi;

f_N - коефiцiєнт активностi азоту;

K₂ - константа рiвноваги реакцiї (5.2);

[С] - рiвноважна з карбонiтридом концентрацiя вуглецю;

f_С - коефiцiєнт активностi вуглецю.

Вирiшення системи рiвнянь (5.3 - 5.5) дозволяє визначити рiвноважний з металом склад карбонитридiв i температуру їх утворення (температура входить в рiвняння неявно, у виглядi залежних вiд неї параметрiв). Константи рiвноваги K₁ i K₂ задаються як функцiї вiд температури (5.6):

(5.6)

де A, B - емпiричнi постiйнi; T -температура, ЊК.

Значення коефiцiєнтiв активностi знаходимо за методом Вагнера, використовуючи параметри взаємодiї першого i другого порядку i данi про хiмiчний склад сталi. Логарифмуючи рiвняння (5.3) i (5.4) i пiдставляючи в них вирази температурних залежностей логарифмiв констант рiвноваги K₁ i K₂, вiдповiдно до виразу (5.6), система основних рiвнянь задачi набуде вигляду:

(5.7)

(5.8)

(5.8)

де A₁, B₁, A₂, B₂ - постiйнi з виразу температурної залежностi константи рiвноваги для реакцiї (5.1) i реакцiї (5.2) вiдповiдно.

Ведемо позначення:

(5.9)

(5.10)

Пiсля пiдстановки виразу (5.9) в рiвняння (5.7) i виразу (5.10) в рiвняння (5.8) система основних рiвнянь задачi набуде вигляду:

(5.11)

(5.12)

(5.13)

Виключимо з отриманої системи T, пiсля перетворення отримаємо:

(5.14)

(5.15)

Рiвняння (5.15) є трансцендентним - не має алгебраїчного вирiшення щодо x_XC в загальному виглядi, але може бути вирiшено чисельно методом iтерацiй. Визначивши значення x_XC з рiвняння (5.15), значення x_XN знаходиться з рiвняння (5.13). Потiм знаходимо приблизне значення температури утворення карбонiтриду:

(5.16)

Потiм уточнюємо значення коефiцiєнтiв активностi. Глобальнi iтерацiї повторюємо до отримання заданої точностi.

У мiру видiлення карбонiтридов з розчину виходять карбонiтрiдоутворюючi елементи, азот i вуглець. Отже, склад твердого розчину змiнюється, що призводить до змiни умов утворення карбонiтридiв. Спираючись на описаний метод розрахунку, нами була створена скiнченорiзницева модель утворення карбонiтридiв при охолодженнi металу. Обчислення виконуються на кожному кроцi розрахунку для всiх наявних в сталi сильних карбонiтрiдоутворюючих елементiв. Сполучено здiйснюється балансовий розрахунок змiни складу твердого розчину. На кожному наступному кроцi розрахунку умови видiлення карбонiтридiв вiдрiзняються, зокрема змiнюються коефiцiєнти активностi елементiв. Застосування зазначеного методу розрахунку дозволило врахувати вплив видiлення бiльш високотемпературних карбонiтридiв на рiвноважнi температурнi iнтервали утворення i склади бiльш низькотемпературних.

Для опису карбонiтрiдоутворення в iзотермiчних умовах застосовано в своїй основi близький, але дещо iнший пiдхiд [146, 147]. Константа рiвноваги реакцiї утворення карбiду або нiтриду з компонентiв розчину дорiвнює:

(5.17)

де K_р - константа рiвноваги;

- активнiсть даної сполуки в карбонiтриднiй фазi;

- активнiсть карбонiтрiдоутворюючго елементу;

- активнiсть вуглецю або азоту;

n, m - стехiометричнi коефiцiєнти рiвняння реакцiї.

Для карбiдiв i нiтридiв вищевказаних елементiв числа n i m можна вважати рiвними 1, а загальну формулу записати як MeR. З визначення активностi i виразу (5.17)
дорiвнює

(5.18)

де
- частка даного карбiду або нiтриду;

,
- вiдповiдно, коефiцiєнти активностi карбонiтрiдоутворювачiв;

- коефiцiєнт активностi сполуки, що утворюється;

,
- вiдповiдно, рiвноважнi з утвореними сполуками масовi концентрацiї карбонiтрiдоутворюючого елементу i вуглецю або азоту.

Масова концентрацiя елемента, рiвноважна з карбонiтридом, дорiвнює вiдношенню рiзницi початкової i витраченої на утворення сполуки його маси, вiднесеної до маси розчину, зменшеної на масу карбонiтридiв, що утворилися. Отже, вираз (5.18) набуде вигляду:

(5.19)

де
,
- вiдповiдно початковi маси карбiдо- або нiтрiдоутворюючого елемента i вуглецю або азоту, що мiстяться в обсязi твердого розчину масою
, кг;

,
- вiдповiдно маси карбiдо- або нiтрiдооутворюючого елемента i вуглецю або азоту витраченi на утворення сполуки, кг;

,
- вiдповiдно маси утворених карбiдiв i нiтридiв, кг;

коефiцiєнт 10000 - необхiдний для тих випадкiв, коли коефiцiєнти активностi розрахованi для процентних концентрацiй.

Маса карбонiтрiдоутворюючого елементу, що пiшов з розчину, дорiвнює:

(5.20)

де
и
- молекулярнi маси елемента i продукту реакцiї.

Маса, витраченого на утворення сполуки, вуглецю або азоту дорiвнює:

(5.21)

Отже:

(5.22)

(5.23)

Вхiднi в рiвняння маси карбiдiв i нiтридiв вважаємо рiвними кiлькостi витрачених на їх утворення елементiв, отже:

(5.24)

(5.25)

=
+
(5.26)

де
,
- витраченi маси кожного з карбонiтрiдоутворюючих елементiв, кг;

,
- витраченi маси вуглецю i азоту вiдповiдно.

Записавши рiвняння (5.22) для кожного з карбiдiв i нiтридiв, видiлення яких передбачається в даному випадку, в сукупностi з рiвняннями (5.24 - 5.26) отримуємо замкнуту систему, рiшення якої дозволяє розрахувати розподiл розглянутих елементiв мiж карбiдами, нiтридами i твердим розчином.

Розрахунок коефiцiєнтiв активностi карбонiтридних фаз проводиться за методом А. Г. Пономаренко (метод оцiнки термодинамiчних функцiй систем з колективiзованими електронами).

5.2 Термодинамiчне дослiдження видiлення карбонiтридних фаз в комплексно мiкролегованiй сталi в процесi охолодження

З використанням методики термодинамiчного моделювання проведена оцiнка температурних iнтервалiв видiлення i складу карбонiтридiв, що утворюються в комплексно мiкролегованих сталях [145]. Нижче наведено приклад розрахунку утворення карбонiтридiв при охолодженнi сталi 08Г2МФБ наступного хiмiчного складу: С - 0,07%, Mn - 1,47%, Si - 0,20%, Ti - 0,013%, Nb - 0,064%, V - 0,065%, Mo - 0,19%, N - 0,006%, Zr - 0,001%. Розрахунок виконаний для випадку повiльного охолодження сталi в рамках припущення, що процес йде рiвноважно.

Карбонiтрид Nb починає видiлятися при 1386 ЊС. Склад перших включень NbC_0,38N_0,61 При зниженнi температури, в мiру видiлення, в ньому росте частка вуглецю (рисунок 5.1 а). На графiку спостерiгається злам при 1223 ЊС, наявнiсть якого пов'язана з видiленням Ti(C, N). При охолодженнi вiд 1124 до 976 ЊС вмiст Nb в твердому розчинi практично не змiнюється (рисунок 5.1 б), що говорить про припинення видiлення карбонiтридiв. У перiод охолодження вiд 976 до 850 ЊС видiляється NbC.

а)

а)

Рисунок 5.1 - Змiна частки карбiдної складової в карбонiтридi Nb, що видiляється (а) i вмiсту Nb в твердому розчинi (б) в мiру зниження температури

а)

б)

в)

Рисунок 5.2 - Маси карбiдiв i карбонiтридiв в 1 кг металу, що видiлилися в рiзних температурних iнтервалах: а) нiобiю; б) титану;

в) цирконiю

На рисунку 5.2 (а) представлена дiаграма, що показує маси карбiдiв i карбонiтридiв нiобiю, що припадають на 1 кг металу, що видiлилися в рiзних температурних iнтервалах. З зiставлення графiка рисунка 5.1 (а) i дiаграми рисунка 5.2 (а) видно, що 53% карбонiтридiв нiобiю мають склад вiд NbC_0,38N_0,61 до NbC_0,47N_0,52; 29 % - вiд NbC_0,47N_0,52 до NbC_0,67N_0,32; 13,5 % - вiд NbC_0,67N_0,32 до NbC_0,99N_0,01; i 4,5 % - карбiд нiобiю.

Утворення Ti (C, N) починається нижче 1220 ®C. Його початковий склад TiC_0,0013N_0,9986. Частка вуглецю в карбонiтридi зростає в мiру його видiлення (рисунок 5.3 а), але до 910 ЊС, залишається низькою. Нижче 702 ЊС вiдбувається видiлення TiC. Вiд 910 до 702 ЊС можливе видiлення карбонiтридiв промiжних складiв але їх кiлькiсть незначна (рисунок 5.3 б).

Нижче 909 ЊС видiляється Zr (C, N). Вiд 909 до 748 ЊС N переважає над C, але склад зi зниженням температури змiнюється вiд ZrC_0,005N_0,994 до ZrC_0,077N_0,922. Нижче 653 ЊС видiляється ZrC. Змiна вмiсту Zr в твердому розчинi в перiод охолодження вiд 909 до 653 ЊС незначна: вiд 0,0010 до 0,00094%. При температурах нижче 653 ЊС, кiлькiсть Zr в твердому розчинi зменшується, витрачаючись на утворення карбiду.

Кiлькiсть карбiдiв i нiтридiв Zr становить близько 11 мг на 1 кг сталi. На рисунку 5.3 (в) представлена дiаграма, що показує маси сполук Zr в 1 кг металу, що видiлилися в рiзних температурних iнтервалах. Основна частина сполук Zr в сталi зазначеного складу видiляється у виглядi карбiду в феритнiй областi.

Нiтриди i карбонiтриди V в зазначених умовах не видiляються, тому що до моменту початку видiлення VC (нижче 514 ЊС) азот вже пов'язаний в високотемпературнi нiтриди i карбонiтриди. Кiлькiсть VC, що видiлиться складає ~ 0,67 г / кг.

Як видно з дiаграм на рисунку 5.2, кiлькiсть сполук одного i того ж карбонiтрiдоутворюючого елементу, що видiляється за температурний iнтервал зi змiною температури змiнюється не плавно, а спадаючi до малих значень при зниженнi температури; потiм при певному її значеннi рiзко зростає i потiм знову знижується.

У таблицi 5.1 представленi температурнi iнтервали видiлення i кiлькостi карбонiтридiв i карбiдiв, що видiляються в данiй сталi. Так, в 1 кг сталi зазначеного складу в рiвноважних умовах при кiмнатнiй температурi мiститиметься ~ 1,57 г карбiдних i нiтридних фаз.

а)

б)

Рисунок 5.3 - Змiна частки карбiдної складової в карбонiтридi Ti (а) i вмiсту Ti в твердому розчинi (б) в мiру зниження температури

Виконано цiлий ряд подiбних модельних дослiджень i для сталей iншого складу. Зокрема, показано вплив вмiсту Ti (0,000...0,015%) на склад карбонiтридiв V i Nb.

Таблиця 5.1 - Склади, температурнi iнтервали видiлення i маса карбонiтридiв i карбiдiв, що видiляються в сталi 08Г2МФБ

5.3 Термодинамiчне моделювання карбонiтрiдоутворення в комплексно мiкролегiровангних сталях в iзотермiчних умовах

Значний практичний iнтерес представляє опис видiлення карбонiтридних фаз з об'ємi твердого розчину в iзотермiчних умовах [146]. У роботi карбонiтридна фаза розглядається як взаємна рiвновага всiх карбiдiв i нiтридiв, що видiляються i спiвiснують при данiй температурi. Отриманий результат є усередненими по об'єму металу.

Розглянемо сталь наступного складу: С - 0,1%, Mn - 0,45%, Si - 0,25%, Al - 0,03%, Ti - 0,015%, Nb - 0,03%, V - 0,05 %, N - 0,005%. Припустимо, всi цi елементи в початковий момент входять до складу твердого розчину в зазначенiй кiлькостi. З них в утвореннi карбiдiв можуть брати участь Ti, Nb i V, в утореннii нiтридiв - Ti, Nb, V i Al. На рисунку 5.4 представлена система графiкiв, що вiдображає спiввiдношення мiж масами карбiдiв i нiтридiв рiзних елементiв, що утворилися в сталi даного складу при рiзних температурах. З представлених даних видно, що при високих температурах (понад 1000 ®С) переважає нiтрид нiобiю. При зниженнi температури видiлення його частка падає, поступаючись його карбiду. Подiбний характер носить спiввiдношення мiж карбiдом i нiтридом титану. Частка нiтриду алюмiнiю серед цих сполук плавно зростає вiд 3,9% при 1150 ®С до 10,4% при 770 ®С. Частка карбiдiв i нiтридiв ванадiю, що видiляються при розглянутих температурах в сталi даного складу мала.

На рисунку 5.5 представлена залежнiсть рiвноважної сумарної маси карбiдiв i нiтридiв, що видiлилися в залежностi вiд температури. Маса карбiдiв зростає в мiру зниження температури видiлення. Вiд 1150 до 1000 ®С кiлькiсть нiтридiв зростає, при бiльшому зниженнi температури iзотермiчної витримки маса нiтридiв, що видiляються, дещо знижується. Вище температури приблизно 970 ®С в карбонiтриднiй фазi переважають нiтриди, при бiльш низькiй температурi - карбiди. Сумарна маса карбонiтридних фаз змiнюється вiд 1,54 г/т при 1150 ®С до приблизно 640 г/т при 770 ®С.

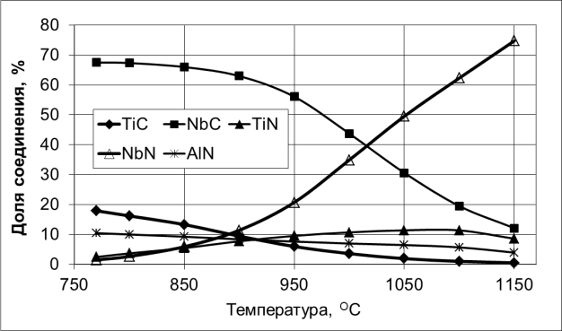
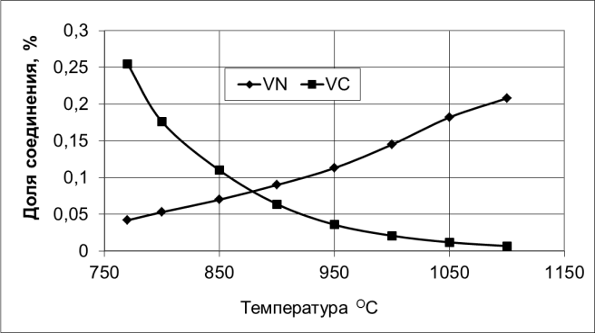
а) б)

Рисунок 5.4 - Спiввiдношення мiж карбiдами i нiтридами

Ti, Nb, Al (а) i V (б), що видiляються при рiзних температурах

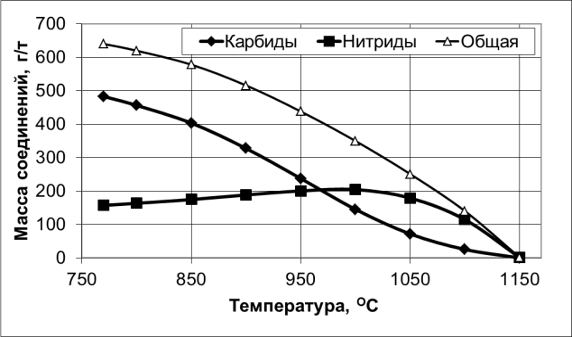
Рисунок 5.5 - Маса карбiдної i нiтридної складової карбонiтридних фаз в залежностi вiд температури видiлення

Розглянемо вплив на видiлення карбiдiв i нiтридiв вмiсту карбонiтрiдоутворювачiв в межах: Al - 0...0,06%, Ti - 0...0,35%, Nb - 0...0,06%. Вплив кожного iз зазначених елементiв дослiджувався окремо, при цьому значення вмiсту iнших елементiв зафiксовано на серединах даних iнтервалiв [148].

Вплив алюмiнiю. На рисунку 5.6 представленi залежностi частки TiC (а), NbC (б), TiN (в), NbN (г), AlN (д) в карбонiтриднiй фазi вiд вмiсту в сталi алюмiнiю. Зi збiльшенням вмiсту алюмiнiю зростає частка TiC. При високих температурах (1100 ЊС) цей вплив незначний, але росте з її зниженням. Аналогiчний характер впливу алюмiнiю i на частку NbC: до 0,01...0,02% Al спостерiгається помiтне зростання частки даного карбiду, подальше збiльшення його вмiсту лише незначно пiдвищує частку даного карбiду.

Характер впливу алюмiнiю на частку нiтридiв титану i нiобiю iнший, а саме, з ростом концентрацiї алюмiнiю спостерiгається її зниження. З рисунка 5.6 (в) видно, що при високих температурах (1100 ЊС) вплив алюмiнiю на частку нiтриду титану практично вiдсутнiй (всi змiни знаходяться в межах помилки розрахунку). Зниження частки TiN при збiльшеннi вмiсту алюмiнiю стає бiльш вираженим у мiру зниження температури iзотермiчної витримки i при вiдносно низьких температурах асимптотично наближається до нуля.

Частка AlN зростає в мiру збiльшення концентрацiї Al. Змiна температури впливає на форму цiєї залежностi. При високих температурах (1100 ЊС) залежнiсть практично лiнiйна. У мiру зниження температури спостерiгається бiльш помiтна змiна частки AlN при низьких вмiстах алюмiнiю (до 0,2...0,3%) i зменшення її зростання у мiру подальшого збiльшення концентрацiї алюмiнiю.

а) б)

в) г)

д)

Рисунок 5.6 - Вплив алюмiнiю на склад карбонiтридної фази при

рiзних температурах видiлення

а)

б)

в)

Рисунок 5.7 - Вплив алюмiнiю на масу карбiдiв i нiтридiв, що видiляються при рiзних температурах: а) 1100 ЊС; б) 950 ЊС; в) 800 ЊС

На рисунку 5.7 представленi результати розрахунку впливу Al на масу карбiдiв i нiтридiв, що видiляються при рiзних температурах. При високих температурах видiлення вплив алюмiнiю на маси карбiдiв i нiтридiв незначний (рис. 5.7 а). Зниження температури сприяє формуванню бiльш виражених залежностей. Зростання вмiсту Al призводить до зниження маси нiтридних i зростанню маси карбiдних видiлень, що формуються при 950 i 800 ® С.

Таким чином, Al крiм утворення AlN може помiтно впливати на формування карбiдiв i нiтридiв титану i нiобiю, що особливо проявляється при зниженнi температури видiлення.

Вплив титану. На рисунку 5.8 представленi залежностi частки TiC (а), NbC (б), TiN (в), NbN (г), AlN (д) в карбонiтриднiй фазi вiд вмiсту в сталi Ti. Змiна вмiсту титану впливає i на частки карбiдiв i нiтридiв всiх елементiв. З рисунка 5.8 (б) слiдує, що при 1100 ЊС i 950 ЊС збiльшення вмiсту титану призводить до деякого збiльшення частки карбiду нiобiю, при подальшому зниженнi температури видiлення спостерiгається зворотний характер впливу - помiтне зниження частки карбiду нiобiю при зростаннi вмiсту титану.

Зi зростанням вмiсту Ti вiдбувається зниження частки NbN. Найбiльша залежнiсть спостерiгається при пiдвищених температурах, а при 800 ®С вплив незначний. Характер змiни частки AlN вiд вмiсту титану якiсно аналогiчний NbN: при пiдвищених температурах залежнiсть слабо виражена i зростаюча, при пiдвищеннi температури - бiльш помiтна i спадна.

На рисунку 5.8 показано вплив вмiсту титану на масу карбiдiв i нiтридiв, що видiляються при рiзних температурах. З наведених графiкiв видно, що збiльшення концентрацiї титану при всiх температурах призводить до зростання як загальної маси надлишкових фаз, так i маси карбiдiв. Маса нiтридiв залежить в першу чергу вiд температури. Змiна вмiсту титану призводить на неї лише незначний вплив, бiльш виражений при пiдвищених температурах i майже вiдсутнє при знижених. При 1100 ЊС для всiх розглянутих концентрацiй титану спостерiгається переважання нiтридної фази. При 950 ®С переважання нiтридiв, що має мiсце при вмiстi титану менше 0,01% змiнюється переважанням карбiдiв. При 800 ®С зростаюче переважання фази карбiду над нiтридною спостерiгається при всiх концентрацiях титану.

Особливий iнтерес представляє вплив вмiсту Ti на частки NbC i AlN. У розглянутих випадках, при змiнi температури вiдбувається змiна характеру залежностi (при бiльш високих температурах - зростання, при бiльш низьких - спадання). Змiна вмiсту титану впливає головним чином на кiлькiсть (масу) карбiдiв, в той час як вплив його на масу нiтридiв незначний.

Вплив нiобiю. На рисунку 5.10 представлена залежнiсть частки TiC (а), NbC (б), TiN (в), NbN (г), AlN (д) вiд вмiсту в сталi Nb. Збiльшення вмiсту нiобiю призводить до зниження частки як карбiдiв, так i нiтридiв Ti. Зростання вмiсту Nb веде також до зниження частки AlN. Залежнiсть частки NbN вiд вмiсту Nb в сталi (рисунок 5.10 г), має максимум, помiтний при пiдвищених температурах. При пiдвищеннi вмiсту Nb починає спостерiгається нестача азоту, необхiдного для подальшого збiльшення кiлькостi утворюваних нiтридiв.

Прирiст маси нiтридiв зi зростанням концентрацiї нiтрiдоутворюючого елемента сповiльнюється. Зi збiльшенням вмiсту Nb, маса його карбiдiв продовжує зростати. Бiльш наочно описаний ефект видно на рисунку 5.11, на якому представлено вплив Nb на масу карбiдiв i нiтридiв. Загальна частка карбонiтридної фази при всiх розглянутих температурах зростає зi збiльшенням концентрацiї Nb.

Зростає головним чином маса карбiдiв. Зростання маси нiтридiв спостерiгається при пiдвищених температурах. Саме такий характер спiввiдношення змiн "швидкостей" зростання мас карбiдної i нитридної складових i призводить до формування вищезгаданого екстремуму на рисунку 5.10 (г). Зниження температури призводить до нiвелювання залежностi маси нiтридiв вiд вмiсту Nb, залежнiсть маси карбiдiв вiд його концентрацiї наближається до лiнiйної. Це викликає розмиття максимуму на графiку 5.10 (г) для бiльш низьких температур.

а) б)

в) г)

д)

Рисунок 5.8 - Вплив титану на склад карбонiтридної фази при рiзних температурах видiлення

а)

б)

в)

Рисунок 5.9 - Вплив титану на масу карбiдiв i нiтридiв, що видiляються при рiзних температурах: а) 1100 ЊС; б) 950 ЊС; в) 800 ЊС

а) б)

в) г)

д)

Рисунок 5.10 - Вплив нiобiю на склад карбонiтридних фази при рiзних температурах видiлення

а)

б)

в)

Рисунок 5.11 - Вплив нiобiю на масу карбiдiв i нiтридiв, що видiляються при рiзних температурах: а) 1100 ЊС; б) 950 ЊС; в) 800 ЊС

Наведенi вище результати можуть надавати iстотну допомогу при виборi режиму термiчної або термомеханiчної обробки сталей, що мiстять карбонiтрiдоутворюючi елементи. З одного боку, для призначення температури деформацiї i / або температури iзотермiчної витримки для видiлення необхiдної кiлькостi змiцнювальної фази (карбiдiв i нiтридiв) заданого складу. З iншого боку, для визначення температури нагрiвання пiд термообробку, коли необхiдний зворотний процес - перехiд легуючих елементiв iз зв'язаного в розчинений стан при збереженнi деякої кiлькостi карбонiтридної фази для стримування зростання зерна.

5.4 Вплив вмiсту цирконiю на карбонiтрiдоутворення в мiкролегованiй низьковуглецевiй сталi

Цирконiй в сталях є сильним карбонiтродоутворювачем, але в данiй роботi вiн розглянутий також в дещо iншому аспектi, а саме з урахуванням його здатностi впливати на процеси видiлення сполук iнших елементiв, при утвореннi карбонитриду Zr витрачаються C, N i сам Zr; отже вiдбувається перерозподiл C i N мiж карбо- i нiтрiдоутворюючими елементами i змiнюються умови видiлення їх сполук.

Як приклад розглянемо сталь 10Г2ФБ наступного складу: С - 0,08%, Mn - 1,48%, Si - 0,25%, S - 0,004%, P - 0,011%, Cr - 0,04%, Ni - 0 , 03%, Cu - 0,06%, Ti - 0,013%, Al - 0,03%, Nb - 0,032%, V - 0,064%, N - 0,007%. Розрахуємо процеси видiлення карбонитридiв при рiзних вмiстах Zr: 0% (гiпотетичний випадок повної вiдсутностi в сталi домiшки Zr); 0,001%; 0,005%; 0,010% [148].

На рис. 5.12 (а) представленi графiки змiни складу карбонитриду Nb у мiру його видiлення в процесi охолодженнi металу. При вiдсутностi в сталi Zr або при дуже низькому його вмiстi (~ 0,001%) на кривiй змiни складу є максимум i мiнiмум. Такий хiд кривих пояснюється високою чутливiстю карбонитриду нiобiю до змiни спiввiдношення вмiстiв Nb i N в твердому розчинi, яке формується процесами видiлення його власних карбонитридiв i сполук Ti i V.

До певного моменту N з твердого розчину витрачається на утворення карбонитридiв Nb та Ti. Зниження його концентрацiї призводить до зростання карбiдної частки в карбонiтридi Nb. При температурах близько 1000...900 ЊС значна частина Ti зв'язується в карбонiтриди з сильним переважанням нiтридної складової. Iнтенсивнiсть їх видiлення падає (рис. 5.12 (б), зменшується i витрата N на їх утворення.

а)

б)

Рисунок 5.12 - Вплив Zr на температурну залежнiсть складу карбонитридiв Nb (а) i на характер змiни вмiсту Nb в твердому розчинi (б)

Внаслiдок зазначених процесiв, в певний момент спiввiдношення N, C i Nb в твердому розчинi починає змiнюватися так, що вiдносна частка карбiдної складової в карбонiтридi нiобiю починає падати . Це виражається максимумом на кривiй. З початком видiлення карбонитридiв V азот починає йти на їх утворення, що провокує нове зростання карбiдної складової в карбонiтридi Nb. З представленої на рис. 5.12 (а) системи кривих видно, що вплив Zr на змiну складу карбонитридiв Nb є досить iстотним. Навiть невеликий вмiст Zr (~ 0,001%) збiльшує частку карбiдної складової в карбонiтридi Nb (особливо в середньому iнтервалi температур). При вмiстi Zr 0,005% i бiльше, внаслiдок того, що частина N зв'язується в карбонiтриди Zr , в нижньому iнтервалi температур можливе видiлення NbC.

З рис. 5.12 (б) видно, що Zr в сталi майже не впливає на змiну iнтенсивностi i видiлення карбонитридiв Nb. Велика частина Nb зв'язується в карбонiтриди при температурах понад 1000 ®С; кiлькiсть бiльш низькотемпературних карбонитридiв i/або карбiдiв є малою. Розрахунки показали, що при 0,010% Zr маса високотемпературних (1326...1037 ЊС) карбонитридiв Nb складе ~ 393 мг/кг, маса NbС, що видiлився нижче 890 ЊС складає приблизно 8,3 мг / кг. Кiлькiсть низькотемпературних карбiдiв Nb має тенденцiю зростати з пiдвищенням вмiсту Zr: так при меншому його вмiстi (0,005%) кiлькiсть їх становить всього ~ 2,6 мг / кг.

Вплив Zr на видiлення карбонитридiв Ti, показаний на рисунку 5.13, має дещо iнший вигляд. При вiдсутностi або вкрай низькому вмiстi Zr, титан утворює карбонiтрид з сильним переважанням карбiдної складової (приблизно TiC_0,999 N_0,001).

При пiдвищеному вмiстi Zr забирає на себе частину азоту i при низьких температурах можливе утворення TiС (рис. 5.13 а). Зi збiльшенням концентрацiї Zr менша частка Ti зв'язується в високотемпературний нiтрид i росте частка карбiду (рис. 5.13 б). При вмiстi Zr 0,005%, як показують розрахунки, кiлькiсть карбонитриду Ti з нiтрiдним переважанням становить ~ 159 мг/кг, а карбiду трохи бiльше 8 мг/кг, при збiльшеннi вмiсту Zr до 0,010% кiлькiсть високотемпературних нiтридiв Ti складе ~ 137 мг/кг, а карбiду ~ 29 мг / кг. Iз зростанням змiсту Zr, спадання концентрацiї Ti в твердому розчинi за рахунок нiтрiдоутворення стає бiльш плавним, а температура початку видiлення TiC збiльшується.

а)

б)

Рисунок 5.13 - Вплив Zr на температурну залежнiсть складу карбонитридiв

Ti (а) i на характер змiни змiсту Ti в твердому розчинi (б)

Вплив Zr на видiлення сполук V є не настiльки сильним. Можна лише вiдзначити, що при низькому його вмiстi можливе утворення деякої кiлькостi бiльш високотемпературного карбонитриду V (рис 5.14).

Кiлькiсть цього карбонитриду, що видiляється при температурах ~ 780...525 ЊС є незначною i становить ~ 14 мг/кг, тодi як кiлькiсть бiльш низькотемпературних карбiдiв складає при цьому ~ 728 мг/кг (при повнiй вiдсутностi Zr). При 0,005% Zr утворення карбонитридiв V моделлю не передбачається. Подальше збiльшення вмiсту Zr до 0,010% не робить значного впливу на процеси утворення VC.

а)

б)

Рисунок 5.14 - Вплив Zr на температурну залежнiсть складу карбонитридiв V (а) i на характер змiни змiсту V в твердому розчинi (б)

Слiд зазначити, що цирконiй сам також утворює карбонiтриди. При низькому його вмiстi (0,001%), як показують результати математичного моделювання, в складi карбонитриду переважає нiтрiдна складова, а температурний iнтервал видiлення становить 1166...827 ЊС. З пiдвищенням концентрацiї Zr температура початку видiлення його сполук зростає до 1329 ЊС при 0,005% i 1378 при 0,010%. При цьому частка карбiдної складової в ньому зростає i стає можливим видiлення карбiду цирконiю при температурах нижче 533 ЊС при 0,005 % Zr i нижче 608 ЊС при 0,010 % Zr.

Таким чином, методом математичного моделювання проведено аналiз впливу рiзних концентрацiй Zr на процеси карбонiтридоутворення в сталi 10Г2ФБ. Розрахованi температурнi iнтервали видiлення карбонiтридiв Nb, Ti, V i Zr; показана змiна їх складу i визначена частка карбiдної складової в карбонiтридах, що видiляються. Встановлено, що наявнiсть в сталi Zr призводить не тiльки до утворення власних карбонiтридiв, а й певним чином впливає на видiлення сполук iнших карбо- i нiтрiдоутвроючих елементiв. А саме, спостерiгається значний вплив Zr на склад карбонiтридiв Nb i змiна iнтенсивностi видiлення нiтридiв Ti. Пiдвищення вмiсту Zr в сталi 10Г2ФБ здатне iнiцiювати видiлення деякої кiлькостi практично чистих низькотемпературних карбiдiв Nb i Ti i пригнiчити видiлення вiдносно високотемпературних карбонитридiв V. Показано, що Zr в сталi, крiм утворення власних спецiальних карбiдiв i нiтридiв, може бути використаний для керування процесами видiлення карбонитридiв основних мiкролегiрующiх елементiв.

Таким чином, нами встановлено зниження температури видiлення карбонiтридних фаз, яке обумовлене витратою азоту, титану i нiобiю на утворення бiльш високотемпературних нiтридiв, а також розподiлом азоту мiж декiлькома елементами.

На прикладi сталей 08Г2МФБ i 10Г2ФБ промодельований процес утворення карбонiтридiв i карбiдiв. Встановлено, що в сталi 08Г2МФБ можливе утворення двох типiв сполук одних i тих же елементiв: високотемпературних карбонитриду нiобiю складу NbC_0,38N_0,61...NbC_0,99N_0,01; карбонитриду титану складу TiC_0,0013N_0,9986...TiC_0,019N_0,988 i бiльш низькотемпературних їх сполук з переважанням карбiдної складової.

На прикладi мiкролегованої низьковуглецевої сталi, що мiстить (Al - 0,03%, Ti - 0,015%, Nb - 0,03%, V - 0,05%) розрахованi усередненi склади карбонiтридної фази, кiлькiсть карбiдiв i нiтридiв, залишковi концентрацiї розчинених в металi Al, Ti i Nb в залежностi вiд температури iзотермiчної витримки. Показано, зниження рiвноважних часток нiтридiв i збiльшення часток карбiдiв титану та нiобiю при зменшеннi температури iзотермiчної витримки. При цьому також спостерiгається зростання частки нiтриду алюмiнiю.

Визначено екстремальний характер залежностi частки NbN вiд вмiсту Nb в сталi, особливо добре виявляється при пiдвищених температурах видiлення. Показано iстотне зниження частки нiтридiв титану i алюмiнiю при зростаннi концентрацiї нiобiю, а також частки карбiду титану (тiльки при вiдносно знижених температурах iзотермiчної витримки).

РОЗДIЛ 6

Термiчна обробка низьколегованих сталей у потоцi повiтря з керованою швидкiстю

6.1 Базовi принципи керування охолодженням за рахунок змiни швидкостi потоку повiтря

Охолодження на нерухомому повiтрi - це досить повiльний i неконтрольований процес. Швидкiсть охолодження може бути збiльшена, якщо привести повiтря в рух (створити повiтряний потiк). У той же час, змiна швидкостi потоку повiтря може регулювати iнтенсивнiсть вiдтоку тепла. Структура матерiалу, утворена пiд час процесiв термiчної обробки, залежить вiд швидкостi охолодження. Таким чином, змiнюючи швидкiсть потоку охолоджувального середовища, можна регулювати структуру матерiалу виробу.

Основним типом теплообмiну в системi, що складається з металевого зразка i рухомого повiтря, є конвекцiя. Цей процес можна описати законом охолодження Ньютона, в якому зазначено, що швидкiсть втрати тепла з фiзичного тiла прямо пропорцiйна рiзницi температур мiж тiлом та його оточенням за умови, що рiзниця температур невелика, а природа випромiнюючої поверхнi залишається однаковою. Закон охолодження Ньютона в конвекцiї є перестановкою диференцiального рiвняння, заданого законом Фур'є:

(6.1)

де: Q - теплова енергiя, J; ? - коефiцiєнт теплопередачi, W/(m²"K); А - площа поверхнi теплопередачi, м²; ?T (t) - градiєнт температури мiж середовищем та об'єктом, К.

Змiна середньої температури зразка по мiрi втрати теплової енергiї, яка дорiвнює Q, становить:

(6.2)

де: T - температура зразка, К; C_p - питома теплоємнiсть, J/(кг"К); m - маса зразка, кг.

Рiвняння (6.2) можна використовувати для грубої оцiнки змiни температури зразка, коли його розмiри досить малi. Для великих зразкiв слiд враховувати рiвняння теплопровiдностi для нестацiонарного стану. Але навiть для цього випадку рiвняння (6.2) можна використати для розрахунку втрат тепла з приповерхневого шару методом скiнчених рiзниць. Поєднуючи рiвняння (6.2) та (6.1), ми можемо отримати диференцiальне рiвняння для оцiнки змiни температури пiд час процесу охолодження у невеликому зразку (6.3):

(6.3)

Основним завданням конвективних задач є пошук коефiцiєнта теплопередачi ?. Для цього використовується число Нуссельта. Коефiцiєнт теплопередачi дорiвнює (6.4):

(6.4)

де: Nu - число Нуссельта; ? - коефiцiєнт теплопровiдностi, W/(m"K); d - характерний розмiр, м.

Число Нуссельта залежить вiд числа Рейнольдса i числа Прандтля. Ця залежнiсть виражається емпiричною формулою, яка має наступний вигляд (6.5):

(6.5)

де: Re - число Рейнольдса; Pr - число Прандтля;
,
, n - емпiричнi параметри.

Число Рейнольдса сильно залежить вiд швидкостi руху середовища (6.6):

(6.6)

де: v - швидкiсть руху навколишнього середовища, м/с; d - гiдравлiчний дiаметр, м; ? - кiнематична в'язкiсть, м²/с.

Слiд зауважити, що бiльшiсть параметрiв залежать вiд температури.

З рiвнянь вище видно, що швидкiсть охолодження залежить вiд швидкостi руху середовища через залежнiсть вiд числа Рейнольдса. Таким чином, змiна швидкостi потоку повiтря може використовуватися для управлiння швидкiстю охолодження.

6.2. Конструкцiя лабораторної установки для контрольованого повiтряного охолодження

На основi вищеописаного принципу розроблено i побудовано лабораторний автоматичний пристрiй для керованого повiтряного охолодження. Схема цього пристрою наведена на рисунку 6.1.

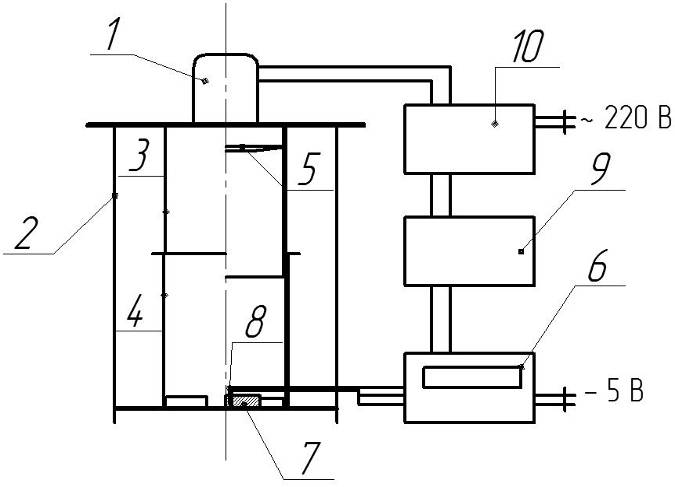
Рисунок 6.1 - Принципова схема керованого автоматичного пристрою повiтряного охолодження

1 - двигун постiйного струму;

2 - несучий корпус;

3 - верхня (фiксована) частина трубки робочої камери;

4 - нижня (рухома) частина трубки робочої камери;

5 - вентилятор;

6 - контролерний блок;

7 - охолоджуваний зразок;

8 - датчик температури;

9 - симисторний регулятор;

10 - силовий блок i випрямляч

Пристрiй для керованого охолодження виробiв у повiтряному потоцi мiстить камеру для охолодження, вентилятор з електричним двигуном постiйного струму, що дозволяє регулювати швидкiсть обертання. Робоча камера являє собою розсувну трубу з двох частин, у верхнiй частинi якої розмiшено вентилятор. Повiтря виходить з камери через прогалини в нижнiй i бiчнiй стiнках. Привiд вентилятора - це електричний двигун постiйного струму, швидкiсть якого автоматично регулюється електронною схемою з мiкроконтролером за рахунок широтно iмпульсного керування електричним струмом вiдповiдно до заданої програми. Контролер вiдповiдно до заданої програми на основi даних про змiну швидкостi потоку повiтря, якi зчитуються з текстового файлу, розмiщеного на картi пам'ятi SD, генерує керованi прямокутнi електричнi iмпульси з амплiтудою 5 В певної ширини i частоти.

Ширина iмпульсу розраховується програмою, вставленою на контролер, на основi даних про часовий iнтервал i необхiдну швидкiсть потоку повiтря. Iмпульси подаються до симисторного блоку. Вiн складається з двох ступенiв. Перша ступiнь - це оптрон, який забезпечує повну гальванiчну розв'язку струмiв, контролера та блоку живлення. Це захищає контролер вiд перешкод з мережi електроживлення та перешкод, викликаних роботою двигуна. Друга ступiнь - це регулятор потужностi. Електричний струм випрямляється випрямлячем. Симiсторний регулятор за допомогою низької напруги керує високою напругою, як ключ реле, але здатний працювати на набагато бiльш високiй частотi. Таким чином, на електродвигун постiйного струму подають iмпульсну напругу з амплiтудою 220 В. Це еквiвалентно зменшенню напруги, що дозволяє двигуну обертатися з меншою швидкiстю. Двигун обертає вентилятор, який створює потiк повiтря у робочiй камерi. Камера - це труба, яка складається з двох вставлених одна в одну частин, якi можна зсунути / розсунути. Це необхiдно для спрощення розмiщення в ньому охолоджуваного виробу. Перед тим, як класти гарячий вирiб, слiд пiдняти верхню частину труби, а потiм опустити її назад. Труба в нижнiй частинi спирається на металеву (сталеву) пластину, яка має отвори. На бiчнiй поверхнi труби внизу розташованi щiлини. Чим швидше буде потiк повiтря, тим iнтенсивнiше буде охолодження. Данi щодо поточного потоку та часу вiд початку процесу вiдображаються на дисплеї контролера. Термопара або датчик температури з пiдсилювачем, який можна вставити в охолоджуваний вирiб, пiдключається до контролера. Сигнал термопари надходить у контролер. На його основi розраховується значення температури. Вiн вiдображається на дисплеї контролера та записується у файл, розташований на картi пам'ятi SD. Цей файл створюється на початку процесу i мiстить данi у виглядi пар час/температура. Процес завершується, коли програма контролера досягає останнього рядка в файлi iнструкцiй або пiсля натискання кнопки передчасного переривання на контролерi. Файл з вихiдними даними може бути створений як вручну, так i бути розрахованим i створеним за допомогою спецiальної комп'ютерної програми, яка реалiзує математичну модель охолодження металевого зразка в повiтряному потоцi. Iнодi важко привести датчик температури до виробу, який охолоджується на досить високiй швидкостi, не пошкоджуючи вирiб. Тому передбачено режим роботи без зворотного зв'язку.

Пристрiй має такi конструктивнi особливостi. Для фiксацiї нижньої половини труби у верхньому положеннi нижня поверхня верхньої кришки має спецiальнi петельки, а труба має вiдповiднi "вуха". Контролер та схеми управлiння розташованi в окремому корпусi. Контролер має незалежне джерело живлення 5 В. Програма в контролерi враховує нелiнiйнiсть залежностi швидкостi потоку повiтря вiд застосовуваної ширини керуючих iмпульсiв.

6.3 Експериментальне дослiдження режимiв керованого повiтряного охолодження

Для експерименту з термiчної обробки за допомогою охолодження у керованому потоцi було взято 3 типи зразкiв з низько- и середньо вуглецевої сталi. Хiмiчний склад зразкiв наведено в таблицi 6.1.

Таблиця 6.1 - Хiмiчний склад зразкiв (мас. %)

Зразки являли собою паралелепiпеди з отвором дiаметром 5 мм для термопари. Середнi розмiри та маси зразкiв наведенi в таблицi 6.2.

Таблиця 6.2 - Середнi розмiри та маси зразкiв

Початкова термiчна обробка всiх цих зразкiв була нормалiзацiєю, яка включає в себе нагрiвання до 900 ЊC i охолодження на нерухомому повiтрi. Час нагрiву для зразкiв типу 1 становив ~ 15 хвилин, для типу 2 ~ 20 хвилин, а для типу 3 ~ 30 хвилин. Пiсля цiєї попередньої термiчної обробки середня твердiсть зразкiв була наступною:

тип 1 - 81,5 Ђ 3,6 HRB

тип 2 - 81,1 Ђ 3,3 HRB

тип 3 - 73,8 Ђ 1,1 HRB

Типовi мiкроструктури зразкiв показанi на рисунку 6.1.

Чисельнi характеристики (середнiй розмiр зерна та перлiтових колонiй) мiкроструктури матерiалу зразкiв:

тип 1 - 14,3 Ђ 3,9 мкм

тип 2 - 20,1 Ђ 5,2 мкм

тип 3 - 34,4 Ђ 9,6 мкм

Виходячи з розрахунку за допомогою нашого застосування для моделювання кiнетики фазового перетворення та програми для обчислення конвекцiйного теплообмiну, були розробленi режими охолодження для кожного типу зразкiв. Також були розрахованi режими змiни швидкостi потоку повiтря в умовах охолоджуючого пристрою для реалiзацiї цих режимiв. Дiаграми режимiв показанi на рисунку 6.2. Реалiзовано хвилеподiбну змiну швидкостi потоку повiтря для усунення рiзницi температур в поперечних перерiзах зразкiв. Розробленi методики спрямованi на отримання феритових (у низьковуглецевiй сталi) та феритоперлiтних структур з бiльш дрiбним зерном.

Змiна структури була помiчена у всiх зразках пiсля контрольованого швидкого охолодження. Типовi структури показанi на рисунку 6.3.

Структура зразкiв типу 1 i 2 пiсля термообробки стала бiльш перлiтною. Колонiї перлiту стають дрiбнiшими, а феритнi прошарки тонше. Це вiдбувається тому, що режими охолодження призводять до того, що перлiтне перетворення вiдбувається при бiльш низьких температурах. Бейнiтовi структури не було виявлено. Змiна структури зразкiв типу 3 (низьковуглецева сталь) не настiльки значна, однак було помiчене деяке подрiбнення феритового зерна. Чисельнi характеристики змiни середнього розмiру зерна показано в таблицi 6.3.

a) b) c)

d) e) f)

g) h) i)

Рисунок 6.1 - Структура зразкiв пiсля попередньої нормалiзацiї,

збiльшення в 487: a, b, c - тип 1; d, e, f - тип 2; g, h, I - тип 3

a)

b)

c)

Рисунок 6.2 - Режими охолодження зразкiв:

а) для типу 1, b) для типу 2, c) для типу 3

Середнє подрiбнення зерна в зразках є наступним:

тип 1 - 2,26 рази тип 2 - 2,11 разiв тип 3 - 1,32 рази

Слiд зауважити, що середнє подрiбнення розмiрiв зерна майже пропорцiйно вмiсту вуглецю та обернено пропорцiйно масi зразкiв.

Виконано також вимiрювання твердостi. Показано деяке збiльшення середнього значення твердостi. Ступiнь збiльшення твердостi була рiзною в рiзних типах зразкiв, i не корелює напряму з середнiм подрiбненням зерна. Чисельну змiну середньої твердостi показано в таблицi 6.4.

Таблиця 6.3 - Порiвняння середнього розмiру зерна

зразкiв до i пiсля обробки

Таблиця 4. - Складання зразкiв середньої твердостi до i пiсля обробки

Середнiй рiвень твердостi в зразках збiльшується наступним чином:

тип 1 - 1,09 разiв

тип 2 - 1,11 разiв

тип 3 - 1,07 разiв

З'ясувалося, що збiльшення твердостi залежить не тiльки вiд ступеня зменшення розмiрiв зерна, але i вiд вмiсту Mn. Таким чином, пiдвищенний вмiст Mn у зразках типу 2 призводить до значнiшого збiльшення значень твердостi порiвняно з типом 1.

Таким чином, було побудовано лабораторний автоматичний пристрiй повiтряного охолодження. Вiн використовувався для дослiдження розроблених режимiв охолодження низько- i середньовуглецевих сталей. Вивченi режими показали значне перероблення структури сталi, яка також стає бiльш перлiтною у зразках середньо-вуглецевої сталi.

a) b) c)

d) e) f)

g) h) i)

Рисунок 6.3 - Структура зразкiв пiсля контрольованого повiтряного охолодження, збiльшення в 487: a, b, c - тип 1; d, e, f - тип 2; g, h, I - тип 3

Вимiряно числовi характеристики структури. Змiна структури призводить до збiльшення твердостi. Але це збiльшення не залежить вiд тiльки вiд подрiбнення зерна. Виявлено вплив Mn на твердiсть у розроблених методах контрольованого повiтряного охолодження. Запропонованi технологiї регулювання повiтряного охолодження можуть бути корисними для полiпшення характеристик структури дрiбних металевих виробiв iз середньовуглецевих сталей, особливо з високим вмiстом Mn. Але вони менш ефективнi для низьковуглецевих сталей.

РОЗДIЛ 7

Основи методологiї аналiзу даних i виявлення прихованих залежностей

Значний об'єм корисної iнформацiї можна отримати не тiльки з безпосереднiх заздалегiдь спланованих експериментiв, але з аналiзу накопичених даних. Це можуть бути промисловi данi вимiрювань виконаних в ходi технологiчних процесiв, данi лабораторних дослiджень контролю якостi. Можливо також агрегування i спiвставлення результатiв експериментiв, зроблених рiзними дослiдниками у рiзний час. Таке дослiдження не завжди є простим спостереженням, у ньому можуть переслiдуватися певнi цiлi i задачi пошуку iмовiрної закономiрностi, що передбачена теорiєю, доведення або спростування певних конкретних гiпотез. В такому разi говорять про так званий пасивний експеримент. Накопичення в нашi часи великих об'ємiв даних i швидке зростання їх кiлькостi привело до актуалiзацiї подiбних пiдходiв i створення таких понять, як Data Science та Big Data.

Методологiя подiбних дослiджень розвивається давно i має в своїй основi апарат статистичного аналiзу. Класичними пiдходами, вiдомими багатьом дослiдникам є кореляцiйний, лiнiйний i нелiнiйний регресiйний аналiзи, порiвняння середнiх значень, дисперсiйний аналiз, дослiдження функцiй розподiлу. Цi методи знаходять широкий пiдхiд при аналiзi ефективностi впроваджень, побудовi емпiричних моделей, виявленнi причин браку або, навпаки, несподiвано гарних результатiв.

Не слiд забувати про задачi кластерiзацiї даних. Це є вiдшукання певних розмежованих груп у сукупностi, що розглядається. Групи отриманi подiбним чином можуть вважатися обґрунтованими i нештучними. Так, їх iснування може свiдчити про механiчне об'єднання рiзнорiдних даних в одну сукупнiсть. Метод дозволяє в такому випадку об'єктивно роздiлити цi данi. Також таким чином можна виявити несподiване роздiлення результатiв експерименту на декiлька розмежованих груп.

Далi коротко розглянемо загальнi вiдомостi про багатофакторний регресiйний аналiз, кластеризацiю, їх поєднання i методи пiдготовки даних до статистичної обробки.

7.1 Багатофакторний регресiйний аналiз

Зазвичай на дослiджуваний показник або властивiсть впливає декiлька факторiв. Регресiйний аналiз є загальновiдомим пiдходом, що дозволяє оцiнити значущiсть впливу певних факторiв на властивiсть, що розглядається, i побудувати емпiричну модель для передбачення значень цiєї властивостi з певною вiрогiднiстю.

Сутнiсть регресiйного аналiзу у загальному випадку зводиться до вiдшукання значень коефiцiєнтiв аналiтичного виразу певного виду, при яких результати обчислення цiльового показника (властивостi) будуть якомога близькими до реально спостережуваних у при пiдстановцi в нього вiдповiдних наборiв значень факторiв. Вибiр загального виду рiвняння, що найточнiше описує залежнiсть, що розглядається є складною задачею. В тих випадках, коли iснує фiзичне обґрунтування певного виду залежностi можна використовувати вiдповiднi функцiї, можливо пiдбирання навмання функцiй рiзних типiв, але це є довгим i не завжди продуктивним пiдходом. Тому за замовчуванням, в бiльшостi випадкiв, принаймнi у якостi першого наближення використовують лiнiйнi рiвняння. Використання лiнiйних функцiй виправдано тим, що така функцiя вказує напрям впливу (принаймнi на розглянутiй дiлянцi), при малому iнтервалi варiювання нелiнiйнi ефекти можуть суттєво не даватися взнаки, окрiм того багато нелiнiйних функцiй можна звести до лiнiйних, наприклад шляхом логарифмування значень факторiв. Таким чином, найпоширенiшим є лiнiйний регресiйний аналiз.

Загальний вигляд рiвняння лiнiйної регресiї наступний (7.1):

(7.1)

де F - розраховане значення дослiджуваної властивостi, x_n - значення факторiв, a_n - емпiричнi коефiцiєнти рiвняння регресiї

Значення коефiцiєнтiв рiвняння регресiї знаходять методом найменших квадратiв на пiдставi масиву значень факторiв i дослiджуваної властивостi.

Кожний коефiцiєнт визначає ступiнь впливу вiдповiдного фактора на показник, залежнiсть якого розглядається. Але у загальному випадку реальних задач фактори можуть бути рiзнорiдними i мати рiзний порядок характерних значень. Наприклад, вмiст компонентiв визначається у вiдсотках (тобто нормований на 100), розмiр мiроструктурних складових у мiкрометрах, а температура має значення сотнi чи тисячi градусiв. Тому порiвнювати коефiцiєнти вiдповiдно до характеристики ступеню впливу факторiв у їх натуральних масштабах важко i не зовсiм коректно. З цiєю метою значення факторiв i властивостi масштабуються, зазвичай нормуються на одиницю. Так, при однаковому умовному масштабi факторiв легше порiвняти коефiцiєнти i зiставити їх вплив з характерною похибкою, тобто визначити значущiсть впливу кожного з факторiв.

Лiнiйнi рiвняння регресiї є простим i поширеним пiдходом. Вони зазвичай годяться для оцiнки впливу, але не завжди дають результат передбачення значень дослiджуваної властивостi з необхiдною точнiстю. Причина лежить у нелiнiйностi багатьох реальних залежностей. В таких випадках можливе введення у рiвняння нелiнiйних елементiв. Найбiльш простими i поширеними є фактори у певних ступенях: квадрати, куби, -1 ступiнь тощо, можливi i iншi, наприклад логарифмiчнi або експоненцiальнi компоненти. Зазвичай для цього обчислюється ряд значень певного фактору до якого застосували задану нелiнiйну функцiю. Цей ряд значень використовується як новий окремий фактор. Вiдповiдно задача нелiнiйної регресiї зводиться до лiнiйної. Iншим випадком появи нелiнiйностi є наявнiсть корельованих мiж собою факторiв. Такi фактори можна ввести у рiвняння не окремо, а у виглядi їх добутку - ефект взаємодiї. Обчислення ряду їх добуткiв сприймається як значення нового фактору i задача регресiї також зводиться до лiнiйної.

Слiд зазначити, що для формального розв'язання задачi з пошуку коефiцiєнтiв рiвняння регресiї кiлькiсть вимiрювань (наборiв значень) повинна бути не меншою, нiж кiлькiсть факторiв у наборi. Для побудови статистично значущої моделi, що враховує похибку на вплив випадкових i невiдомих факторiв кiлькiсть вимiрювань потрiбна значно перевищувати кiлькiсть параметрiв (факторiв).

7.2 Кластерний аналiз

Трапляються випадки за яких вихiднi данi у просторi факторiв i властивостей розподiленi не рiвномiрно i можна говорити про певнi вiдокремленi групи (кластери) даних. Наприклад у наявнiй сукупностi переплутано представленi данi по декiльком рiзним маркам сталi, що мають рiзний вмiст легуючих елементiв. Сталей, що мають промiжнi мiж наявними значення вмiсту легуючих елементiв у вибiрцi немає. Очевидно, що кожну марку бiльш коректно було б розглянути окремо. Iнодi треба вирiшити дещо iншу задачу: встановити коректнiсть штучного роздiлення дослiджуваної сукупностi даних на певнi групи. Тобто на скiльки точно реальнi кластери спiвпадають з запропонованими групами.

Задача тiльки на перший погляд здається простою i очевидною. Зазвичай у просторi великої кiлькостi факторiв, перетасованих наборiв значень i апрiорної невiдомостi про наявнiсть у вибiрцi декiлькох окремих груп кластери з першого погляду буває побачити досить важко. Iнодi причиною роздiлення вихiдних даних на кластери може бути вплив деякого неврахованого фактору, або певного спiввiдношення мiж вiдомими факторами, про вплив якого заздалегiдь невiдомо.

На даний час розроблено цiлий ряд алгоритмiв кластерного аналiзу. Серед них метод K-середнiх i його модифiкацiя - нечiтка кластеризацiя C-середнiх, графовi алгоритми, статистичнi алгоритми, алгоритми сiмейства FOREL, EM-алгоритм, нейронна мережа Кохонена та деякi iншi. Найбiльш простим i широко застосованим є алгоритм K-середнiх. Незважаючи на деякi його очевиднi недолiки вiн є прийнятний для бiльшостi задач. Саме цей алгоритм застосовувався у наших дослiдженнях (роздiл 8).

Алгоритм K-середнiх був винайдений у 1950-х роках Гуго Штайнгаузом i Стюартом Ллойдом i розвинений Джеймсом МакКвiном. Коротко його сутнiсть можна описати наступним чином. Метод базується на мiнiмiзацiї суми квадратiв вiдстаней мiж кожним спостереженням та центром його кластера, тобто функцiї (7.2):

(7.2)

де d - метрика, x_i - i-ий об'єкт даних, a, m_i(x_i) - центр кластера, якому на j-iй iтерацiї приписаний елемент x_i.

Визначається очiкувана кiлькiсть кластерiв. Знаходяться центри кластерiзацiї (центроїди). Для знаходження центроїдiв спочатку випадково обирається k-спостережень, якi на цьому кроцi вважаються центрами кластерiв. Потiм уточнюється положення центроїдiв яке розраховується як середнє арифметичне ознак об'єктiв, що входять у iмовiрний кластер. Так вiдбувається то тих пiр, поки центри кластерiв не стануть стiйкими. Центроїд кожного з кластерiв на кожнiй наступнiй iтерацiї стає новим середнiм. Дисперсiя в серединi кластеру мiнiмiзується, а мiж кластерами максимiзується. Якщо кiлькiсть кластерiв апрiорно невiдома, то рекомендують провести дослiдження з рiзною кiлькостi очiкуваних кластерiв i потiм порiвняти результати.

Метод має наступнi недолiки:

- результат вiдшукання кластерiв залежить вiд випадкових початкових позицiй кластерних центрiв;

- наявнiсть викидiв у масивi вихiдних даних може викривляти положення центроїдiв кластерiв

- кiлькiсть кластерiв, на якi проводиться розподiл повинна визначається дослiдником.

Незважаючи на означенi недолiки, головною перевагою методу k-елементiв є його простота i швидкiсть виконання. Отриманi результати зазвичай цiлком задовольняють вимоги.

7.3 Попередня пiдготовка даних i регресiйний аналiз на кластерах

Багатофакторний регресiйний аналiз здатний оцiнити ступiнь i напрям впливу кожного з факторiв на дослiджувану властивiсть i побудувати емпiричну модель. Але як згадувалося вище, данi можуть бути з тих чи iнших причин неоднорiднi i мiшанi. Також можуть даватися взнаки вплив неврахованих з тих чи iнших причин факторiв Це може призвести до приховування залежностей, що мають мiсце у вибiрцi.

Наведемо простий приклад з однiєю ознакою (фактором) i однiєю властивiстю. Задачею є встановлення залежностi мiж ними. Вибiрка, представлена в таблицi 7.1.

Таблиця 7.1 - Приклад вихiдних даних

Апроксимацiя лiнiйною функцiєю дає наступне рiвняння (7.3):

Y = 3,7445 + 0,6565"X (7.3)

Але отримана аналiтична залежнiсть має досить низький коефiцiєнт детермiнацiї R² = 0,1311. З цього можна зробити висновок, що залежнiсть мiж показниками X та Y виражена дуже слабко i статистично незначуща. Але цей висновок є насправдi хибним. Подивимося на розташування точок у координатнiй площинi та на положення апроксимуючої прямої, що наведено на рисунку (7.1):

Рисунок 7.1 - Розташування точок з модельного

прикладу i апроксимуюча пряма

Таблиця 7.1 - Роздiлення на два кластери

даних з модельного прикладу

З наведеної iлюстрацiї видно, що точки можна роздiлити принаймнi на двi окремi групи. Тобто ми маємо справу з дещо мiшаними даними. Такi данi можна подiлити на два кластери, що представленi у таблицi 7.2.

З графiкiв i наведених значень показника R² на рисунку 7.2 видно, що роздiлення даних на два кластери показало iснування досить суттєвих залежностей мiж показниками X та Y в кожному з них.

Рисунок 7.2 - Розташування точок з модельного прикладу: апроксимацiя проведена по кластерах

Так, можливо, переносячись до iмовiрних подiбних реальних випадкiв, у кластерi 1 додатково дiяв якийсь неврахований фактор, що сприяв значному пiдвищенню показника Y по мiрi зростання показника X. В той же час у вибiрцi, що вiдiйшла до кластеру 2 подiбний фактор не дiяв, тому залежнiсть вийшла бiльш пологою.

Таким чином ми бачимо, як кластерний аналiз дозволяє знайти прихованi залежностi, а також замислюватися над причиною вiдмiнностi поводження груп даних, що на перший погляд здавалися однорiдними, шукати неврахованi фактори (можливо, якiснi), що притаманнi випадкам що увiйшли до певних кластерiв.

Для проведення регресiйного аналiзу на кластерах була розроблена невелика комп'ютерна програма (скрипт) на мовi Python. При написаннi програми задiянi бiблiотеки numpy, scipy, sklearn та mathplotlib. Вихiднi данi беруться з файлу MS Excel. Оскiльки кiлькiсть очiкуваних кластерiв вважається невiдомою, вiдбувається поетапне розбиття вибiрки на рiзну кiлькiсть кластерiв вiд 2 до 10. Але максимальна кiлькiсть кластерiв не може бути бiльшою нiж загальна кiлькiсть рядкiв даних подiлена на 5. Тобто, у разi, якщо у нас, наприклад тiльки 16 рядкiв даних то їх буде подiлено тiльки на 2 i 3 кластери, а якщо, наприклад, 21, то на 2, 3 i 4 кластери. Це зроблено для уникнення розбивання на маленькi неiнформативнi кластери у випадку невеликої вибiрки.

Для проведення кластеризацiї данi пiддаються спецiальнiй пiдготовцi. Всi фактори i властивостi центруються вiдносно математичного очiкування (яке приймається за 0) i нормуються на Ђ1. Потiм транспонована матриця вихiдних даних помножується на себе нетранспоновану. В результатi отримуємо симетричну квадратну матрицю, кiлькiсть рядкiв i колонок у якiй дорiвнює загальнiй кiлькостi факторiв i властивостей. Для отриманої матрицi обчислюються власнi вектори. Цi вектори утворюють багатомiрний базис. У базисi цих власних векторiв перераховуються вектори (строки) значень вихiдної таблицi. Саме на пiдготовлених таким чином даних виконується алгоритм кластеризацiї. При цьому, для кластеризацiї можуть бути вiдiбранi тiльки деякi з iснуючих параметрiв (факторiв). Потiм проводиться для кожного кластера перевiд його у iстинi значення i до них додаються вiдповiднi значення параметрiв (факторiв i властивостей), за якими кластеризацiя не проводилася. Данi кластерiв зберiгаються у окремих файлах MS Excel.

Наступним кроком є проведення регресiйного аналiзу на даних, що були видiленi в окремi кластери. Для проведення регресiйного аналiзу вiдбираються не всi кластери, а тiльки тi, кiлькiсть рядкiв даних у яких бiльше кiлькостi факторiв i в будь якому разi на менше 5. Можливе автоматичне проведення регресiйного аналiзу залежностi цiлого ряду властивостей вiд одного набору факторiв. Результати розрахункiв рiвнянь багатофакторної лiнiйної регресiї вiдповiдно до розглянутихх властивостей i кластерiв зберiгаються у окремому файлi MS Excel. Зберiгаються данi не по всiх властивостях i кластерах, а тiльки тi, в яких коефiцiєнт детермiнацiї рiвняння регресiї перевищує 0,5. Це зроблено для автоматичного вiдсiювання кластерiв i властивостей, по яким не виявлено чiтких залежностей.

Таким чином, розроблена програма дає змогу вiдшукати прихованi залежностi мiж властивостями i факторами i автоматизувати процес вiдбору досить великих кластерiв i кластерiв, на яких отримано чiткi залежностi. В подальшому розроблена програма була задiяна для аналiзу причин крихкого руйнування евтектоїдних сталей.

РОЗДIЛ 8

Розробка методiв пiдвищення пластичностi i протидiї крихкому руйнуванню у евтектоїдних сталях

8.1 Пiдвищення показникiв вiдносного звуження сталi загартованих рейок

Iснує чимало дослiджень, присвячених вдосконаленню технологiї виробництва рейок i пiдвищенню їх якостi. Сучасним i високоефективним способом змiцнення є поверхневий гарт головки рейок струмами високої частоти з охолодженням водно-повiтряною сумiшшю або стисненим повiтрям. Розроблено технологiї, що дозволяють змiцнювати не тiльки верхню, але i бiчну поверхню головки рейки. Чимало уваги придiлялося також пiдвищенню якостi рейкової сталi i оптимiзацiї її хiмiчного складу. Iснують також дослiдження спрямованi на зниження негативного впливу на властивостi рейкової сталi неметалевих включень. Слiд зазначити, що основна маса розробок була спрямована на пiдвищення мiцностi, твердостi, зносостiйкостi рейок, тодi як питання полiпшення пластичних властивостей (вiдносного подовження i звуження) дослiджувалися недостатньо. При вдосконаленнi технологiї виробництва рейок увага придiляється не тiльки забезпеченню високих механiчних властивостей металу, а й зниженню кiлькостi дефектiв, що утворюються в процесi їх виготовлення. У зв'язку зi зростанням вiдсортовування рейок через незадовiльнi значення ? i пiдвищенням частоти виявлення поверхневих дефектiв на ПАТ "МК" Азовсталь" питання з'ясування причин зазначених проблем i пошук шляхiв їх вирiшення набули високу актуальнiсть [149, 150].

Для виробництва залiзничних рейок типу Р65 на металургiйному комбiнатi "Азовсталь" застосовується сталь конверторної виплавки марки К76Ф, хiмiчний склад якої наведено в таблицi 8.1.

Таблиця 8.1 - Хiмiчний склад рейкової сталi марки К76Ф

У таблицi 8.2 представленi як необхiднi згiдно з чинними ТИ i ТУ механiчнi властивостi даної сталi, так i фактичнi пiсля термообробки (ТВЧ гарту вiд температур 900 - 950 ®С i самовiдпуска при температурi 420 - 480 ®С).

Таблиця 8.2 - Механiчнi властивостi рейкової сталi пiсля термообробки

Як випливає з наведених даних, мiцнiсть, твердiсть, вiдносне подовження i ударна в'язкiсть, як правило, вiдповiдають дiючим вимогам, в той же час, вiдносне звуження варiює в широких межах i нерiдко виявлялося значно нижче необхiдного рiвня. Кiлькiсть партiй рейок з незадовiльним (<25%) значенням ? в перiод з 28.02.2011 по 25.09.2011 було дуже велике i становило близько 40% вiд продукцiї, що випускається, а максимум розподiлу припадав на критичнi значення (? = 24...27%) [149].

Методи оптичної металографiї не дозволяли виявити суттєву рiзницю в мiкроструктурi металу з задовiльними i незадовiльними значеннями ?. Таким чином, для бiльш глибокого дослiдження причин виникнення провалiв по ? були задiянi сучаснi методи тонких металофiзичних дослiджень, такi як просвiча i растрова електронна мiкроскопiя, мiкрорентгеноспектральний аналiз, Оже-спектроскопiя [150].

За допомогою просвiчуючого електронного мiкроскопа JEM-100CXII при прискорюючiй напрузi 100 кВ методом фольги були проведенi детальнi дослiдження мiкроструктури перлiту, результати яких представленi на рисунку 8.1. Тонкi фольги готували з дiлянки робочої частини зразкiв за стандартною методикою: вирiзанi фрагменти утоняются механiчно до товщини 0,12 мм, потiм за допомогою електроiскровий установки з них вирiзали диски дiаметром 3 мм, якi в подальшому пiддавали двосторонньому електролiтичному струменевому полiруванню на установцi "TENUPOL2" виробництва фiрми "STRUERS". Електролiт мав наступний склад: 40 мл хлорної кислоти, 400 мл метилового спирту, 240 мл бутилового спирту. Температура електролiту пiд час полiрування пiдтримувалася за допомогою термостата на рiвнi менше мiнус 30 ®С.

Дослiдження тонкої фольги, приготованої вiд зразкiв обох типiв, показало, що в зразках з ? > 25% мiкроструктура має рiвноважний характер, цементiтниi пластинки добудованi. Мiжпластиночна вiдстань перлiту лежить в iнтервалi 0,13 - 0,19 мкм. У зразках з ? < 25% дiлянок виродженого перлiту бiльше, а мiкроструктура має нерiвноважний характер, який проявляється в незавершеностi цементитних пластин через брак вуглецю. Причиною цього може бути нерiвномiрний розподiл вуглецю в аустенiт i недостатнiсть часу i температури для його дифузiйного перерозподiлу [150].

а) б) в) г)

Рисунок 8.1 - Мiкроструктура рейкової сталi (просвiча електронна мiкроскопiя, в 19808): а, б - ? > 25%; в, г - ? <25%;

Рентгенографiчнi дослiдження показали взаємозв'язок значень вiдносного звуження з розширенням лiнiї 110 фериту. Встановлено, що, чим вище значення вiдносного звуження, тим менше ширина лiнiї. Так, для зразкiв з ? = 15% розширення лiнiї 110 становить 0,21 град., з ? = 25% - 0,189 град., а з ? = 31% - 0,100 град. Крiм того, спостерiгається збiльшення параметра гратки фериту для зразкiв з низькими значеннями ?: а_фер. = 0,28717 нм для зразкiв з ? = 31%, а для зразкiв з ? = 15% а_фер. = 0,28790 нм. Збiльшення параметра решiтки може бути наслiдком пiдвищеного вмiсту вуглецю. За допомогою програмного забезпечення LEASQUAR проаналiзованi профiлi лiнiї 110 для зразкiв з рiзним ?. Встановлено вiдхилення в малих кутах профiлю цiєї лiнiї вiд гаусова розподiлу для зразкiв з ? = 15%. Однiєю з можливих причин такого вiдхилення може бути наявнiсть залишкового аустенiту, що вказує на незавершенiсть ферито-перлiтного перетворення.

Поверхня руйнування зразкiв була дослiджена з використанням растрової електронної мiкроскопiї. Мiкрофотографiї зламiв (збiльшення в350) наведенi на рисунку 8.2, а результати мiкрорентгеноспектрального аналiзу з зазначених дiлянок данi в таблицi 8.3 [150].

а) б)

Рисунок 8.2 - Типовi поверхнi руйнування розривних зразкiв:

а - ? < 25 %; б - ? >25 %

Таблиця 8.3 - Результати мiкрорентгеноспектрального аналiзу

з поверхнi руйнування для дiлянок зазначених на рисунку 45

Кожевенное мастерство | Сайт "Художники" | Доска об'явлений "Книги"