Принцип экстремума полного действия
Оглавление
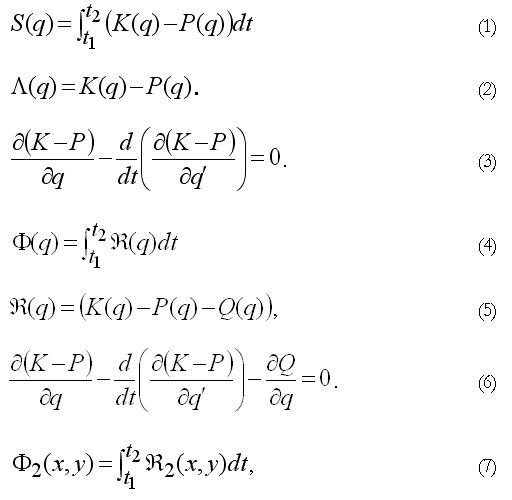
|
|
||
Предлагается новый вариационный принцип экстремума полного действия, который расширяет лагранжев формализм на диссипативные системы. Показывается, что этот принцип применим в электротехнике, механике с учетом сил трения и электродинамике. Предлагаемый вариационный принцип может рассматриваться как новый формализм универсального метода вывода физических уравнений, а также как метод решения этих уравнений. Формализм состоит в построении функционала с единственной седловой линией, уравнение которой и является уравнением динамических переменных для определенной области физики. Метод решения состоит в поиске глобальной седловой линии при заданных условиях физической задачи. | ||
Принцип экстремума полного действия
Оглавление
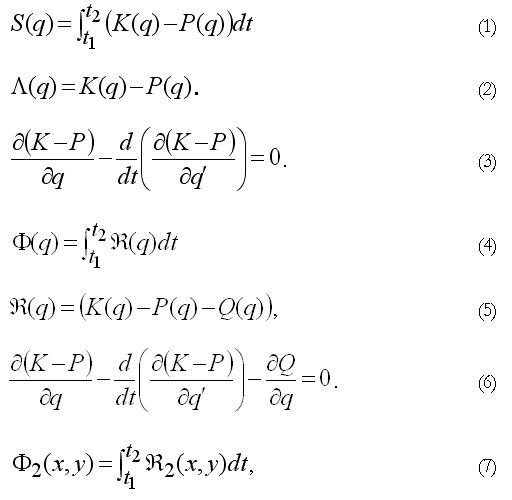
|