|
1) максимальная скорость сигнала одинакова во всех системах отсчёта; 2) Вселенная имеет начало во времени;
3) Вселенная изотропна и однородна.
|
Эти три идеи были хорошо известны в начале XX века; поэтому, например, Лоренц, постулировав утверждение 1, мог бы легко прийти к расширяющейся Вселенной и закону Хаббла — если бы зашел в ближайшую церковь, мечеть или синагогу и поинтересовался насчёт утверждения 2 :) Шутка, в которой есть лишь доля шутки, а истина в ней такая: идеями, существующими не одну тысячу лет, не следует пренебрегать, даже если кажется, что... Да какая разница, что кажется? Не надо ими пренебрегать в любом случае.
Найдем функцию R(v), описывающую поведение тел во Вселенной, в которой справедливы утверждения 1, 2 и 3, а именно функцию зависимости расстояния от скорости.
Поскольку максимальная скорость сигнала не бесконечна (равна скорости света), наблюдатель видит события, происшедшие А лет назад, на расстоянии А световых лет. Если эти А лет прошли с момента возникновения Вселенной, то наблюдатель увидит происшедшее в тот момент событие («событие начала») на расстоянии А световых лет. Чем больше лет от начала времени, тем больше световых лет до «сферы», где мы видим это начало. Таким образом, на основании утверждений 1 и 2 легко прийти к выводу: Вселенная расширяется, и расширяется одинаково во всех направлениях с максимальной скоростью сигнала.
Заметим, что этих двух утверждений достаточно для такого вывода; в моделях Фридмана «чуть» сложнее, правда? Заметим также, что мы говорим о «событии начала», а не о «событиях начала» (след этого одного события удаляется от нас во всех направлениях, что и не удивительно: оно удаляется со скоростью света, а «для света нет системы отсчета»).
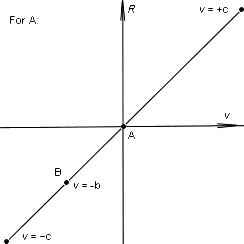
Пусть расстояние до упомянутой сферы равно Rmax. Мы уже получили первую точку графика искомой функции:
R(c) = Rmax.
А вот вторая: любой наблюдатель движется относительно самого себя с нулевой скоростью, его расстояние от самого себя равно нулю:
R(0) = 0
Теперь перейдем к «начинке» между 0 и с. Поскольку мы положили, что Вселенная изотропна (все направления во Вселенной равноправны), искомая функция не может быть разной для разных направлений. Для удобства забудем на некоторое время, что максимальная скорость сигнала не бесконечна (потом мы начисто вычеркнем пройденный ложный путь). Пусть для наблюдателя А движение «начинки» (включая объект В) описывается некой функцией R(v). А так как мы положили, что Вселенная однородна (все места во Вселенной равноправны), то следует считать, что для наблюдателя В движение «начинки» (включая объект А) описывается той же функцией. То есть, мы имеем дело с банальным параллельным переносом осей таким, что начало координат переносится в другую точку, принадлежащую графику, и при этом переносе график должен перейти сам в себя.
Этому условию удовлетворяет не любая функция, а лишь единственный класс функций, линейные функции R(v) = kv + b; но мы знаем, что R(0) = 0; поэтому b = 0, R(v) = kv. Поскольку неважно, как мы обозначаем константу, перепишем: R = v/H0, или, собственно,
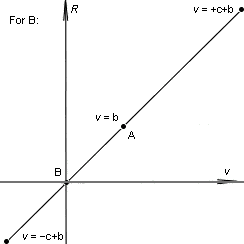
Но нет, не всё. Вспомним то, что мы «забыли»: искомая функция определена только на промежутке [-с; +с] . Получится, что график ни одной функции не переходит сам в себя при параллельном переносе координат, более того, меняется область определения функции:
|
|
Для В функция оказывается определенной в промежутке
Эта невозможность выводит нас на правильный путь: мы (неявно) использовали Галилеево правило сложения скоростей, что делать было нельзя. Используем вместо правила Галилея правило Лоренца. По Лоренцу
Таким образом, закон Хаббла доказан «на бумаге», причем без применения громоздкого аппарата ОТО. Честно говоря, я не вижу здесь даже СТО: постулат Лоренца — это постулат Лоренца, хоть он и включен в СТО. Отдельно отмечу, что это не наезд на СТО; просто для того, чтобы вывести — не пронаблюдать, а вывести — закон Хаббла, было достаточно данных еще до создания этой теории Эйнштейном.
А под конец скажу, что утверждение 3 справедливо не для всех систем отсчета. И вот тут то...