Лабораторная работа
"Измерение скорости футбольного мяча
методом баллистического маятника"
(максимально возможная адаптация для младшей школы)







|
|
||
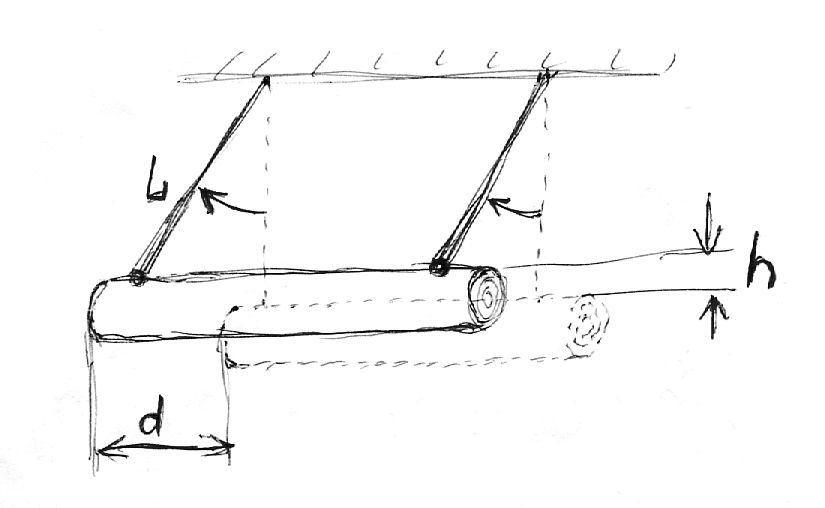
В школе третьекласснику задали "провести научную работу". Сейчас все больше уроков проводят по схеме "Папа у Васи силен в математике" - ученики выходят к доске и бубнят дурацкие "доклады", скачанные родителями из интернета. Это называется "учитель должен не учить, а направлять любознательность ребенка". Как я понимаю - диверсия по развалу системы образования. Я, разумеется, из интернета скачивать не стал - прикололся самостоятельно :) | ||
Лабораторная работа
"Измерение скорости футбольного мяча
методом баллистического маятника"
(максимально возможная адаптация для младшей школы)








|