ВЕЛИКАЯ ТЕОРЕМА ФЕРМА НЕ ВЕРНА
ИМЕЮТСЯ ЕЕ РЕШЕНИЯ СРЕДИ БЕСКОНЕЧНЫХ ЦЕЛЫХ ЧИСЕЛ
ТЕОРЕТИЧЕСКИ ДОКАЗАТЬ ЕЕ НЕ ВОЗМОЖНО
А. М. Белов


В 1670 году было опубликовано математическое утверждение, ставшее известным под названием Последней, Большой или Великой теоремы Ферма, смысл которой состоит в том, что не существует целых значений x, y, z удовлетворяющих уравнению
при условии, что n - целое положительное число, причем n>2, а x, y, z не равны нулю. При этом было сделано утверждение, что Пьер Ферма якобы нашел простое доказательство своего утверждения, но, к сожалению, оно было утеряно.
С тех пор не удается получить общее и понятное любому человеку со средними способностями доказательство этого утверждения. Пока удалось лишь получить очень "умное" более чем на сотню страниц доказательство, которое способна понять горстка избранных. Все это не способствует появлению особого доверия к подобному доказательству. Ведь речь идет не о религии, где достаточно просто верить священнослужителям и при этом ни требовать, ни доказательств, ни тем более понимания и полного познания, а о математике в, которой, как известно, никаких тайн и запретов на познаваемость в принципе не предусматривается.
Все, наблюдавшиеся в течение нескольких веков, попытки найти утерянное доказательство способствуют укреплению мысли о том, что воспроизвести доказательство не удается не потому, что Пьер Ферма был самым избранным среди избранных, а потому, что он, скорее всего, ошибся и его последняя теорема просто не верна, т. е. целочисленные решения, приведенного выше уравнения, все же существуют.
Известно, что Великая теорема Ферма проверялась при помощи ЭВМ для очень больших значений x, y, z, n и при этом целочисленных ее решений найдено не было, что указывает на необходимость проведения поиска решений для случая очень больших чисел, которые на ЭВМ обрабатывать пока невозможно.
Поскольку здесь приводится не доказательство Великой теоремы Ферма, а ее опровержение, состоящее фактически из трех чисел, то тем, кому не интересно читать описание о том, как и на основе каких рассуждений, были получены эти числа, сразу можно продолжить чтение с формул (3,4).
В целях поиска целочисленных решений среди больших чисел проведем следующие преобразования в уравнении (1):
При умножении каждого члена уравнения (1) на одно и то же число равенство будет оставаться верным. Так как необходимо найти целочисленные решения уравнения, то для по членного умножения уравнения нужно подобрать такое число при умножении, на которое любой десятичной дроби, в т. ч. и бесконечной в результате получалось бы целое число. Здесь рассматривается десятичная дробь в связи с тем, что практически любое число, в том числе простые дроби и иррациональные числа представляются в виде десятичных конечных или бесконечных дробей.
Поскольку десятичная дробь есть дробь, знаменатель которой есть целая степень числа 10, то, очевидно, что в качестве такого числа можно использовать число 10 возведенное в бесконечно большую степень ![]() или, иначе говоря, бесконечное произведение числа 10
или, иначе говоря, бесконечное произведение числа 10 ![]() . Число 10 необходимо возводить именно в бесконечно большую степень по той причине, что бесконечная десятичная дробь есть дробь, знаменатель которой есть число 10 возведенное в бесконечно большую степень.
. Число 10 необходимо возводить именно в бесконечно большую степень по той причине, что бесконечная десятичная дробь есть дробь, знаменатель которой есть число 10 возведенное в бесконечно большую степень.
Используя известное правило о том, что произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин и используя выражение (2) можно записать следующие формулы для вычисления целочисленных решений Великой теоремы Ферма:
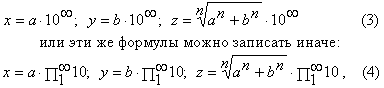
где а и b -практически любые действительные положительные числа.
Анализ формул (3,4) очень быстро приведет к выводу, что Великая теорема Ферма имеет бесконечно большое количество решений среди бесконечных целых чисел.
Далее приведен ряд конкретных примеров значений x, y, z, являющихся целочисленными решениями уравнения (1), которые были получены за счет применения формул (3,4). Существование лишь одного подобного примера опровергает Великую теорему Ферма.
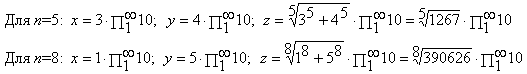
Записать, приведенные выше числа в обычном виде не представляется возможным, не хватит никакой бумаги и никаких чернил и на ЭВМ обработать их так же невозможно, их даже записать в ЭВМ не удастся, так как никакой памяти не хватит. Поэтому для того, что бы получить хоть какое то представление о том, как эти числа выглядят в обычном виде, ниже приведены записи фрагментов этих чисел с начальной их части.
Для n=5: x=300000000...; y=400000000...; z=417402766...
Для n=8: x=100000000...; y=500000000...; z=500000159...
Тем же, кто привык все проверять своими руками на калькуляторе в качестве утешения можно предложить при помощи ниже приведенных формул пронаблюдать сходимость к точному решению приведенных решений уравнения (1) при постепенном приближении произведения числа 10 к бесконечному произведению.
![[]](/img/b/below_a_m/ab13/9.gif)
где [ ] - знак, обозначающий целую часть числа, т.е. от результата вычисления выражения, заключенного в скобки [ ] необходимо отбросить дробную часть числа, а с оставшейся целой частью продолжать вычисления.
При k равном бесконечности формулы (5) будут полностью соответствовать формулам (3,4) и F1 будет точно равно F2, а при всех меньших значениях k F1 будет равно F2 лишь приближенно. Причем чем больше будет k, тем меньше будут отличаться F1 и F2, что демонстрирует приведенный ниже пример для случая a=2, b=3, n=3.
k=0 F1=35 F2=27 отклонение F1 от F2 22,8571... %
k=1 F1=35000 F2=32768 отклонение F1 от F2 6,3771... %
k=2 F1=35000000 F2=34965783 отклонение F1 от F2 0,0977... %
k=3 F1=35000000000 F2=34997871511 отклонение F1 от F2 0,00608... %
...............................................................................................
Разумеется, формулы (5) справедливы только, когда a и b являются целыми числами, а n>2.
Если n>2, то при помощи формул (3,4) можно получить одно единственное решение уравнения (1) в целых числах для каждого значения показателя степени n , a и b, а вот если n=2 и a и b соответствуют какому либо решению уравнения (1) в целых числах, то при изменении показателя степени k возведения числа 10 в формулах (3,4) от 0 до бесконечности можно получить бесконечный ряд целочисленных решений уравнения (1). Так, известно, что числа 3; 4; 5 являются решениями уравнения (1) при n=2. Подстановка в формулы (3,4) a=3 b=4 при изменении показателя степени k числа 10 в формулах (3,4) от нуля до бесконечности позволяет получить следующий бесконечный ряд целочисленных решений уравнения (1):
k=0 x=3 y=4 z=5
k=1 x=30 y=40 z=50
k=2 x=300 y=400 z=500
k=3 x=3000 y=4000 z=5000
k=4 x=30000 y=40000 z=50000
k=5 x=300000 y=400000 z=500000
...................................................
Пример бесконечного ряда решений для случая, когда n=2 здесь приведен исключительно для тех, кто хочет убедиться в справедливости формул (3,4) и существовании бесконечно больших решений уравнения (1) в целых числах непосредственно на калькуляторе. Конечно, если терпения хватит, и калькулятор подходящий найдется. Остальные смогут убедить себя в этом и без громоздких вычислений, просто логически рассуждая.
Необходимо отметить, что представление конкретных решений уравнения (1) фактически только в виде формул не является чем-то необычным. Так и только так точно представляются некоторые дроби или иррациональные числа, которые иначе могут быть записаны лишь в виде фрагментов бесконечных десятичных дробей. Например:
Применяя метод бесконечного спуска для доказательства отсутствия решений в целых числах для уравнения x4 + y4 = z4 Ферма начал с предположения о существовании гипотетического решения в целых числах (x1, y1, z1).
При изучении свойств чисел (x1, y1, z1) Ферма показал, что если бы такое гипотетическое решение действительно существовало, то существовало бы меньшее решение (x2, y2, z2). Рассматривая это новое решение, Ферма смог показать, что если бы оно существовало, то существовало бы еще меньшее решение (x3, y3, z3) и так далее.
Ферма обнаружил нисходящую лестницу решений, которая теоретически могла бы продолжаться неограниченно, порождая все меньшие и меньшие решения. Но x, y и z должны быть целыми или натуральными числами, поэтому нескончаемая нисходящая лестница невозможна, потому что должно быть наименьшее целочисленное решение.
Полученное противоречие доказывает, что начальное предположение о существовании решения (x1, y1, z1) было ложным. Итак, используя метод бесконечного спуска, Ферма возможно и предположил, что при n = 4 уравнение xn + yn = zn не может иметь целочисленных решений.
Однако метод бесконечного спуска позволяет доказать существование решений уравнения xn + yn = zn в целых бесконечных числах, так как для любого решения в целых бесконечных числах можно находить до бесконечности меньшие решения в целых бесконечных числах и так никогда и не дойти до наименьшего решения. Поскольку наименьшего решения в целых бесконечных числах просто не существует. Например, для уравнения x4 + y4 = z4 можно записать его решение в целых бесконечных числах:
![[]](/img/b/below_a_m/ab13/11.jpg)
Меньшее решение в целых бесконечных числах можно получить следующим образом:
![[]](/img/b/below_a_m/ab13/12.jpg)
где k - число большее единицы, то есть может последовательно выбираться из ряда натуральных чисел: 2, 3, 4, 5, ... и чем больше по величине будет k, тем меньшими будут решения уравнения x4 + y4 = z4 в целых бесконечных числах (x, y, z). Но поскольку ряд натуральных чисел бесконечный, то и число k можно увеличивать бесконечно, а это означает, что найти наименьшее решение (x, y, z) невозможно.
Таким образом, метод бесконечного спуска может быть применен для доказательства Великой теоремы Ферма только для случая, когда решения уравнения xn + yn = zn выражаются в конечных числах. Но поскольку классическая формулировка Великой теоремы Ферма не содержит данного ограничения, то получается, что она не может быть верной.
Приходилось ли вам читать о бесконечных целых числах или использовать где- либо этот термин? Мне нет и это притом, что представление о бесконечности натурального ряда чисел было сформировано уже в 3 в. до н. э. в трудах Евклида и Архимеда, а, например, используя давно известное бесконечное произведение их легко получить. При этом использование других бесконечных чисел - бесконечных десятичных дробей широко распространено. Чем же они отличаются друг от друга? Дело в том, что если использовать лишь часть бесконечной десятичной дроби, то величина ошибки будет приемлема для их практического использования, а в случае с бесконечными целыми числами в аналогичной ситуации нет. Например, числа 0,333 и 0,3333 выделенные из бесконечной дроби 0,333333... отличаются друг от друга на 0,09%, а числа 333 и 3333 выделенные из бесконечного целого числа 333333... будут отличаться друг от друга на 90%. В масштабах же всего бесконечного целого числа величина ошибки вообще будет бесконечно большой. Таким образом, можно утверждать, что бесконечные целые числа являются самыми бесполезными числами, их совершенно невозможно использовать в практических вычислениях. Поэтому и писать о них вроде как не за чем.
Однако выдающийся немецкий математик создатель теории бесконечных множеств и теории трансфинитных чисел Георг Фердинанд Людвиг Филипп Кантор (3 марта 1845 - 6 января 1918), несмотря ни на что, все же отметил, что реальные бесконечные целые числа относятся к так называемой актуальной бесконечности и образуют бесконечный ряд подобных чисел, которые отличны друг от друга и находятся в закономерных числовых отношениях друг к другу и к конечным целым числам. Более того, исследование абсолютно бесконечного ряда реальных целых чисел привело Кантора к усмотрению в этом ряду так называемых числовых классов. Первый числовой класс есть множество конечных целых чисел: 1, 2, 3, ... За ним следует второй числовой класс. Он состоит из некоторых бесконечных целых чисел, следующих одно за другим в определенной последовательности. Затем идут 3-й, 4-й числовые классы и так далее. Хотя целые бесконечные числа и являются самыми бесполезными, все же Кантор, почему-то просто их проигнорировать не захотел.
В связи с тем, что Ферма умер задолго до рождения Кантора остается открытым вопрос, знал ли он о существовании решений для своей теоремы среди целых бесконечных чисел и вообще о существовании этих чисел?
То, что для опровержения Великой теоремы Ферма потребовалось использовать самые бесполезные, в практическом смысле, числа выглядит весьма символично, так как вообще то Великую теорему Ферма следовало бы назвать самой бесполезной теоремой Ферма. Поскольку сам по себе факт получения доказательства или опровержения этой теоремы ровно никакой ценности в практическом смысле представлять не будет. Конечно, приверженцы теоремы утверждают, что это не важно, важно, то, что она стимулировала развитие математики. Вот только стимулировала ли развитие математики теорема сама по себе или все же это результат ее "раскрутки": объявлений о премиях, шумихи в печати? Ведь, мало ли в математике всяких занимательных и всем понятных задачек? Которые не были "раскручены" и не послужили стимулом для развития математики.
Хотя целые бесконечные числа, получаемые при помощи формул (3,4) и являются бесполезными для целей практического их применения, но при подстановке в формулы (3,4) различных исходных параметров будут получаться в результате и числа разные, которые практически можно сравнивать по величине, что достаточно для целей этой статьи.
Необходимо отметить, что рассматриваемые целочисленные решения уравнения (1) являются потенциальными, но даже такие решения делают теоретически невозможным общее доказательство Великой теоремы Ферма, так как из любого правильного доказательства Великой теоремы Ферма обязательно должно следовать, что уравнение (1) имеет решения в бесконечных целых числах и, как говорят в подобных случаях, круг замкнулся. Конечно, формулировку Великой теоремы Ферма можно изменить, указав в ней, что уравнение (1) не имеет решений только в целых конечных числах x, y, z или договориться без всяких доказательств, что бесконечных целых чисел не существует или, что они являются не целыми и тем самым избавиться от неудобных бесконечных целых чисел. Однако я бы предостерег энтузиастов доказательства Великой теоремы Ферма от попыток ее доказательства в ее обновленном виде, так как в этом случае необходимо будет доказать, что предлагаемое доказательство учитывает все возможные конечные целые числа, т. е. немного ни мало необходимо будет найти границу целых конечных чисел, а, учитывая, что ряд натуральных чисел бесконечен, сделать это даже теоретически вряд ли представляется возможным.
Правда, энтузиастам доказательства Великой теоремы Ферма все же есть польза от приведенных здесь высказываний. Польза состоит в упрощении проверки новых доказательств, да, впрочем, и старых тоже. Если из предложенного доказательства не следует, что уравнение (1) имеет решения среди бесконечных целых чисел, то это однозначно означает, что предложенное доказательство содержит ошибки, причем вне зависимости от того, сколько избранных его одобрили и саму ошибку в этом случае можно уже и не искать, а сразу приступить к составлению нового доказательства. Кроме этого из любого правильного доказательства должна так же еще и следовать теорема Пифагора.
Поскольку Великая теорема Ферма в ее классическом виде не является верной, то, как и следовало ожидать, ничего этого из официально признанного верным доказательства Эндрю Уайлиса 1993-1994 годов вовсе не следует.
В связи с широким распространением информации о доказательстве Уайлиса все же необходимо подробно рассмотреть проблемы данного доказательства.
Доказательство Уайлиса основывается на противоречиях сформулированной в 1955 году молодым японским математиком Ютакой Таниямой следующей гипотезы: всякая эллиптическая кривая с рациональными коэффициентами модулярна. Данная гипотеза относилась к алгебраической геометрии, разделу математики, в котором изучаются геометрические объекты, связанные с алгебраическими уравнениями.
Эллиптической кривой называется кривая на плоскости, заданная уравнением y2 = x3 + a"x2 + b"x + c, где a, b, c - рациональные числа. Уравнения такого вида так же еще называются кубическими.
Проблема эллиптических кривых, как и проблема доказательства Великой теоремы Ферма, заключается в вопросе, имеют ли соответствующие им уравнения целочисленные решения, и если имеют, то сколько.
Модулярная форма представляет собой специфическую функцию очень богатую свойствами симметрии, что позволяет ей преобразовываться самой в себя. То есть модулярные формы можно подвергать трансляциям (параллельным переносам, или сдвигам), перестраивать, переставлять фрагменты, отражать в зеркалах и поворачивать бесконечно многими способами, и при этом они останутся неизменными, что делает их наиболее симметричными математическими объектами.
Ни нарисовать, ни даже вообразить модулярную форму невозможно. Модулярную форму можно представлять как функцию, область определения которой находится в двух измерениях, но и область значений которой также двумерна. Поэтому график такой функции может существовать только в четырехмерном пространстве.
Разумеется, существуют условия модулярности эллиптической кривой, и эти условия слишком сложны, для того чтобы, без дополнительных обоснований, можно было поверить в существование хотя бы одной модулярной эллиптической кривой. Поэтому понятно почему, вначале гипотезу Ютаки Таниямы о том, что абсолютно все эллиптические кривые с рациональными коэффициентами модулярны не принял всерьез ни один профессиональный математик. Тем более что Танияма не смог обосновать наличие связи между теориями эллиптических кривых и модулярных форм, а смог привести лишь серию примеров связанных друг с другом эллиптических кривых и модулярных форм.
Однако постепенно к 1970-м годам усилиями японского математика Г. Шимуры и французского математика А. Вейля удалось получить достаточно серьезные подтверждения гипотезы Таниямы, но строго доказать эту гипотезу они все же не смогли.
Наконец в 1984 году немецкий математик Герхард Фрей указал на возможную связь гипотезы Таниямы с Великой теоремой Ферма. Его рассуждения сводились к следующему.
Пусть Великая теорема Ферма не верна, то есть для какого-то числа n > 2 верно равенство xn + yn = zn в целых конечных числах, то есть A + B = C, где A = xn , B = yn , C = zn.
После этого Фрей преобразовал уравнение Ферма xn + yn = zn с учетом гипотетических его решений к следующему виду:
y2 = x"(x - A)"(x - C) = x3 - (A + C)"x2 + A"C"x.
То есть преобразовал уравнение Ферма xn + yn = zn в кубическое уравнение и тем самым показал, что кривая, соответствующая этому уравнению, является эллиптической.
Сразу необходимо отметить, что существовать эта эллиптическая кривая будет только в том случае, если будут существовать конкретные значения коэффициентов a, b, c. В противном случае эллиптическая кривая просто будет не задана. Так как сам Фрей это обстоятельство никак не пояснял.
Затем он заявил, что эта кривая обладает такими свойствами, что ей никак не может соответствовать какая-либо модулярная форма. Это, в свою очередь, вступает в противоречие с гипотезой Таниямы, согласно которой любая эллиптическая кривая должна соответствовать некоторой модулярной форме. А в результате получается альтернатива: либо эта гипотеза верна, и тогда первоначальное предположение о существовании решения уравнения Ферма не соответствует действительности (а значит, справедлива Великая теорема Ферма), либо рассматриваемая гипотеза не верна. Таким образом, в случае обоснования гипотезы Таниямы автоматически будет получено доказательство Великой теоремы Ферма.
Однако необходимо обратить внимание на существование ряда вопросов к рассуждениям Фрея. Так как на эти вопросы до сих пор никто никаких ответов не дал.
Эллиптическая кривая существует только в том случае, если коэффициенты a, b, c будут выражаться в конкретных числах, а если они не были представлены в виде конкретных чисел, то вне зависимости от причин этого, эллиптической кривой просто нет или можно сказать, что конкретная эллиптическая кривая не была задана. Незаданной эллиптической кривой никак не может соответствовать какая-либо модулярная форма. Если не были заданы ни эллиптическая кривая, ни модулярная форма, то рассматривать в рамках гипотезы Таниямы собственно говоря становится и нечего. Иначе говоря, для того чтобы появились основания для использования гипотезы Таниямы при доказательстве Великой теоремы Ферма необходимо доказать, что объект 'кривая Фрея' действительно является конкретной эллиптической кривой. То есть показать, что конкретные значения коэффициентов a, b, c не гипотетически, а реально существуют, а это сделать невозможно. Ведь контр пример для Великой теоремы Ферма до сих пор никто не нашел (здесь имеется ввиду контр пример в конечных целых числах).
Гипотетически существующей кривой Фрея, если и может соответствовать, то только гипотетическая модулярная форма. И в принципе отсутствуют основания для существования у гипотетической кривой Фрея реальной модулярной формы. Да и гипотеза Таниямы не предусматривает рассмотрение гипотетических кубических уравнений и модулярных форм.
С другой стороны, если доказать, что коэффициенты a, b, c невозможно задать в качестве реально существующих чисел из-за отсутствия соответствующих решений для уравнения Ферма, то зачем доказывать что-то еще? Разве именно не это требовалось для доказательства Великой теоремы Ферма? А именно отсутствие соответствующих решений для уравнения Ферма. И в этом случае гипотеза Таниямы опять оказывается никак не связанной с Великой теоремой Ферма.
По этим причинам рассуждения Фрея выглядят не совсем корректными. Тем не менее, американский математик Кен Рибет обосновывает, что гипотетической кривой Фрея никак не может соответствовать какая-либо модулярная форма. То есть фактически обосновал, что если конкретная эллиптическая кривая не была задана, то не существует и соответствующая ей модулярная форма. Впрочем, разве и безо всяких доказательств не является очевидным, что если нет конкретной эллиптической кривой, то нет и соответствующей ей модулярной формы?
Однако если не обращать внимания на эти проблемы, то для доказательства Великой теоремы Ферма осталось только обосновать гипотезу Таниямы. И в 1986 году англичанин Эндрю Уайлс, который с детства мечтал доказать Великую теорему Ферма и очень кстати ранее специализировался на теории эллиптических кривых, решился приступить к обоснованию гипотезы Таниямы.
Только после нескольких лет напряженной работы, 23 июня 1993 года на Международной математической конференции в Кембридже Эндрю Уайлс наконец выступает с большой лекцией, в ходе которой он приводит обоснование гипотезы Таниямы и заявляет о доказательстве Великой теоремы Ферма.
Перед опубликованием в авторитетном математическом журнале, в соответствии с завещанием Пауля Вольфскеля, доказательство Уайлса объемом около двух сот страниц было поделено на шесть частей и передано на рецензирование различным ведущим математикам. И вскоре Ник Катц, один из рецензентов, в своей части доказательства Уайлса обнаруживает положение, которое не могло быть признано достаточно обоснованным. В результате представленное доказательство гипотезы Таниямы уже не могло считаться корректным. Но Эндрю Уайлису за сравнительно короткое время при помощи своего бывшего аспиранта Ричарда Тейлора все же удается закрыть пробел в своем доказательстве и 23 октября 1994 года представить в журнал доработанный вариант доказательства на ста тридцати страницах.
После тщательной проверки скорректированное доказательство Уйлса было признано безупречным и в мае 1995 года официально опубликовано. При этом вызывает удивление, что доказательство Уйлса было признанно корректным без ответов на имеющиеся очевидные проблемы в этом доказательстве. Совершенно непонятно как можно было в ходе тщательной проверки доказательства не заметить отмеченных выше проблем. Иначе как мистикой все это не объяснить.
Еще в большей степени трудно объяснить, что Эндрю Уайлс, обосновавший только гипотезу Таниямы был признан автором доказательства Великой теоремы Ферма. Ведь очень хорошо известно, что любое правильное доказательство математической теоремы должно быть абсолютным относительно времени создания. Иначе говоря, не зависеть и признаваться в качестве доказательства независимо от времени получения. В случае с доказательством, предложенным Эндрю Уайлсем, это условие не выполняется. Действительно если бы Эндрю Уайлс доказал бы гипотезу Таниямы до получения Герхардом Фреем вывода о возможной связи гипотезы Таниямы с Великой теоремой Ферма, то был бы он признан автором доказательства Великой теоремы Ферма? Очевидно, что нет. С другой стороны, если кто-либо в будущем предложит доказательство гипотезы Таниямы отличное от доказательства Уайлса, то будет ли он считаться автором нового варианта доказательства Великой теоремы Ферма? Тоже очевидно, что нет. И вообще, разве мало было получено различных математических утверждений, которые необходимо было использовать для доказательства Великой теоремы Ферма? Авторы всех этих математических утверждений тоже доказали Великую теорему Ферма?
Если рассуждения Герхарда Фрея считать корректными, то автором доказательства Великой теоремы Ферма логичнее было бы признать именно его, возможно в соавторстве с Кеном Рибетом.
Отмеченные проблемы в доказательстве Фрея - Рибета - Уайлса столь элементарны, что для того чтобы их понять, вовсе не надо быть профессиональным математиком. Поэтому совершенно непонятно чем все это можно объяснить?
Правда существуют утверждения, что современная математика вступила в эру слишком сложных, малопонятных большинству математиков доказательств. Доказательство Уайлса не стало исключением, действительно оно очень объемно и слишком сложно для понимания и, к сожалению явно не является тем чудесным доказательством, о котором говорил Пьер де Ферма. В связи с этим требовалось согласие математического сообщества с тем, что теорема на самом деле доказана.
В случае доказательства Великой теоремы Ферма, представленного Уайлсом, лишь совсем небольшое число специалистов по теории чисел признавали, что полностью понимают его рассуждения, а остальные просто сочли доказательство правильным. Те, кто не смог до конца понять доказательства, приняли его потому, что доказательство признали другие-те, кто все понял, и не захотели тратить свое время на то чтобы шаг за шагом проследить весь ход доказательства и проверить каждую деталь. При этом трудно сказать, сколько из тех немногих специалистов, которые считали, что полностью поняли доказательство, искренне не заблуждались на этот счет. Ведь даже при рецензировании текст доказательства был поделен на части, и каждый рецензент проверял только свою часть доказательства и не воспринимал его целиком.
И есть еще один вопрос. Рецензенты проверяли доказательство Великой теоремы Ферма или гипотезы Таниямы? Судя по всему, все же проверяли доказательство гипотезы Таниямы. А кто же тогда проверял доказательство Великой теоремы Ферма? Это обстоятельство отчасти способно объяснить существование отмеченных проблем доказательства Уайлса.
Однако ссылки на большие объемы и сложность современных доказательств не всегда оправданы. В большинстве случаев доказательства могут быть поделены на части, каждая из которых будет представлять собой совершенно самостоятельную теорему. Так, например, в состав доказательства Великой теоремы Ферма вовсе нет никакой необходимости включать доказательство гипотезы Таниямы, так как она является самостоятельной теоремой и может использоваться в ходе доказательства Великой теоремы Ферма наряду с другими существующими математическими утверждениями.
сентябрь 2005 года
![[]](/img/b/below_a_m/ab13/kniga.jpg) |
Теперь вся информация по альтернативной историиВеликой
теоремы Ферма собрана в одной книге: Андрей
Белов 'Великая мистификация Ферма' LAP
LAMBERT Academic Publishing (2017-03-14) ISBN-13:
978-3-659-79304-2 ISBN-10:
3659793043 EAN: 9783659793042 Приобрести книгу можно через интернет магазин Люблю Книги (www.ljubljuknigi.ru)
|
|